JAVA之单源最短路径（Single Source Shortest Path，SSSP问题）dijkstra算法求解

题目简介：给定一个带权有向图，再给定图中一个顶点（源点），求该点到其他所有点的最短距离，称为单源最短路径问题。

如下图，求点1到其他各点的最短距离

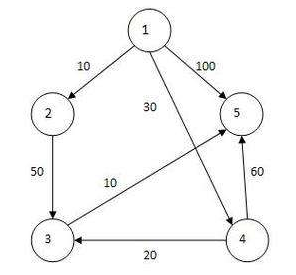
准备工作：以下为该题所需要用到的数据

int N; //保存顶点个数

int M; //保存边个数

int max; //用来设定一个比所有边的权都大的值，来表示两点间没有连线

int[] visit; //找到一个顶点的最短距离，就把它设为1，默认为0（即还没有找到）

int[][] distance; //保存图中个边的值，两点间无边则设为max

int[] bestmin;  //保存源点到其他各点的最短距离，用于最后输出

String[] path;  //有些题目会要求输出路径，保存输出路径

算法步骤：

①找出与源点距离最短的那个点，即遍历distance[1][1]，distance[1][2],.....distance[1][N]中的最小值，如题：

源点1到2,4,5的距离分别为10,30,100,。3无法直接到达即此时distance[1][3] = max。那么这一步找出的点就是

顶点2。此时distance[1][2]即为源点1到顶点2的最短距离。将visit[2]设为1（顶点2完成）。

②松弛操作，

以①找出的点作为中心点（此时为顶点2），去遍历visit[i]为0的点，如果distance[1][2] + distance[2][i] < distance[1][i]

就把新的较短路径赋值给它，即distance[1][i] = distance[1][2] + distance[2][i]，

此时顶点2能到达的点只有顶点3，并且distance[1][3] = max ，所以更新distance[1][3]的值为distance[1][2] + distance[2][3] = 60

完成以上两个步骤后回到步骤①，即这是个循环，每次循环能找出一个最短距离的点和更新其他点，所以该循环要遍历

N-1次就可以把所有点最短距离找出，大概过程如下：

for(int i = 2; i <= N; i++) {

　　步骤①（在一个循环内找到距离最短的点）

　　步骤②（以①找到的点为中心，通过一个循环更新所有visit[i]为0的点到源点的距离）

}

完整代码如下：

package algorithm;
import java.util.Scanner;
public class Dijkstra__Single_Source_Shortest_Path {

    private static int N;
    private static int M;
    private static int max;
    private static int[] visit;
    private static int[][] distance;
    private static int[] bestmin;
    private static String[] path;

    public static void Dijkstra() {
        visit[1] = 1;
        bestmin[1] = 0;

        //大循环（搞定这里就算搞定该算法了，后面的输出什么的可以不看）
        for(int l = 2; l <= N; l++) {
            int Dtemp = max;
            int k = -1;

            //步骤①
            for(int i = 2; i <= N; i++) {
                if(visit[i] == 0 && distance[1][i] < Dtemp) {
                    Dtemp = distance[1][i];
                    k = i;
                }
            }
            visit[k] = 1;
            bestmin[k] = Dtemp;

            //步骤②
            for(int i = 2; i <= N; i++) {
                if(visit[i] == 0 && (distance[1][k] + distance[k][i]) < distance[1][i]) {
                    distance[1][i] = distance[1][k] + distance[k][i];
                    path[i] = path[k] + "-->" + i;
                }
            }
        }

        //输出路径
        for(int i=1;i<=N;i++) {
             System.out.println("从"+1+"出发到"+i+"的最短路径为："+path[i]);
        }
        System.out.println("=====================================");
        for(int i = 1; i <= N; i++) {
            System.out.println("从1出发到" + i + "点的最短距离为：" + bestmin[i]);
        }
    }
    public static void main(String[] args) {
        // TODO Auto-generated method stub

        Scanner input = new Scanner(System.in);
        System.out.print("请输入节点个数N，路径总数M： ");
        N = input.nextInt();
        M = input.nextInt();
        max = 10000;
        bestmin = new int[N+1];
        distance = new int [N+1][N+1];
        visit = new int[N+1];
        path=new String[N+1];

        for(int i = 1; i <= N; i++) {
            for(int j = 1; j <= N; j++) {
                if(i == j) {
                    distance[i][j] = 0;
                }else {
                    distance[i][j] = max;
                }
            }
            bestmin[i] = max;
            path[i] = new String("1-->" + i);
        }

        System.out.println("请输入" + M +"条数据x，y，z（表示x点到y点的距离为z）：");
        for(int i = 1; i <= M; i++) {
            int x = input.nextInt();
            int y = input.nextInt();
            int z = input.nextInt();
            distance[x][y] = z;
        }
        input.close();

        Dijkstra();
    }

}

运行结果如下：