O(n*logn)级别的算法之一(归并排序及其优化)
原理:
设两个有序的子序列(相当于输入序列)放在同一序列中相邻的位置上:array[low..m],array[m + 1..high],先将它们合并到一个局部的暂存序列 temp (相当于输出序列)中,待合并完成后将 temp 复制回 array[low..high]中,从而完成排序。
在具体的合并过程中,设置 i,j 和 p 三个指针,其初值分别指向这三个记录区的起始位置。合并时依次比较 array[i] 和 array[j] 的关键字,取关键字较小(或较大)的记录复制到 temp[p] 中,然后将被复制记录的指针 i 或 j 加 1,以及指向复制位置的指针 p加 1。重复这一过程直至两个输入的子序列有一个已全部复制完毕(不妨称其为空),此时将另一非空的子序列中剩余记录依次复制到 array 中即可
备注:图片原理来源:https://blog.csdn.net/yinjiabin/article/details/8265827/
待排序列(14,12,15,13,11,16)
假设我们有一个没有排好序的序列,那么首先我们使用分割的办法将这个序列分割成一个个已经排好序的子序列。然后再利用归并的方法将一个个的子序列合并成排序好的序列。分割和归并的过程可以看下面的图例。
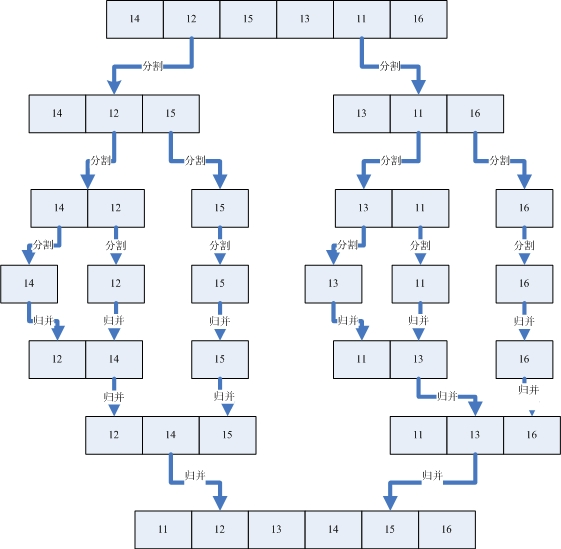
先"分割"再"合并"
从上图可以看出,我们首先把一个未排序的序列从中间分割成2部分,再把2部分分成4部分,依次分割下去,直到分割成一个一个的数据,再把这些数据两两归并到一起,使之有序,不停的归并,最后成为一个排好序的序列。
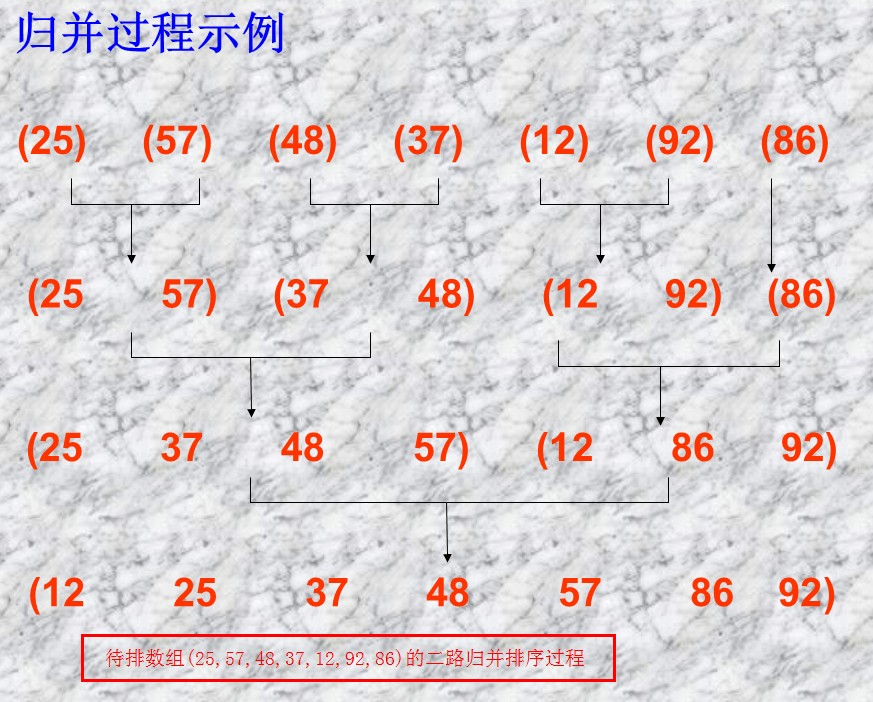
测试用例:
#ifndef INC_02_MERGE_SORT_SORTTESTHELPER_H
#define INC_02_MERGE_SORT_SORTTESTHELPER_H
#include <iostream>
#include <algorithm>
#include <string>
#include <ctime>
#include <cassert>
using namespace std;
namespace SortTestHelper {
// 生成有n个元素的随机数组,每个元素的随机范围为[rangeL, rangeR]
int *generateRandomArray(int n, int range_l, int range_r) {
int *arr = new int[n];
srand(time(NULL));
for (int i = ; i < n; i++)
arr[i] = rand() % (range_r - range_l + ) + range_l;
return arr;
}
// 生成一个近乎有序的数组
// 首先生成一个含有[0...n-1]的完全有序数组, 之后随机交换swapTimes对数据
// swapTimes定义了数组的无序程度
int *generateNearlyOrderedArray(int n, int swapTimes){
int *arr = new int[n];
for(int i = ; i < n ; i ++ )
arr[i] = i;
srand(time(NULL));
for( int i = ; i < swapTimes ; i ++ ){
int posx = rand()%n;
int posy = rand()%n;
swap( arr[posx] , arr[posy] );
}
return arr;
}
// 拷贝整型数组a中的所有元素到一个新的数组, 并返回新的数组
int *copyIntArray(int a[], int n){
int *arr = new int[n];
//* 在VS中, copy函数被认为是不安全的, 请大家手动写一遍for循环:)
copy(a, a+n, arr);
return arr;
}
// 打印arr数组的所有内容
template<typename T>
void printArray(T arr[], int n) {
for (int i = ; i < n; i++)
cout << arr[i] << " ";
cout << endl;
return;
}
// 判断arr数组是否有序
template<typename T>
bool isSorted(T arr[], int n) {
for (int i = ; i < n - ; i++)
if (arr[i] > arr[i + ])
return false;
return true;
}
// 测试sort排序算法排序arr数组所得到结果的正确性和算法运行时间
template<typename T>
void testSort(const string &sortName, void (*sort)(T[], int), T arr[], int n) {
clock_t startTime = clock();
sort(arr, n);
clock_t endTime = clock();
cout << sortName << " : " << double(endTime - startTime) / CLOCKS_PER_SEC << " s"<<endl;
assert(isSorted(arr, n));
return;
}
};
#endif //INC_02_MERGE_SORT_SORTTESTHELPER_H
插入排序(因为等下优化时需要用到):
#ifndef INC_03_MERGE_SORT_ADVANCE_INSERTIONSORT_H
#define INC_03_MERGE_SORT_ADVANCE_INSERTIONSORT_H
#include <iostream>
#include <algorithm>
using namespace std;
template<typename T>
void insertionSort(T arr[], int n){
for( int i = ; i < n ; i ++ ) {
T e = arr[i];
int j;
for (j = i; j > && arr[j-] > e; j--)
arr[j] = arr[j-];
arr[j] = e;
}
return;
}
// 对arr[l...r]范围的数组进行插入排序
template<typename T>
void insertionSort(T arr[], int l, int r){
for( int i = l+ ; i <= r ; i ++ ) {
T e = arr[i];
int j;
for (j = i; j > l && arr[j-] > e; j--)
arr[j] = arr[j-];
arr[j] = e;
}
return;
}
#endif //INC_03_MERGE_SORT_ADVANCE_INSERTIONSORT_H
一般归并排序:
#ifndef INC_03_MERGE_SORT_ADVANCE_MERGESORT_H
#define INC_03_MERGE_SORT_ADVANCE_MERGESORT_H
#include <iostream>
using namespace std;
// 将arr[l...mid]和arr[mid+1...r]两部分进行归并
template<typename T>
void __merge(T arr[], int l, int mid, int r){
T aux[r-l+];
for( int i = l ; i <= r; i ++ )
aux[i-l] = arr[i];
// 初始化,i指向左半部分的起始索引位置l;j指向右半部分起始索引位置mid+1
int i = l, j = mid+;
for( int k = l ; k <= r; k ++ ){
if( i > mid ){ // 如果左半部分元素已经全部处理完毕
arr[k] = aux[j-l]; j ++;
}
else if( j > r ){ // 如果右半部分元素已经全部处理完毕
arr[k] = aux[i-l]; i ++;
}
else if( aux[i-l] < aux[j-l] ) { // 左半部分所指元素 < 右半部分所指元素
arr[k] = aux[i-l]; i ++;
}
else{ // 左半部分所指元素 >= 右半部分所指元素
arr[k] = aux[j-l]; j ++;
}
}
}
// 递归使用归并排序,对arr[l...r]的范围进行排序
template<typename T>
void __mergeSort(T arr[], int l, int r){
if( l >= r )
return;
int mid = (l+r)/;
__mergeSort(arr, l, mid);
__mergeSort(arr, mid+, r);
__merge(arr, l, mid, r);
}
template<typename T>
void mergeSort(T arr[], int n){
__mergeSort( arr , , n- );
}
#endif //INC_03_MERGE_SORT_ADVANCE_MERGESORT_H
优化后的归并排序:
#include <iostream>
#include "SortTestHelper.h"
#include "InsertionSort.h"
#include "MergeSort.h"
using namespace std;
// 使用优化的归并排序算法, 对arr[l...r]的范围进行排序
template<typename T>
void __mergeSort2(T arr[], int l, int r){
// 优化2: 对于小规模数组, 使用插入排序
if( r - l <= ){
insertionSort(arr, l, r);
return;
}
int mid = (l+r)/;
__mergeSort2(arr, l, mid);
__mergeSort2(arr, mid+, r);
// 优化1: 对于arr[mid] <= arr[mid+1]的情况,不进行merge
// 对于近乎有序的数组非常有效,但是对于一般情况,有一定的性能损失
if( arr[mid] > arr[mid+] )
__merge(arr, l, mid, r);
}
template<typename T>
void mergeSort2(T arr[], int n){
__mergeSort2( arr , , n- );
}
int main() {
int n = ;
// 测试1 一般性测试
cout<<"Test for random array, size = "<<n<<", random range [0, "<<n<<"]"<<endl;
int* arr1 = SortTestHelper::generateRandomArray (n,,n);
int* arr2 = SortTestHelper::copyIntArray(arr1, n);
int* arr3 = SortTestHelper::copyIntArray(arr1, n);
SortTestHelper::testSort("Insertion Sort", insertionSort, arr1, n);
SortTestHelper::testSort("Merge Sort", mergeSort, arr2, n);
SortTestHelper::testSort("Merge Sort 2", mergeSort2, arr3, n);
delete[] arr1;
delete[] arr2;
delete[] arr3;
cout<<endl;
// 测试2 测试近乎有序的数组
int swapTimes = ;
assert( swapTimes >= );
cout<<"Test for nearly ordered array, size = "<<n<<", swap time = "<<swapTimes<<endl;
arr1 = SortTestHelper::generateNearlyOrderedArray(n,swapTimes);
arr2 = SortTestHelper::copyIntArray(arr1, n);
arr3 = SortTestHelper::copyIntArray(arr1, n);
SortTestHelper::testSort("Insertion Sort", insertionSort, arr1, n);
SortTestHelper::testSort("Merge Sort", mergeSort, arr2, n);
SortTestHelper::testSort("Merge Sort 2", mergeSort2, arr3, n);
delete[] arr1;
delete[] arr2;
delete[] arr3;
return ;
}
测试结果:
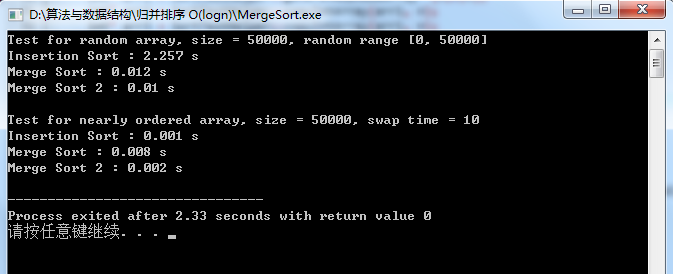
O(n*logn)级别的算法之一(归并排序及其优化)的更多相关文章
- O(n*logn)级别的算法之二(快速排序)的三种实现方法详解及其与归并排序的对比
一,单路快排1.测试用例: #ifndef INC_06_QUICK_SORT_DEAL_WITH_NEARLY_ORDERED_ARRAY_SORTTESTHELPER_H #define INC_ ...
- 排序算法之归并排序(Mergesort)解析
转自:http://www.cnblogs.com/ayqy/p/4050452.html 一.归并排序的优缺点(pros and cons) 耗费心思来理解它,总要有个理由吧: 归并排序的效率达 ...
- Java常见排序算法之归并排序
在学习算法的过程中,我们难免会接触很多和排序相关的算法.总而言之,对于任何编程人员来说,基本的排序算法是必须要掌握的. 从今天开始,我们将要进行基本的排序算法的讲解.Are you ready?Let ...
- 【DS】排序算法之归并排序(Merge Sort)
一.算法思想 归并排序是建立在归并操作上的一种有效的排序算法.该算法是采用分治法的一个非常典型的应用,指的是将两个已经排序的序列合并成一个序列的操作.其归并思想如下: 1)申请空间,使其大小为两个已经 ...
- Python排序搜索基本算法之归并排序实例分析
Python排序搜索基本算法之归并排序实例分析 本文实例讲述了Python排序搜索基本算法之归并排序.分享给大家供大家参考,具体如下: 归并排序最令人兴奋的特点是:不论输入是什么样的,它对N个元素的序 ...
- 归并排序及优化(Java实现)
普通归并排序 public class MergeSort { /** * @param arr 待排序的数组 * @param left 本次归并的左边界 * @param mid 本次归并的中间位 ...
- 谷歌蜂鸟算法对网站seo优化有何影响
http://www.wocaoseo.com/thread-89-1-1.html 谷歌在过去三个月里,非常低调的推出了蜂鸟算法,据谷歌技术员表示,此种方法一出,将影响90%网站的排名, ...
- 用Java写算法之归并排序
转自:http://flyingcat2013.blog.51cto.com/7061638/1281026 前面的三种排序算法(冒泡排序,选择排序,插入排序)在平均情况下均为O(n^2)复杂度,在处 ...
- o(1), o(n), o(logn), o(nlogn)算法复杂度
在描述算法复杂度时,经常用到o(1), o(n), o(logn), o(nlogn)来表示对应算法的时间复杂度, 这里进行归纳一下它们代表的含义: 这是算法的时空复杂度的表示.不仅仅用于表示时间复杂 ...
随机推荐
- 先序遍历DOM树的5种方法
DOM树由文档中的所有节点(元素节点.文本节点.注释节点等)所构成的一个树结构,DOM树的解析和构建是浏览器要实现的关键功能.既然DOM树是一个树结构,那么我们就可以使用遍历树结构的相关方法来对DOM ...
- Maven整合SSM测试
前面也说到了关于SSM的整合,话不多说直接从创建项目开始CRUD之路(参考前面写过的Mybatis和Spring整合,SSM简单整合),这是整个项目的结构 以及最终的结果.(附上下载地址) 一.创建M ...
- pip 安装模块时出现error: Microsoft Visual C++ 14.0 is required. Get it with "Microsoft Visual C++ Build Tools":
在使用pip安装mysqlclient模块时,出现如下错误: 在网上查找资料后显示可能是由于不兼容导致的,最好去下载.whl文件安装成功. 资源地址:http://www.lfd.uci.edu/~g ...
- 一条SQL语句在MySQL中如何执行的
本篇文章会分析一个 sql 语句在 MySQL 中的执行流程,包括 sql 的查询在 MySQL 内部会怎么流转,sql 语句的更新是怎么完成的. 在分析之前我会先带着你看看 MySQL 的基础架构, ...
- Matplotlib 使用 - 《Python 数据科学手册》学习笔记
一.引入 import matplotlib as mpl import matplotlib.pyplot as plt 二.配置 1.画图接口 Matplotlib 有两种画图接口: (1)一个是 ...
- yarn组件通信协议简介
ResourceManager与NodeManager通过ResourceTracker协议通信. NodeManager通过NodeStatusUpdaterImpl中的ResourceTracke ...
- ionic 热更新 cordova-hot-code-push
cordova-hot-code-push ,Cordova热代码推送插件提供了在应用程序中执行基于Web的内容的自动更新的功能.使用此插件可以更新存储在项目的www文件夹中的所有内容. cordov ...
- 课程回顾-Convolutional Neural Networks
为什么卷积层计算量更低paddingStrided convolution多维卷积LeNet 参数卷积网络的好处参数共享稀疏连接经典网络实现LeNet-5AlexNetVGGResNet残差块iden ...
- mysql 开发进阶篇系列 13 锁问题(关于表锁,死锁示例,锁等待设置)
一. 什么时候使用表锁 对于INNODB表,在绝大部分情况下都应该使用行锁.在个别特殊事务中,可以考虑使用表锁(建议). 1. 事务需要更新大部份或全部数据,表又比较大,默认的行锁不仅使这个事务执行效 ...
- Java 容器 & 泛型:三、HashSet,TreeSet 和 LinkedHashSet比较
Writer:BYSocket(泥沙砖瓦浆木匠) 微博:BYSocket 豆瓣:BYSocket 上一篇总结了下ArrayList .LinkedList和Vector比较,今天泥瓦匠总结下Hash ...
