重新整理数据结构与算法(c#)——算法套路普利姆算法[二十九]
前言
看一个题目:
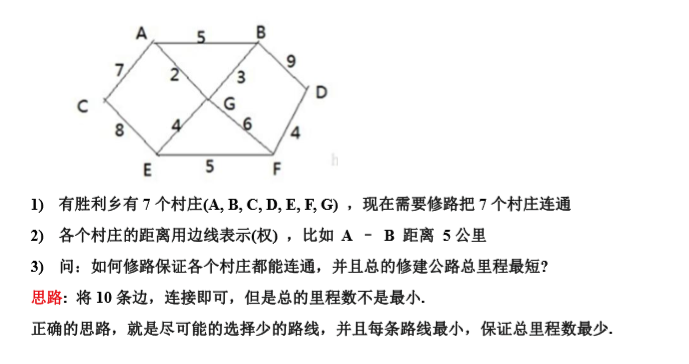
这个问题就是求最小生成树,是图转换为树的一种方式。
最小生成树概念:
最小生成树简称MST。
1.n个顶点,一定有n-1条边
2.包含全部顶点。
3.图转换为最小生成树,权重之和最小。
解题思路:
假设从a开始为顶点,找到和a相接的最小边。
在图中和a相接的是G,那么选择条。然后找到和A、G相接的最小边,是BG,然后选择BG这条边。
以此类推。
正文
代码:
static void Main(string[] args)
{
char[] data = new char[] { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
int verxs = data.Length;
//邻接矩阵的关系使用二维数组表示,10000这个大数,表示两个点不联通
int[,] weight = new int[,]{
{10000,5,7,10000,10000,10000,2},
{5,10000,10000,9,10000,10000,3},
{7,10000,10000,10000,8,10000,10000},
{10000,9,10000,10000,10000,4,10000},
{10000,10000,8,10000,10000,5,4},
{10000,10000,10000,4,5,10000,6},
{2,3,10000,10000,4,6,10000},};
//创建要修的路,初始化节点的个数
MGraph mGraph = new MGraph(verxs);
//创建一个MinTree对象
MinTree minTree = new MinTree();
minTree.createGraph(mGraph, verxs, data, weight);
Console.WriteLine("显示原始图");
minTree.showGraph(mGraph);
var newGraph=minTree.prim(mGraph, 0);
Console.WriteLine("显示最小生成树图");
minTree.showGraph(newGraph);
Console.Read();
}
}
class MinTree {
//不污染数据
public void createGraph(MGraph mGraph, int verxs, char[] data, int[,] weight)
{
for (int i = 0; i < verxs; i++)
{
mGraph.data[i] = data[i];
for (int j = 0; j < verxs; j++)
{
mGraph.weight[i,j] = weight[i,j];
}
}
}
//遍历图
public void showGraph(MGraph mGraph)
{
for (int i=0;i<mGraph.verxs;i++)
{
for (int j = 0; j < mGraph.verxs; j++)
{
Console.Write(mGraph.weight[i,j]+" ");
}
Console.WriteLine();
}
}
/// <summary>
/// 图转树核心算法
/// </summary>
/// <param name="mGraph">原始图</param>
/// <param name="v">初始化访问节点</param>
public MGraph prim(MGraph mGraph,int v)
{
int[] isVisited = new int[mGraph.verxs];
isVisited[v] = 1;
int y = -1;//y为数组竖轴
int x = -1;//x为数组横轴
MGraph newGraph = new MGraph(mGraph.verxs);
newGraph.data = (char[])mGraph.data.Clone();
int minWeight = 1000;
//一共要计算出verxs-1条边
for (int k=1;k<mGraph.verxs;k++)
{
for (int i=0;i<mGraph.verxs;i++)
{
for (int j = 0; j < mGraph.verxs ; j++)
{
if (isVisited[i] == 1 && isVisited[j] == 0 && mGraph.weight[i, j] < minWeight)
{
y = i;
x = j;
minWeight = mGraph.weight[i, j];
}
}
}
Console.WriteLine("在"+mGraph.data[y]+"和"+ mGraph.data[x]+"之间修了一条权重为"+minWeight+"的路");
newGraph.weight[y,x] = minWeight;
isVisited[x] = 1;
minWeight = 1000;
}
return newGraph;
}
}
结果:
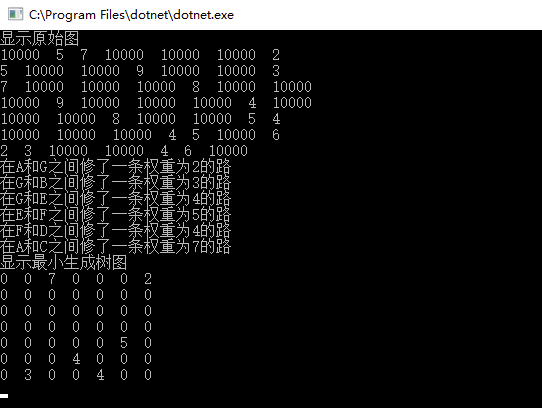
重新整理数据结构与算法(c#)——算法套路普利姆算法[二十九]的更多相关文章
- 最小生成树-普利姆算法eager实现
算法描述 在普利姆算法的lazy实现中,参考:普利姆算法的lazy实现 我们现在来考虑这样一个问题: 我们将所有的边都加入了优先队列,但事实上,我们真的需要所有的边吗? 我们再回到普利姆算法的lazy ...
- 最小生成树-普利姆算法lazy实现
算法描述 lazy普利姆算法的步骤: 1.从源点s出发,遍历它的邻接表s.Adj,将所有邻接的边(crossing edges)加入优先队列Q: 2.从Q出队最轻边,将此边加入MST. 3.考察此边的 ...
- 普利姆算法(prim)
普利姆算法(prim)求最小生成树(MST)过程详解 (原网址) 1 2 3 4 5 6 7 分步阅读 生活中最小生成树的应用十分广泛,比如:要连通n个城市需要n-1条边线路,那么怎么样建设才能使工程 ...
- 算法与数据结构(五) 普利姆与克鲁斯卡尔的最小生成树(Swift版)
上篇博客我们聊了图的物理存储结构邻接矩阵和邻接链表,然后在此基础上给出了图的深度优先搜索和广度优先搜索.本篇博客就在上一篇博客的基础上进行延伸,也是关于图的.今天博客中主要介绍两种算法,都是关于最小生 ...
- HDU 1879 继续畅通工程 (Prim(普里姆算法)+Kruskal(克鲁斯卡尔))
继续畅通工程 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Sub ...
- 最小生成树-普利姆(Prim)算法
最小生成树-普利姆(Prim)算法 最小生成树 概念:将给出的所有点连接起来(即从一个点可到任意一个点),且连接路径之和最小的图叫最小生成树.最小生成树属于一种树形结构(树形结构是一种特殊的图),或者 ...
- 图论---最小生成树----普利姆(Prim)算法
普利姆(Prim)算法 1. 最小生成树(又名:最小权重生成树) 概念:将给出的所有点连接起来(即从一个点可到任意一个点),且连接路径之和最小的图叫最小生成树.最小生成树属于一种树形结构(树形结构是一 ...
- 查找最小生成树:普里姆算法算法(Prim)算法
一.算法介绍 普里姆算法(Prim's algorithm),图论中的一种算法,可在加权连通图里搜索最小生成树.意即由此算法搜索到的边子集所构成的树中,不但包括了连通图里的所有顶点,且其所有边的权值之 ...
- hdu 1233:还是畅通工程(数据结构,图,最小生成树,普里姆(Prim)算法)
还是畅通工程 Time Limit : 4000/2000ms (Java/Other) Memory Limit : 65536/32768K (Java/Other) Total Submis ...
- c/c++ 用普利姆(prim)算法构造最小生成树
c/c++ 用普利姆(prim)算法构造最小生成树 最小生成树(Minimum Cost Spanning Tree)的概念: 假设要在n个城市之间建立公路,则连通n个城市只需要n-1条线路.这时 ...
随机推荐
- 替换掉Chrome浏览器的新标签页【已做好自己的插件,并提供下载】
https://jingyan.baidu.com/article/fc07f9891b256312ffe5190a.html 我做好了自己的 Chrome 新插件 https://files.cnb ...
- SPEAK 510全向麦克风无线蓝牙拾音器产品体验及评测
产品简介 大家开会的时候,很多人都直接使用手机app了,比如,zoom,腾讯会议等.既方便又快捷.由于手机设备拾音距离有限,也不是针对会议场景做的,所有,在多人会议的时候,问题就出来了.这个时 ...
- JS(循环)
一 for循环 在程序中,一组被重复执行的语句被称之为循环体,能否继续重复执行,取决于循环的终止条件.由循环体及循环的终止条件组成的语句,被 称之为循环语句 1 语法结构 for循环主要用于把某些代码 ...
- 三维模型OBJ格式轻量化压缩在移动智能终端应用方面的重要性分析
三维模型OBJ格式轻量化压缩在移动智能终端应用方面的重要性分析 三维模型的OBJ格式轻量化压缩在移动智能终端应用方面具有重要性.以下是对三维模型OBJ格式轻量化压缩在移动智能终端应用方面重要性的分析: ...
- 探讨三维模型OBJ格式轻量化在三维展示效果上的重要性
探讨三维模型OBJ格式轻量化在三维展示效果上的重要性 三维模型的OBJ格式轻量化在三维展示效果方面具有重要性.以下是对三维模型OBJ格式轻量化在三维展示效果上的重要性进行分析: 1.提高渲染性能:原始 ...
- 记录--手把手教你,用electron实现截图软件
这里给大家分享我在网上总结出来的一些知识,希望对大家有所帮助 背景 因为我们日常开发项目的时候,需要和同事对接api和文档还有UI图,所以有时候要同时打开多个窗口,并在多个窗口中切换,来选择自己要的信 ...
- 补充--关于nginx服务器多个网站如何设置404的问题?
补充--关于nginx服务器多个网站如何设置404的问题? 需求1 :设置多个网站404页面为一个 都需配置网站的nginx.conf,以上面的多网站为例,404发布目录下,每个的nginx.conf ...
- Oracle 已存在数据的大表 改 分区表
创建表,插入测试数据 -- Create table create table LXW_TEST ( CDATE DATE, T1 NUMBER, T2 VARCHAR2(2) ) ; insert ...
- java 计算两个日期相差工作日天数
import java.text.ParseException; import java.text.SimpleDateFormat; import java.time.DayOfWeek; impo ...
- 在使用若依分离版时遇到富文本不显示html解决
<el-table-column label="公告内容" align="center" prop="content"> < ...
