A - 小希的迷宫

来源 hdu1272

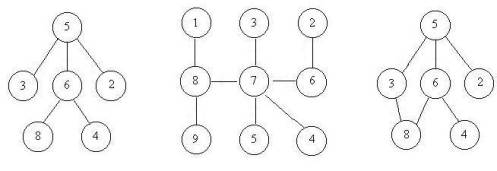
上次Gardon的迷宫城堡小希玩了很久（见Problem B），现在她也想设计一个迷宫让Gardon来走。但是她设计迷宫的思路不一样，首先她认为所有的通道都应该是双向连通的，就是说如果有一个通道连通了房间A和B，那么既可以通过它从房间A走到房间B，也可以通过它从房间B走到房间A，为了提高难度，小希希望任意两个房间有且仅有一条路径可以相通（除非走了回头路）。小希现在把她的设计图给你，让你帮忙判断她的设计图是否符合她的设计思路。比如下面的例子，前两个是符合条件的，但是最后一个却有两种方法从5到达8。

Input

输入包含多组数据，每组数据是一个以0 0结尾的整数对列表，表示了一条通道连接的两个房间的编号。房间的编号至少为1，且不超过100000。每两组数据之间有一个空行。

整个文件以两个-1结尾。

Output

对于输入的每一组数据，输出仅包括一行。如果该迷宫符合小希的思路，那么输出"Yes"，否则输出"No"。

Sample Input

6 8 5 3 5 2 6 4

5 6 0 0

8 1 7 3 6 2 8 9 7 5

7 4 7 8 7 6 0 0

3 8 6 8 6 4

5 3 5 6 5 2 0 0

-1 -1

Sample Output

Yes

Yes

No

有两种情况是No的，第一种是如果出现的两个点的祖宗是同一个人，那么说明之前已经有成一串了，在连就会变成环，NO；第二种比较坑，就是出现的可能是两个独立的串，这种要判断有多少个独立的串超过两个就是No；

#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include <iomanip>
#include<cmath>
#include<float.h>
#include<string.h>
#include<algorithm>
#define sf scanf
#define pf printf
#define mm(x,b) memset((x),(b),sizeof(x))
#include<vector>
#include<queue>
#include<stack>
#include<map>
#define rep(i,a,n) for (int i=a;i<n;i++)
#define per(i,a,n) for (int i=a;i>=n;i--)
typedef long long ll;
const ll mod=1e9+100;
const double eps=1e-8;
using namespace std;
const double pi=acos(-1.0);
const int inf=0xfffffff;
int pre[100005],temp,visit[100005];
int find(int x)
{
	if(pre[x]==x) return x;
	return pre[x]=find(pre[x]);
}
void Union(int x,int y)
{
	int a=find(x),b=find(y);
	if(a==b)
	{
		temp=1;return ;
	}
	pre[a]=b;
}
int main()
{
	while(1)
	{
		mm(visit,0);
		rep(i,0,100005) pre[i]=i;
		int x,y;
		temp=0;
		int sum=0;
		while(1)
		{
			sf("%d%d",&x,&y);
			if(x+y==0) break;
			else if(x==-1&&y==-1) return 0;
			Union(x,y);
			visit[x]=1;visit[y]=1;
		}
		rep(i,0,100005) if(visit[i]&&pre[i]==i) sum++; //判断是否超过两个独立的
		if(temp||sum>1) pf("No\n");
		else pf("Yes\n");
	}
}