转载请注明出处：

http://www.cnblogs.com/darkknightzh/p/9043395.html

参考网址：

https://github.com/deepinsight/insightface/blob/master/src/align/align_megaface.py中IOU的计算。

理解不对的地方敬请谅解。

IOU是两个矩形的交集与两个矩形并集的比值（可以这样理解吧）。

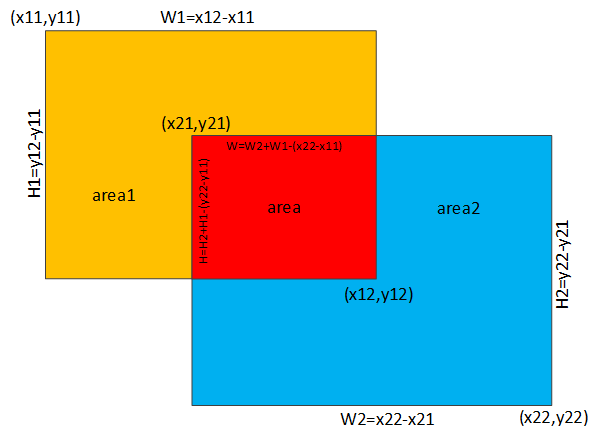
如下图所示：

黄色矩形起点坐标(x11,y11)，终点坐标(x12,y12)

蓝色矩形起点坐标(x21,y21)，终点坐标(x22,y22)。

则：

黄色矩形宽W1=x12-x11，高H1=y12-y11

黄色矩形宽W2=x22-x21，高H1=y22-y21

两个矩形交集（红色矩形）宽W=W1+W2-(x22-x11)=x12-x11

两个矩形交集（红色矩形）高H=H1+H2-(y22-y11)=y12-y11

红色矩形面积（两个矩形交集）为area=W*H

两个矩形并集为area1+area2-area

如果x12<x21或者y12<y21，说明两个矩形无公共区域，IOU=0；

否则，IOU=area/(area1+area2-area)

（原）IOU的计算的更多相关文章

  1. vga显示原理即相关计算

    行扫描周期:完成一行扫描所需时间: 行时序时间(a,b,c,d,e):完成一个像素点显示得时间 场扫描周期:完成所有行(一帧扫描所需时间) 场时序时间(o,p,q,r,s):完成一行显示得时间,一个完 ...

  2. 目标检测——IoU 计算

    Iou 的计算 我们先考虑一维的情况:令 \(A = [x_1,x_2], B = [y_1, y_2]\),若想要 \(A\) 与 \(B\) 有交集,需要满足如下情况: 简言之,要保证 \(A\) ...

  3. 使用Python的yield实现流计算模式

    首先先提一下上一篇<如何猜出Y combinator>中用的方法太复杂了.其实在Lambda演算中实现递归的思想很简单,就是函数把自己作为第一个参数传入函数,然后后面就是简单的Lambda ...

  4. 原码 & 反码 & 补码 & 详解

    本篇文章讲解了计算机的原码, 反码和补码. 并且进行了深入探求了为何要使用反码和补码, 以及更进一步的论证了为何可以用反码, 补码的加法计算原码的减法. 论证部分如有不对的地方请各位牛人帮忙指正! 希 ...

  5. CRC（Cyclic Redundancy Check)循环冗余校验码与海明码的计算题

    (17)采用CRC进行差错校验,生成多项式为G(X)=X4+X+1,信息码字为10111,则计算出的CRC校验码是  (17)  .A．0000  B．0100   C．0010   D．1100试题 ...

  6. 原代码,反码,解释和具体的补充 Java在&gt;&gt;和&gt;&gt;&gt;差异

    前两天分析 HashMap 的 hash 算法的时间,会见 >> 和 >>> 这两个符号.然后检查以下信息,我脑子里在某一时刻.今天遇到,我没想到居然忘  0-0.... ...

  7. java 变量及数据类型、原码、反码、补码

    Java基础——变量及数据类型 变量的概念 内存中的一个存储区域 变量名+数据类型 可在同一类型范围内不断变化 为什么定义变量: 用于不断的存放同一类型的常量,并可以重复使用 使用变量注意: 变量的作 ...

  8. Java 原码 反码 补码

    本篇文章讲解了计算机的原码, 反码和补码. 并且进行了深入探求了为何要使用反码和补码, 以及更进一步的论证了为何可以用反码, 补码的加法计算原码的减法. 论证部分如有不对的地方请各位牛人帮忙指正! 希 ...

  9. 目标识别（object detection）中的 IoU（Intersection over Union）

    首先直观上来看 IoU 的计算公式: 由上述图示可知,IoU 的计算综合考虑了交集和并集,如何使得 IoU 最大,需要满足,更大的重叠区域,更小的不重叠的区域. 两个矩形窗格分别表示: 左上点.右下点 ...

随机推荐

  1. Github+阿超运算

    感谢自己寒假能够稍稍做一点努力. Github个人页面<构建之法阅读笔记二可见>: https://github.com/Heartxy8990 申请教程: http://jingyan. ...

  2. 图片裁切展示css

    .wen_photo{ overflow:hidden;}.wen_photo img{ margin:0; padding:0; width:100%; height: 100%; object-f ...

  3. docker使用dockerfile 构建redis镜像

    FROM redis WORKDIR /data VOLUME /data EXPOSE RUN echo "success---------success" ENTRYPOINT ...

  4. ubuntu安装nodejs出现./config.gypi错误

    报错的内容如下: xxx@xxx [/usr/local/src/node-v0.8.3]# ./configure { 'target_defaults': { 'cflags': [], 'def ...

  5. BASH if/while/until loop

    #/bin/bash ]; then counter=" counter1=" echo "for loop:" $); do echo $i done ); ...

  6. File类基本用法

    [例子1]创建一个新文件. import java.io.*; class hello{ public static void main(String[] args) { File f=new Fil ...

  7. Android-LruCache与DiskLruCache

    Android LruCache与DiskLruCache 学习自 Android开发艺术探索 https://blog.csdn.net/guolin_blog/article/details/28 ...

  8. Alpha冲刺随笔三：第三天

    课程名称:软件工程1916|W(福州大学) 作业要求:项目Alpha冲刺(十天冲刺) 团队名称:葫芦娃队 作业目标:在十天冲刺里对每天的任务进行总结. 随笔汇总:https://www.cnblogs ...

  9. {}+[]与console.log({}+[])结果不同？从JavaScript的大括号谈起

    看到这样一个问题:为什么直接在控制台运行{} + []和用console.log({} + [])输出,两者结果不一样? 于是乎打开chrome的控制台运行了一下: 为什么结果会这样呢?不得已学习一下 ...

  10. grpc使用客户端技巧

    grpc 使用技巧,最近在做的项目是服务端是go语言提供服务使用的是grpc框架. java在实现客户端的时候,参数的生成大部分采用创建者模式.java在接受go服务端 返回数据的时候,更多的是通过p ...