LeetCode 笔记系列 17 Largest Rectangle in Histogram

题目： Largest Rectangle in Histogram

Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

The largest rectangle is shown in the shaded area, which has area = 10 unit.

For example,
Given height = [2,1,5,6,2,3],
return 10.

解法一： 这样的题目一般都有O(n)的解法，因为O(n²)的解法实在是太显而易见了。

可悲的是，本娃就只写出了后者。。。代码如下：

 public int largestRectangleArea(int[] height) {
         // Start typing your Java solution below
         // DO NOT write main() function
         int[] min = new int[height.length];
         int maxArea = 0;
         for(int i = 0; i < height.length; i++){
             if(height[i] != 0 && maxArea/height[i] >= (height.length - i)) {
                 continue;
             }
             for(int j = i; j < height.length; j++){
                 if(i == j) min[j] = height[j];
                 else {
                     if(height[j] < min[j - 1]) {
                         min[j] = height[j];
                     }else min[j] = min[j-1];
                 }
                 int tentativeArea = min[j] * (j - i + 1);
                 if(tentativeArea > maxArea) {
                     maxArea = tentativeArea;
                 }
             }
         }
         return maxArea;
     }

基本思想就是遍历所有[i, j]，并在过程中找出中间最矮的bar，得出从i到j的矩形面积。

不过我就知道，一定有大神用他们极简的代码来切题，下面就是一个。

解法二：

 public int largestRectangleArea2(int[] height) {
         Stack<Integer> stack = new Stack<Integer>();
         int i = 0;
         int maxArea = 0;
         int[] h = new int[height.length + 1];
         h = Arrays.copyOf(height, height.length + 1);
         while(i < h.length){
             if(stack.isEmpty() || h[stack.peek()] <= h[i]){
                 stack.push(i++);
             }else {
                 int t = stack.pop();
                 maxArea = Math.max(maxArea, h[t] * (stack.isEmpty() ? i : i - stack.peek() - 1));
             }
         }
         return maxArea;
     }

16行，给跪了。。。。

这个我不去debug下都特么不知道在干嘛。

那要不就debug下看看这段代码在做神马。例子就用题目中的[2,1,5,6,2,3]吧。

首先，如果栈是空的，那么索引i入栈。那么第一个i=0就进去吧。注意栈内保存的是索引，不是高度。然后i++。

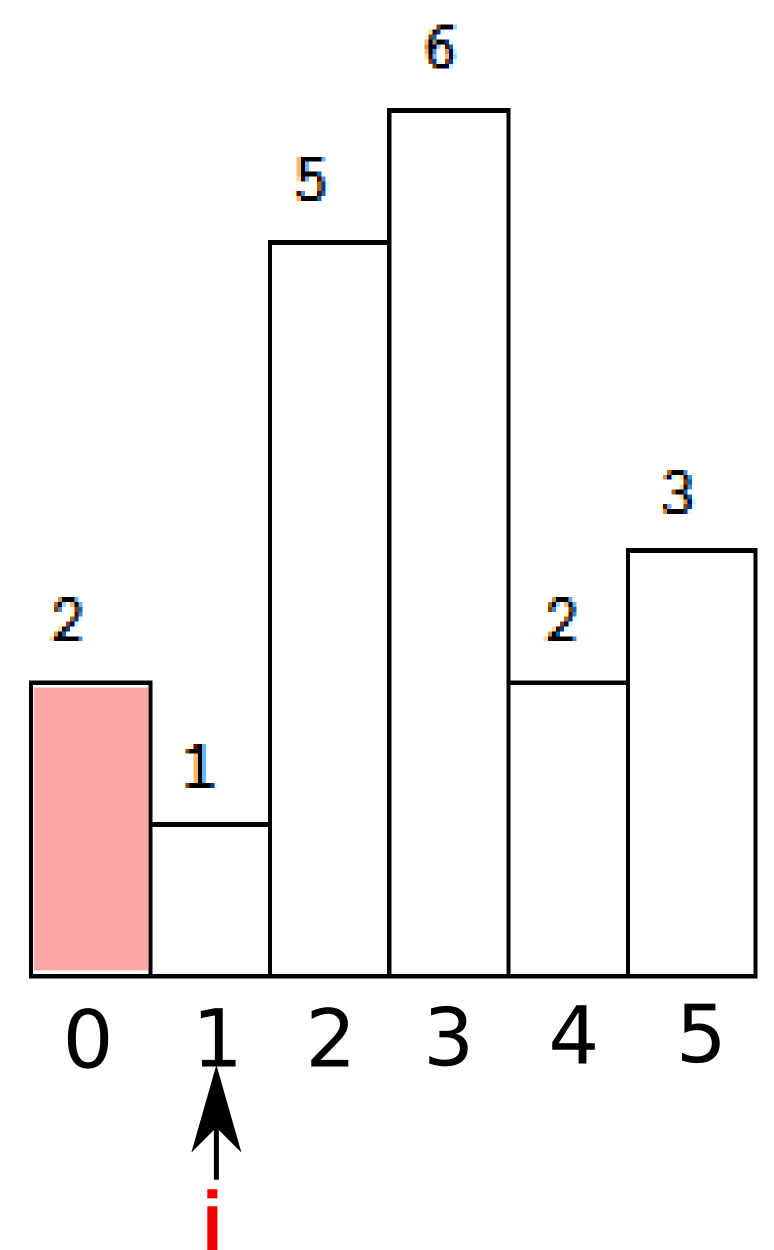
然后继续，当i=1的时候，发现h[i]小于了栈内的元素，于是出栈。（由此可以想到，哦，看来stack里面只存放单调递增的索引）

这时候stack为空，所以面积的计算是h[t] * i.t是刚刚弹出的stack顶元素。也就是蓝色部分的面积。

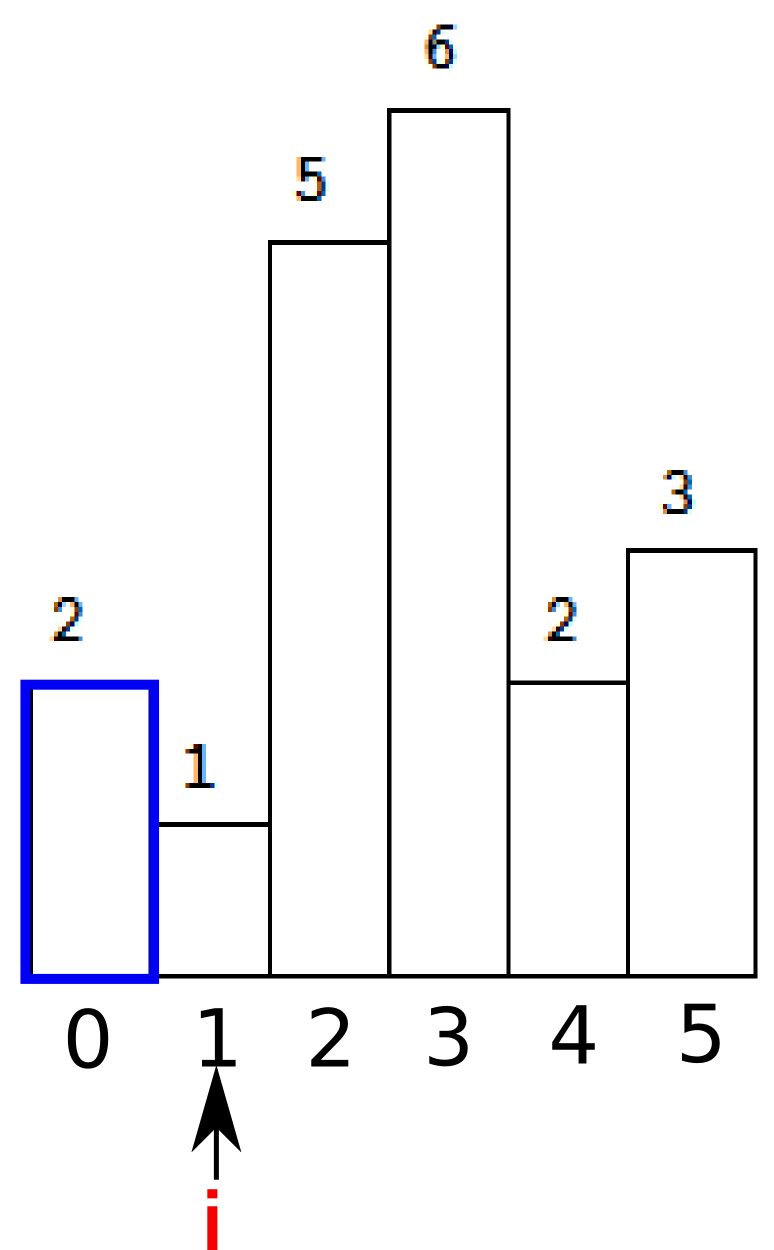
继续。这时候stack为空了，继续入栈。注意到只要是连续递增的序列，我们都要keep pushing，直到我们遇到了i=4，h[i]=2小于了栈顶的元素。

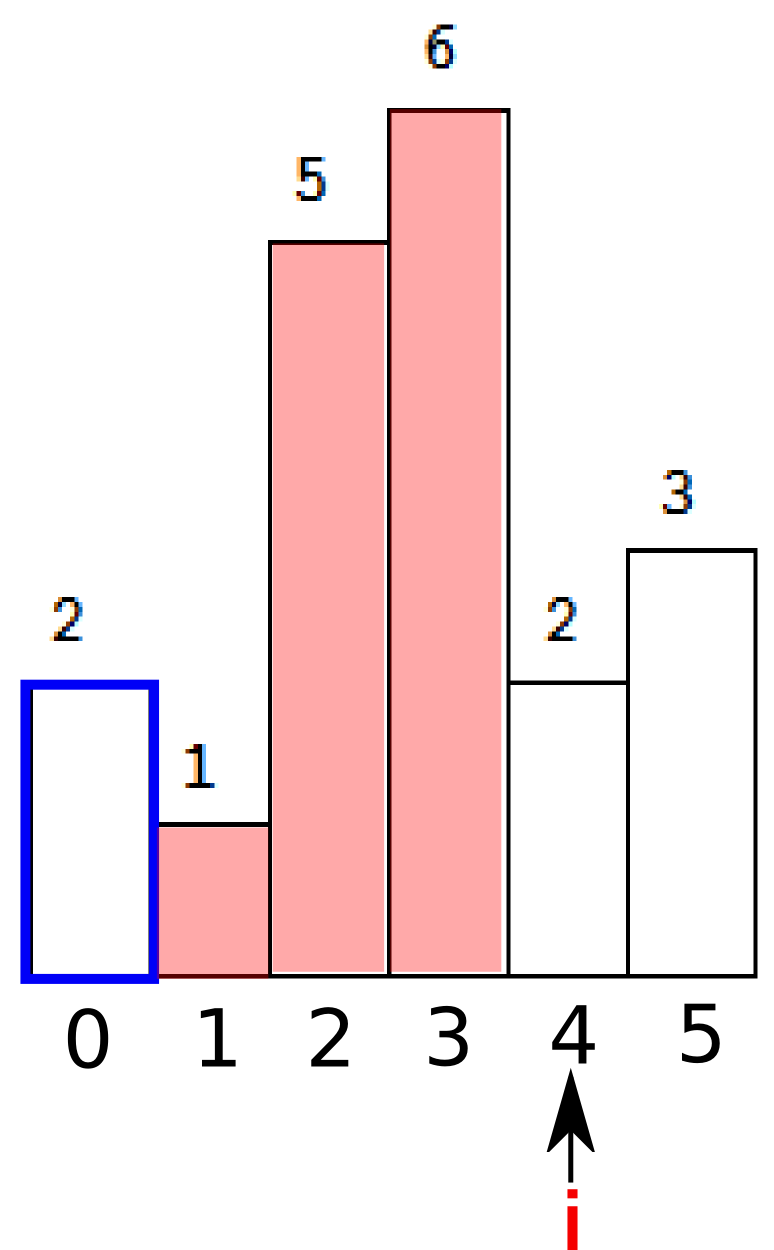
这时候开始计算矩形面积。首先弹出栈顶元素，t=3。即下图绿色部分。

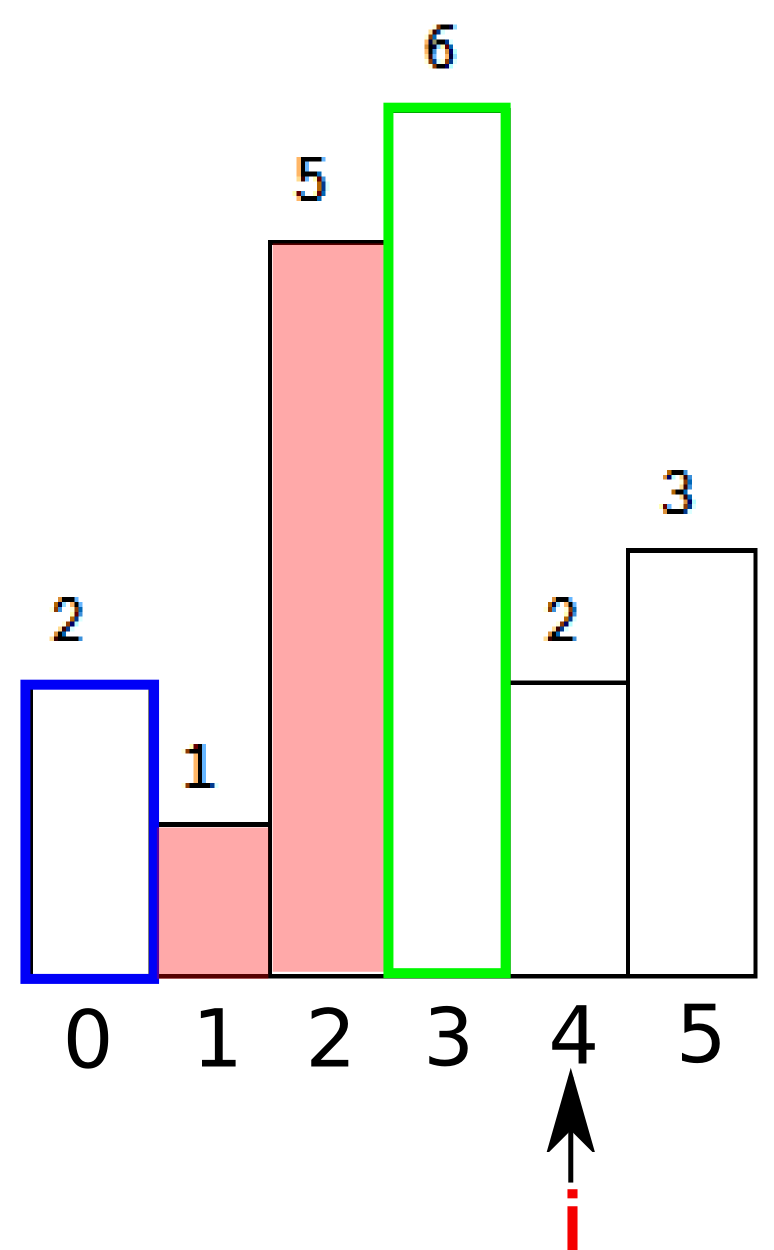
接下来注意到栈顶的（索引指向的）元素还是大于当前i指向的元素，于是出栈，并继续计算面积，桃红色部分。

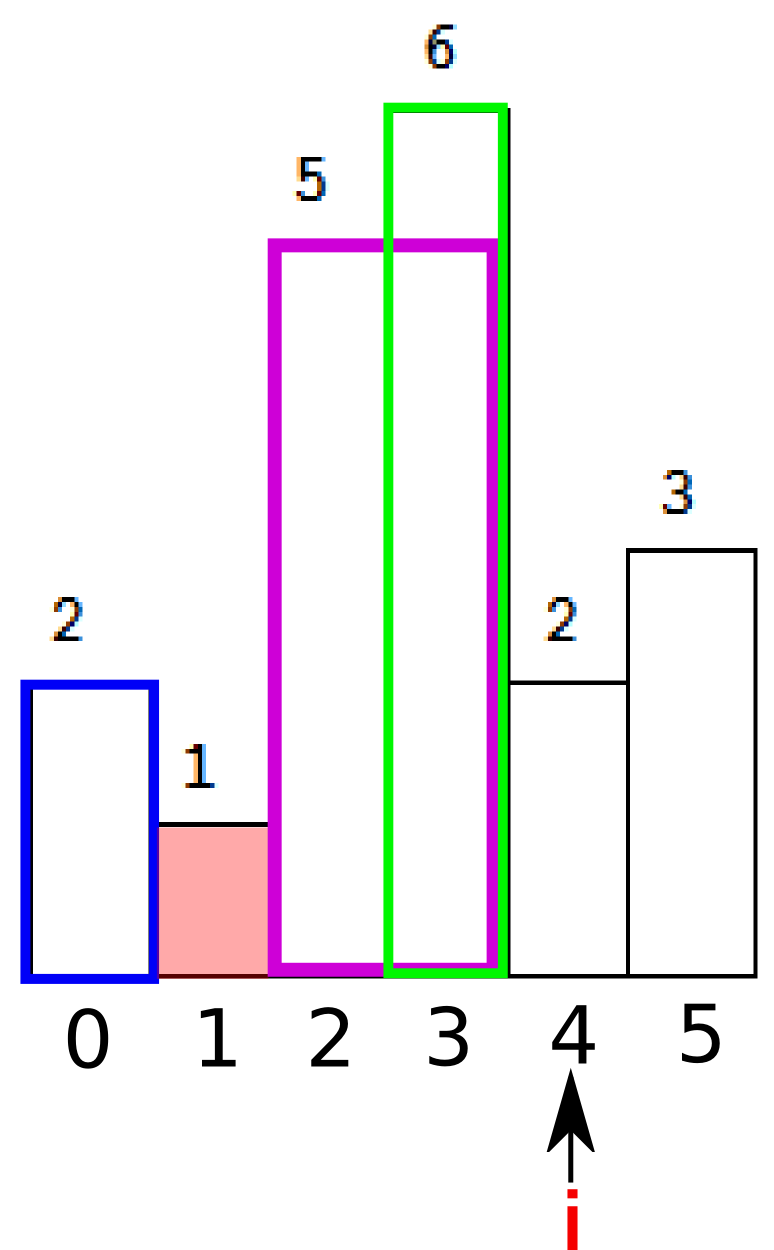
最后，栈顶的（索引指向的）元素大于了当前i指向的元素，循环继续，入栈并推动i前进。直到我们再次遇到下降的元素，也就是我们最后人为添加的dummy元素0.

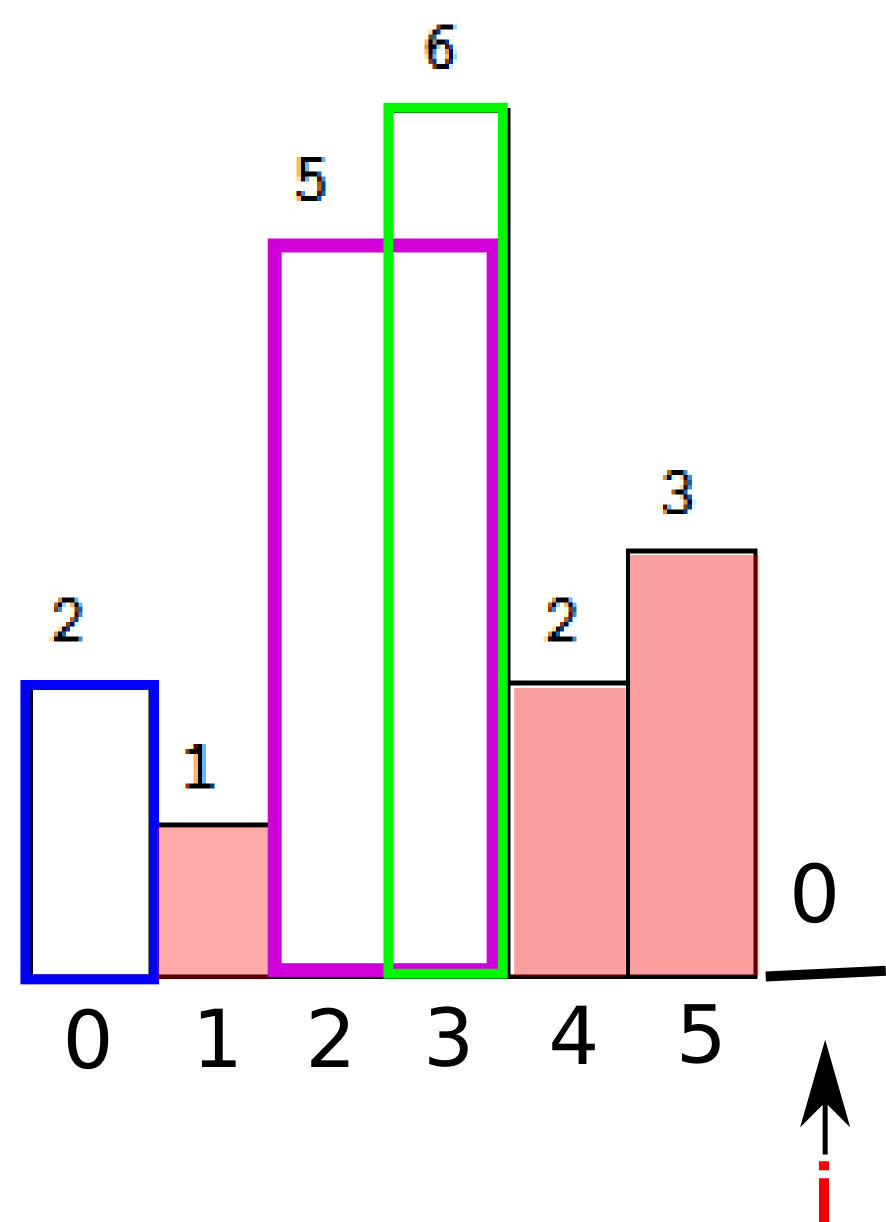
同理，我们计算栈内的面积。由于当前i是最小元素，所以所有的栈内元素都要被弹出并参与面积计算。

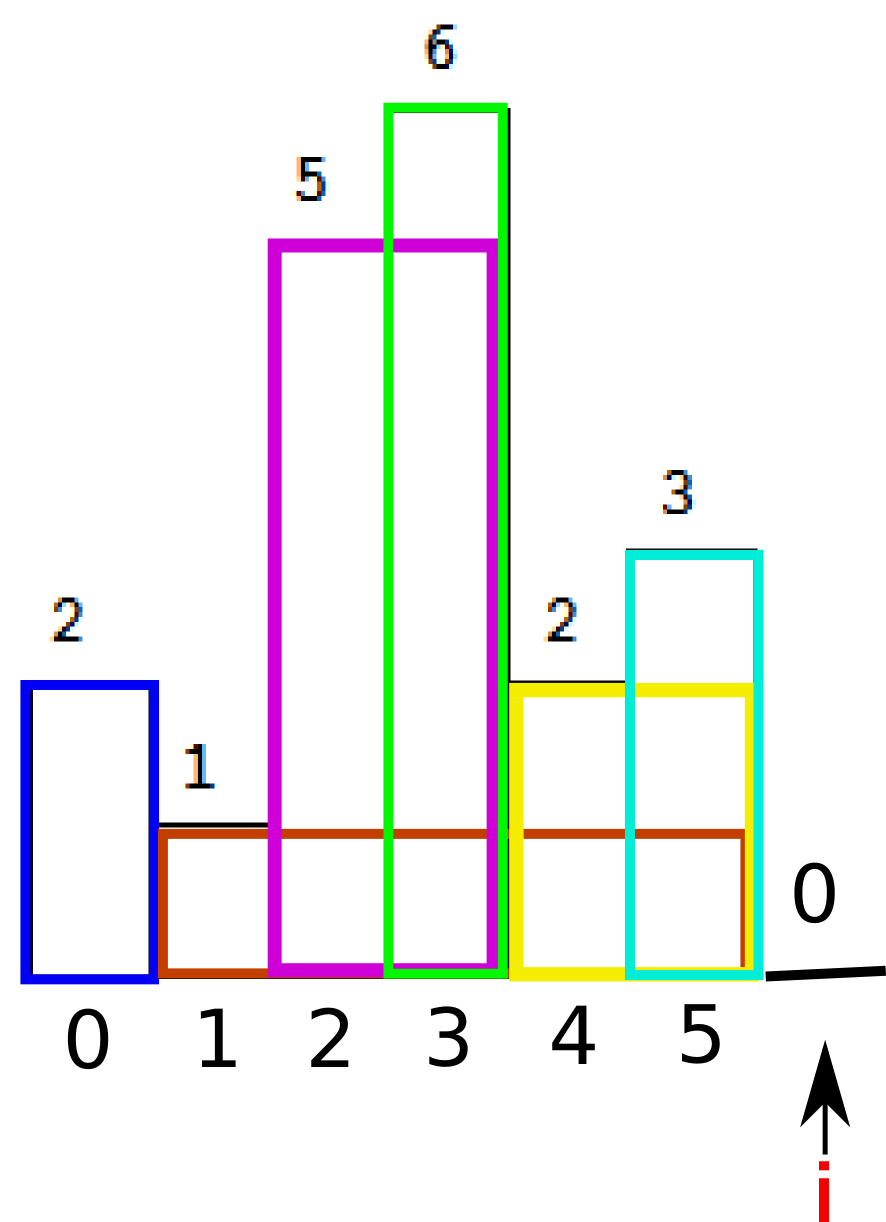
注意我们在计算面积的时候已经更新过了maxArea。

总结下，我们可以看到，stack中总是保持递增的元素的索引，然后当遇到较小的元素后，依次出栈并计算栈中bar能围成的面积，直到栈中元素小于当前元素。

可是为什么这个方法是正确的呢？ 我也没搞清楚。只是觉得不明觉厉了。

-------------------------------------------------更新----------------------------------------------------------------

可以这样理解这个算法，看下图。

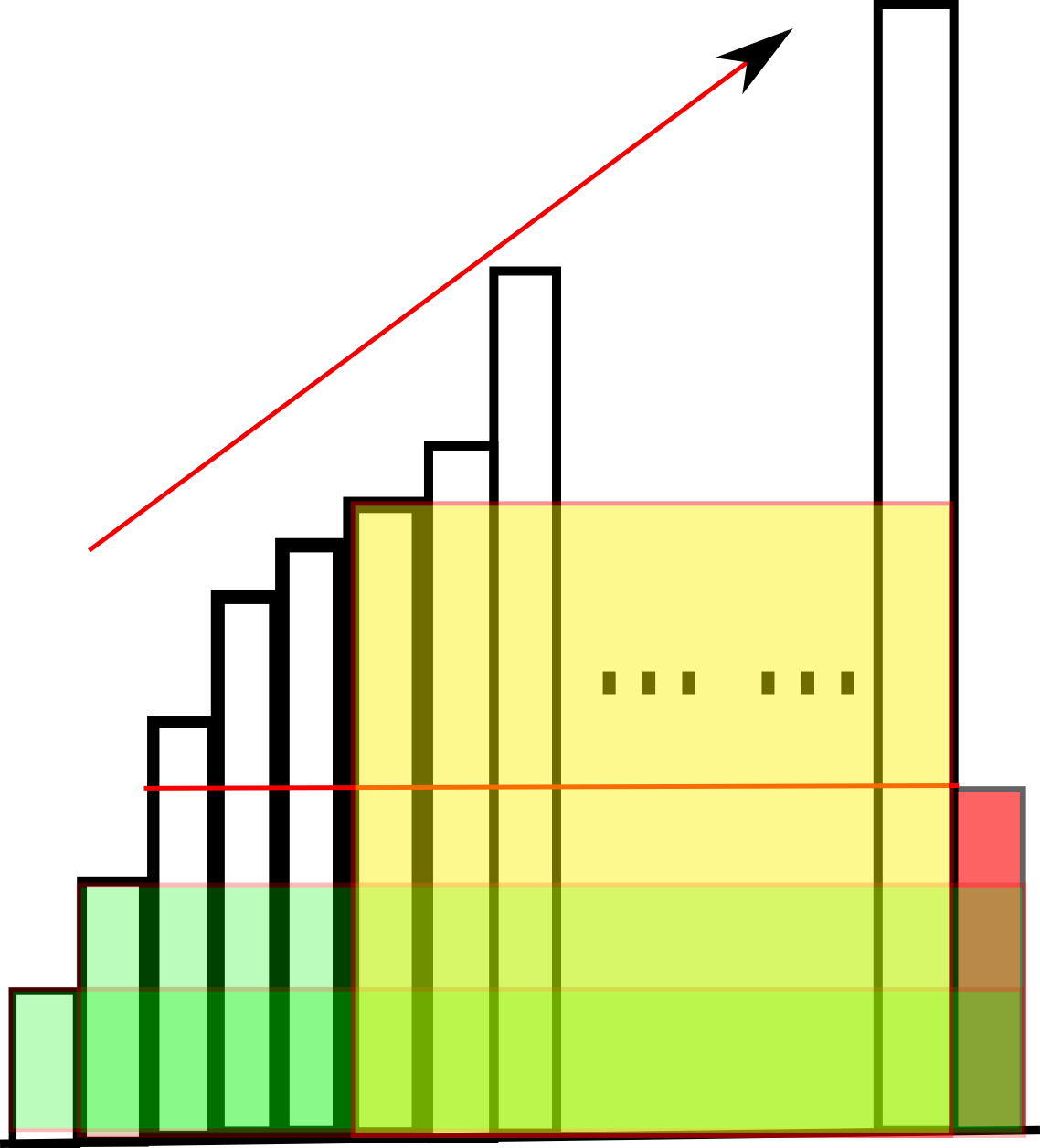
例如我们遇到最后遇到一个递减的bar（红色）。高度位于红线上方的（也就是算法中栈里面大于最右bar的）元素，他们是不可能和最右边的较小高度bar围成一个比大于在弹栈过程中的矩形面积了（黄色面积），因为红色的bar对他们来说是一个短板，和红色bar能围成的最大面积也就是红色的高度乘以这些“上流社会”所跨越的索引范围。但是“上流社会”的高度个个都比红色bar大，他们完全只计算彼此之间围成的面积就远远大于和红色bar围成的任意面积了。所以红色bar是不可能参与“上流社会”的bar的围城的（好悲哀）。

但是屌丝也不用泄气哦。因为虽然长度不占优势，但是团结的力量是无穷的。它还可以参与“比较远的”比它还要屌丝的bar的围城。他们的面积是有可能超过上流社会的面积的，因为距离啊！所以弹栈到比红色bar小就停止了。

另外一个细节需要注意的是，弹栈过程中面积的计算。

h[t] * (stack.isEmpty() ? i : i - stack.peek() - 1)

h[t]是刚刚弹出的栈顶端元素。此时的面积计算是h[t]和前面的“上流社会”能围成的最大面积。这时候要注意哦，栈内索引指向的元素都是比h[t]小的，如果h[t]是目前最小的，那么栈内就是空哦。而在目前栈顶元素和h[t]之间（不包括h[t]和栈顶元素），都是大于他们两者的。如下图所示：

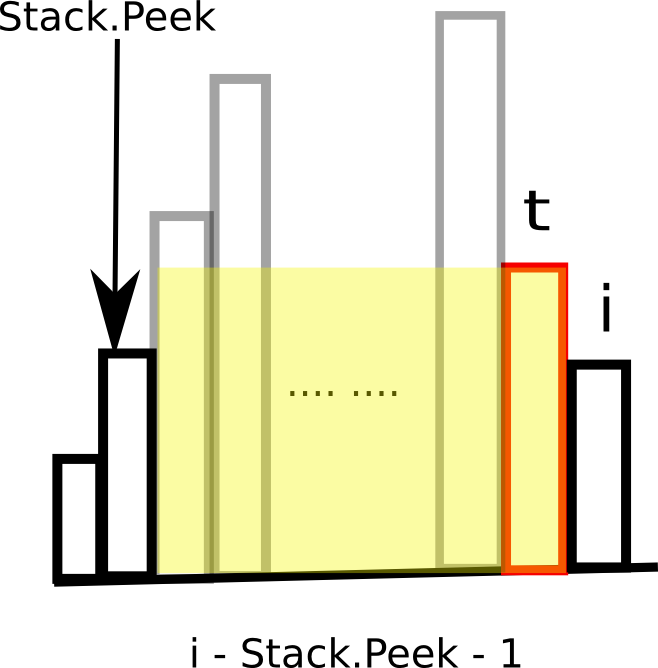
那h[t]无疑就是Stack.Peek和t之间那些上流社会的短板啦，而它们的跨越就是i - Stack.Peek - 1。

所以说，这个弹栈的过程也是维持程序不变量的方法啊：栈内元素一定是要比当前i指向的元素小的。

----------------------------------------------------------------------------------华丽------------------------------------------------------------------------------------------------------------------------

我只想问算法的作者，他们到底是怎么想出来的，在这么短的时间内。是不是有一些类似的研究或者算法给他们以灵感？

太有画面感了有木有！