数据结构-详解优先队列的二叉堆（最大堆）原理、实现和应用-C和Python

一、堆的基础

1.1 优先队列和堆

优先队列（Priority Queue）：特殊的“队列”，取出元素顺序是按元素优先权（关键字）大小，而非元素进入队列的先后顺序。

若采用数组或链表直接实现优先队列，代价高。依靠数组，基于完全二叉树结构实现优先队列，即堆效率更高。一般来说堆代指二叉堆。

 

优先队列的完全二叉树（堆）表示

---

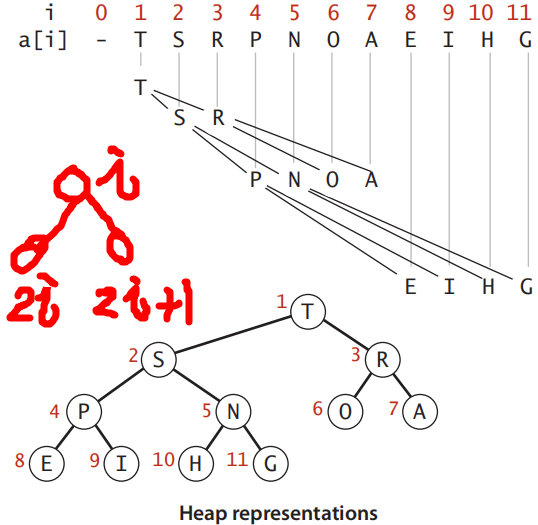
1.2 堆

堆序性： 父节点元素值比孩子节点大（小）

• 最大堆(MaxHeap), 也称“大顶堆”：根节点为最大值；
• 最小堆(MinHeap), 也称“小顶堆” ：根节点为最小值。

通常以最大堆为例。 最小堆实现，直接把最大堆元素值取负。

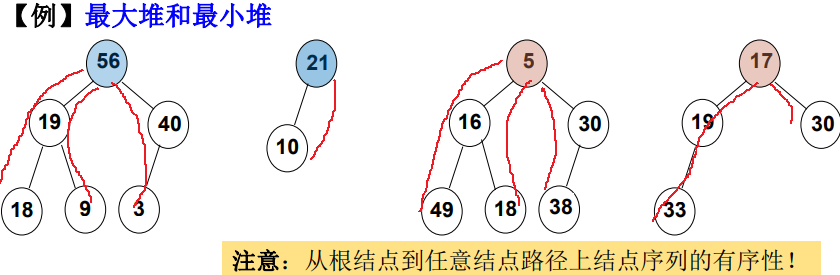
二、最大堆实现

2.1 最大堆操作

最大堆（MaxHeap）数据结构实际为完全二叉树，每个结点的元素值不小于其子结点的元素值。

其主要操作有：

• MaxHeap InitializeHeap( int MaxSize )：初始化一个空的最大堆。
• Boolean IsFull( MaxHeap H )：判断最大堆H是否已满。
• Boolean IsEmpty( MaxHeap H )：判断最大堆H是否为空。
• Insert( MaxHeap H, ElementType X )：将元素X插入最大堆H。
• ElementType DeleteMax( MaxHeap H )：返回H中最大元素(高优先级)。

核心操作为恢复堆序性：在堆中执行了可能违反堆序性的简单修改后，需通过修改堆确保重新满足堆序性。有两种情况：

• 自底向上reheapify（上滤，swim）: 当某个节点的优先级增加时（或在堆的底部添加一个新节点）时，必须向上遍历调整堆以恢复堆序。
• 自顶向下reheapify（下滤, sink）：当节点优先级减少（变小）时（例如，如果用键较小的新节点替换根上的节点），必须向下遍历调整堆以恢复堆顺。

可以先实现这两个基本辅助操作，然后使用它们来实现插入和删除最大值。其操作如下图所示：

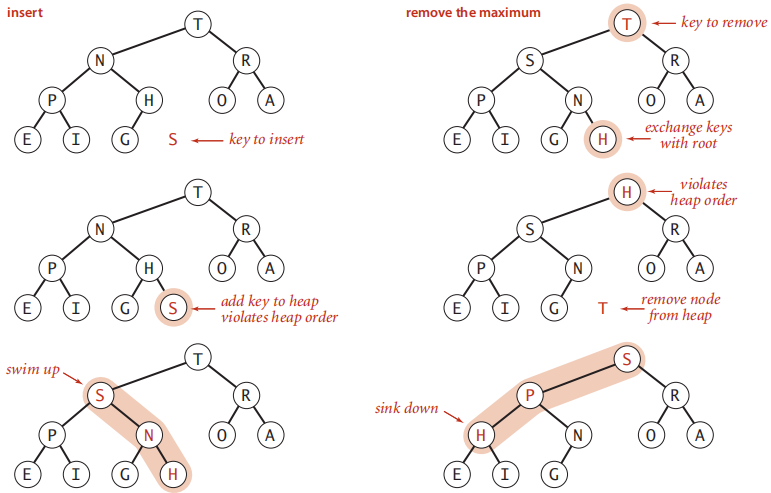
插入-插入元素索引上移，父节点值下移；

删除-孩子节点值上移，末尾元素索引下移（降序插入排序，右边有序，直到找到一个小于它的元素）；

2.2 最大堆C实现

2.2.1 基本操作

声明堆结构

#include <stdlib.h>
#include <stdIo.h>
typedef int ElementType;
typedef struct HNode *Heap; /* 堆的类型定义 */
struct HNode {
    ElementType *Data; /* 存储元素的数组 */
    int Size;          /* 堆中当前元素个数 */
    int Capacity;      /* 堆的最大容量 */
};
typedef Heap MaxHeap; /* 最大堆 */
#define MAXDATA 1000000  /* 该值应根据具体情况定义为大于堆中所有可能元素的值 */
 

初始化堆

MaxHeap InitializeHeap( int MaxSize )
{   /* 创建容量为MaxSize的空的最大堆 */

    MaxHeap H = (MaxHeap)malloc(sizeof(struct HNode));
    /* 多一个元素存放"哨兵" */
    H->Data = (ElementType *)malloc((MaxSize+1)*sizeof(ElementType));  

    H->Size = 0;
    H->Capacity = MaxSize;
    H->Data[0] = MAXDATA;  /* 定义"哨兵"为大于堆中所有可能元素的值*/

    return H;
}

判是否满堆，以及是否为空

bool IsFull( MaxHeap H )
{
    return (H->Size == H->Capacity);
}

bool IsEmpty( MaxHeap H )
{
    return (H->Size == 0);
}

2.2.2 最大堆的插入

将新增结点插入到，从其父结点到根结点的有序序列中 ( 完全二叉树，插入时间复杂度O(logN) ）

一步步往上调整（上滤）

void Insert( MaxHeap H, ElementType X )
{   /* 将元素X插入最大堆H，其中H->Data[0]已经定义为哨兵 */
    int i;
    /* 首先判断，堆是否已满。已满则结束 */
    if ( IsFull(H) ) {
        printf("最大堆已满");
        return;
    }

    /* 若堆未满，i指向堆末尾的下一个位置(空穴，当前size+1)，准备插入X */
    i = ++H->Size;  /* 类似插入排序，  */
    /* 若X 大于 其父节点值，则将父节点值下移至位置i， i位置(空穴）移到父节点位置[i/2] */
    for ( ; H->Data[i/2] < X; i /= 2 )
        H->Data[i] = H->Data[i/2]; /* 上滤X */

    H->Data[i] = X; /* 将X插入 */
    /* 若X是当前堆中最大元素，那么会在堆顶时（比哨兵小）终止上移 */
}

2.2.3 最大堆的删除

删除位置-根结点，返回堆顶（最大值）元素，并调整堆使其保持堆序性（少了一个元素）。

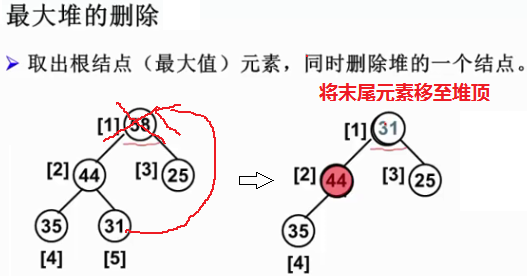
ElementType DeleteMax( MaxHeap H )
{   /* 从最大堆H中取出键值为最大的元素，并删除一个结点 */
    int Parent, Child;   /* 指针 */
    ElementType MaxItem, X;    

    if ( IsEmpty(H) ) {
        printf("最大堆已为空"); /* 若堆已空，则结束（没得删） */
        return ERROR;
    }

    MaxItem = H->Data[1]; /* 取出根结点存放的最大值 */
    /* 用最大堆中最后一个元素X，从根结点开始，向上过滤下层结点 */
    X = H->Data[H->Size--]; /* 相当于删掉末尾元素位置，故当前堆size要减1*/

    /* 迭代地将X和其更大的孩子节点值作比较，并调整位置（从根节点开始，给X找个位置） */
    /* Parent*2 <= H->Size判断是否有左儿子(有无孩子)，若无则超出堆空间，跳出循环，直接把X放Parent */
    for ( Parent = 1; Parent*2 <= H->Size; Parent = Child ) {
        /* 找到当前更大的孩子节点*/
        Child = Parent * 2;  /* 令Child为左儿子，经过外层for循环判断，Child只能 <= Parent */
        /* 若有右儿子((Child < H->Size))，则让让Child指向左右子结点的较大者 */
        if ( (Child != H->Size) && (H->Data[Child] < H->Data[Child+1]) )
            Child++;
        /* 将末尾元素X和Child的值比较，若X >= Child值则结束（有序了）*/
        /* 若X < Child值 (Child更大)，则将Child值放在位置Parent，并将Parent位置移到Child位置 */
        if ( X >= H->Data[Child] )
            break;   /* 找到了合适位置 */
        else  /* Child元素上移，X移动到下一层（Parent = Child），继续和其孩子节点比较 */
            H->Data[Parent] = H->Data[Child];
    }
    H->Data[Parent] = X;

    return MaxItem;
} 

自顶向下，找到更大的孩子节点（孩子不一定是2个，也可能只有1个），并和末尾元素比较

若孩子更小或等于则不动，若孩子更大则将孩子值上移。末尾元素索引下移-下滤

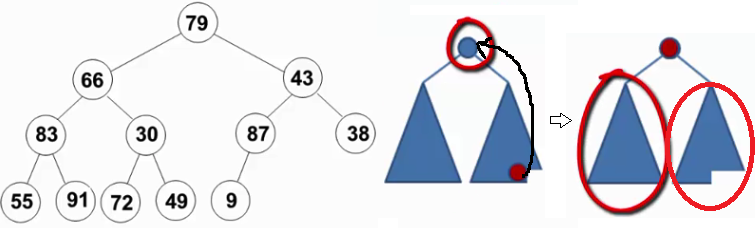
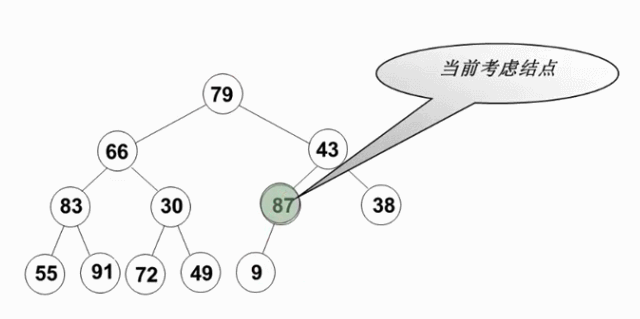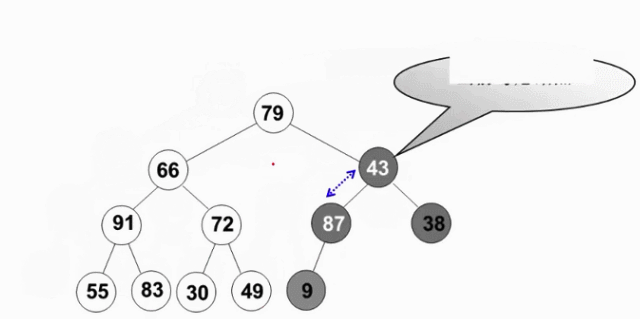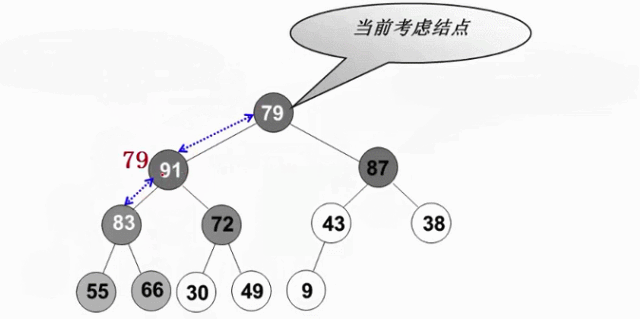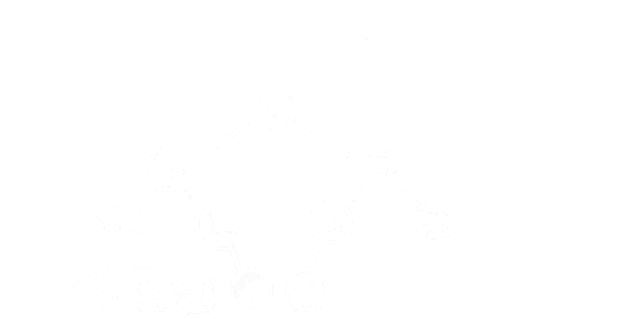
2.2.4 最大堆的建立

将已经存在的N个元素，按最大堆的要求存放在一个一维数组中

方法1：通过插入操作，将N个元素一个个相继插入到一个初始为空的堆中去，其时间代价最大为O(N logN)。

方法2：在线性时间复杂度O(N)下，建立最大堆。

• 将N个元素按输入顺序存入，先满足完全二叉树的结构特性
• 调整各结点位置，以满足最大堆的有序特性

分析：该如何调整堆？

在删除最大值操作中，末尾元素放置于堆顶，此时其左子树和右子树均为堆。其调整思路为，不断地找更大的孩子调上来，自己下沉（下滤操作）。

但是，如上图左子图所示，初始化的堆并不满足堆序性（对79而言，其左右均不是堆，其他节点也是这个情况），似乎不能直接使用删除最大值操作。

 

实际可以逆向思维，找到最小满足该情况的例子：

从倒数第一个有儿子的节点开始（末尾节点的父亲，此节点的左右肯定是堆-叶节点），逆序执行（自底向上，逆层序遍历）下滤操作。这样当目标节点的左子树和右子树都为堆时，就可以自然地复用删除最大值操作

void PercolateDown( MaxHeap H, int p )
{   /* 下滤：将H中以H->Data[p]为根的子堆调整为最大堆 */
    int Parent, Child;
    ElementType X = H->Data[p]; /* 取出根结点存放的值 */
    for ( Parent=p; Parent*2<=H->Size; Parent=Child ) {
        Child = Parent * 2;
        if ( (Child!=H->Size) && (H->Data[Child]<H->Data[Child+1]) )
            Child++;  /* Child指向左右子结点的较大者 */
        if ( X >= H->Data[Child] )  break; /* 找到了合适位置 */
        else  /* 下滤X */
            H->Data[Parent] = H->Data[Child];
    }
    H->Data[Parent] = X;
}

void BuildHeap( MaxHeap H )
{   /* 调整H->Data[]中的元素，使满足最大堆的有序性  */
    /* 这里假设所有H->Size个元素已经存在H->Data[]中 */

    int i;

    /* 从最后一个结点的父节点开始，到根结点1 */
    for ( i = H->Size/2; i > 0; i-- )
        PercolateDown( H, i );
}

分析

倒数第2层最多交换1次， 其余节点的交换次数此时按其深度线性递增（节点数按2的对数下降）

 

基于下滤操作的删除最大值实现：

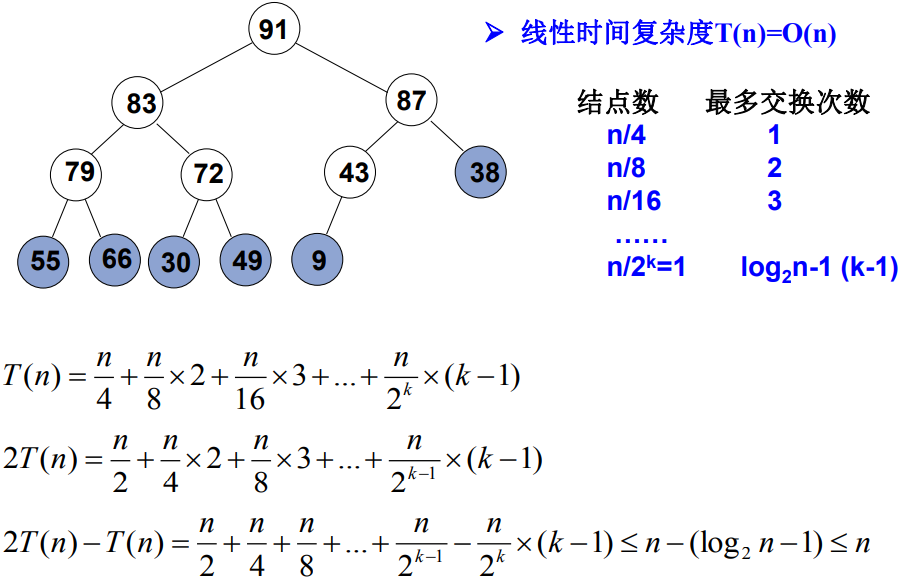
ElementType DeleteMax( MaxHeap H )
{   /* 从最大堆H中取出键值为最大的元素，并删除一个结点 */

    ElementType MaxItem = H->Data[1]; /* 取出根结点存放的最大值 */

    H->Data[1] = H->Data[H->Size--]   /* 取出根结点存放的最大值 */

    PercolateDown(H, 1);  /* 从根结点开始，向上过滤下层结点（末尾节点下滤） */
    return MaxItem;
} 

可知，删除最大值中的调整操作是BuildHeap的特例。此外，还有删除堆中某个元素、增大某个元素的优先级和减小某个元素的优先级的操作。高效执行此操作的前提 ，是用哈希表简历key到index的映射。

2.3 最大堆Python实现

逻辑参照上述C语言版

class Heap:
    def __init__(self, n):
        self.capacity = n
        self.size = 0
        self.arr = [None] * (self.capacity+1)
        self.arr[0] = 2e24

    def insert(self, num):
        if self.size == self.capacity:
            print("Out of size")
        else:
            self.size += 1
            child = self.size  # 空穴位置
            # 上滤, 当左儿子在堆范围内
            while num > self.arr[child // 2]:
                parent = child // 2
                self.arr[child] = self.arr[parent]
                child = parent

            self.arr[child] = num

    def pop(self):
        if self.size == 0:
            print("Empty")
        else:
            max_item = self.arr[1] # 取堆顶
            x = self.arr[self.size] # 取堆末尾元素
            self.size -= 1

            parent = 1
            # 下滤, 当左儿子在堆范围内
            while parent * 2  <= self.size:
                child = parent * 2
                if child != self.size and self.arr[child+1] > self.arr[child]:
                    child += 1
                if self.arr[child] > x:
                    self.arr[parent] = self.arr[child] # 孩子节点值上移
                    parent = child
                else:
                    break
            self.arr[parent] = x
            return max_item

调用python包

import queue
, random

class Heap():
    def __init__(self, k):
        if k > 0:
            self.q = queue.PriorityQueue(k)

    def queue(self):
        return self.q.queue

    def enque(self, key):
        # 当前堆大小小于其容量
        if self.q._qsize() < self.q.maxsize:
            self.q.put(key)
        else:
            self.q.get() # 删除堆顶
            self.q.put(key)

    def deque(self):
        if not self.q.empty():
            return self.q.get()
        else:
            print("Empty heap")

h1 = Heap(10)
for i in range(15):
    h1.enque(i)

print(h1.queue())  # 最小堆，k  可得到堆排序得到最大的k个 

l1 = [ random.randint(1, 100) for i in range(20)]
print(l1)

for i in l1:
    h1.enque(i)

print(h1.queue())
print("\nPriority Queue:")
print([h1.deque() for i in range(h1.q._qsize())])

三、堆的应用

经典的应用有选择问题、堆排序和Huffman编码等等。

3.1. 选择问题

问题描述：输入N个数，找到第k个最大的数。如果K=N/2，就是找中位数， 这是选择问题的最困难的情况。

暴力法：直接排序，并返回排序数组的倒数第K个数，O(NlogN)，

使用堆：

算法A: 大优先队列

• 将N个元素读入数组，并构建最大堆O(N)
• 然后执行K次删除最大元素O(KlogN)

最后一次删除的元素就是第K个最大值，总时间复杂度：O(N + KlogN)。

• 如果k小时，运行时间取决于建堆O(N)。
• 如果k大时，运行时间取决于删除O(KlogN)。例如K=N，即O(NlogN)，直接堆排序
• 如果K=N/2，平均时间复杂度(NlogN)

---

算法B: 小优先队列（流式处理）

• 将K个元素读入数组，并构建最小堆O(K)
• 依次删除最小堆的最小元素，再将元素插入最小堆（把待插入元素放在堆顶，然后下滤）O((N-K)logK)

因此，O(K + (N-K)logK) = O(K(1-logK) + NlogK) = O(NlogK)

3.2 堆排序

• 将N个元素读入数组，并构建最大堆O(N) Heap的原理和实现
• 然后，执行N-1次删除最大元素O(NlogN)，返回的元素构成的数组有序

每次删除元素可以放在当前堆尾。慢于希尔排序。

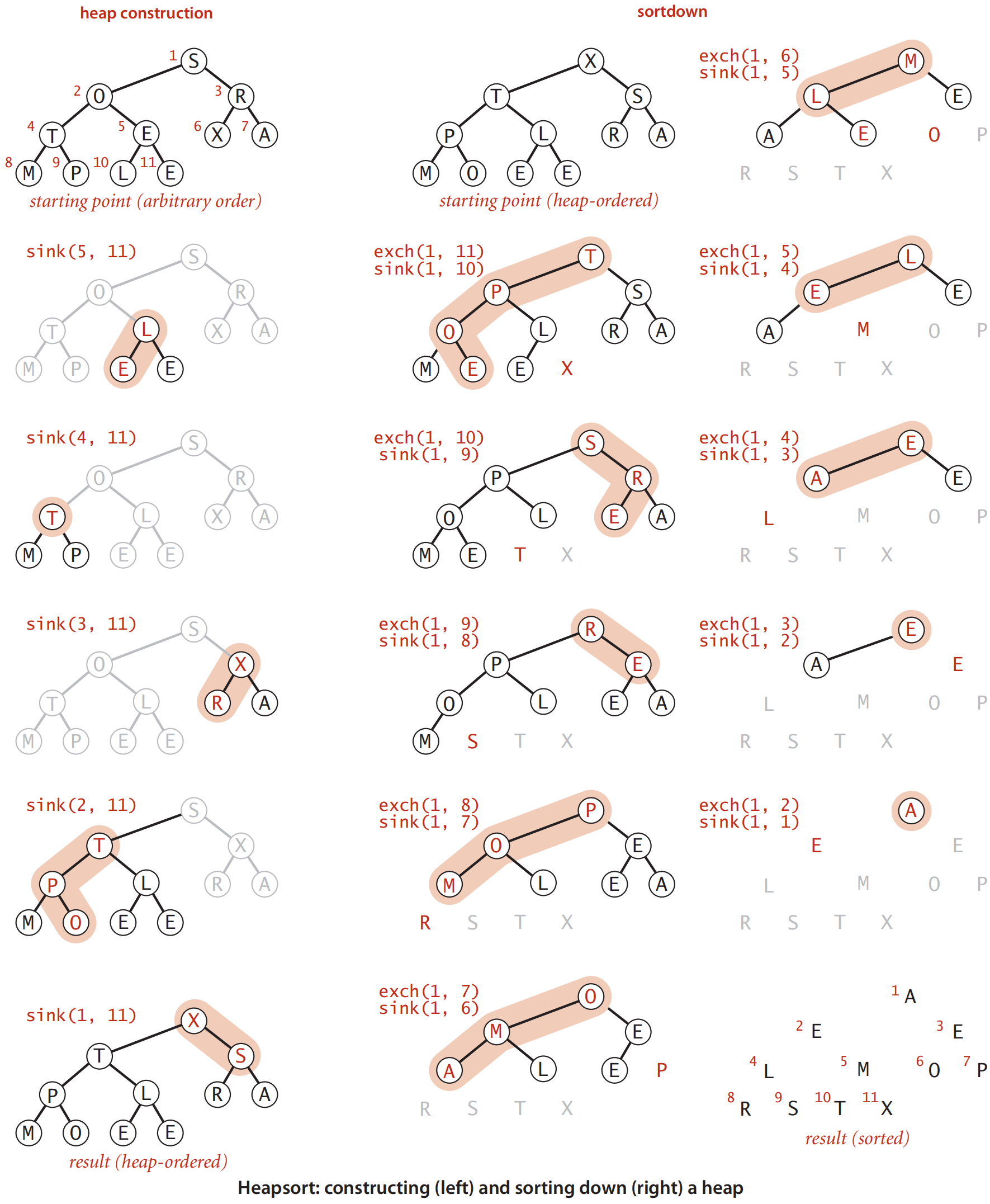
1. 实际实现时，先自底向上调用N/2 + 1次下滤操作PercolateDown，线性建堆。
2. 然后，每次把堆顶元素和堆末尾元素交换，将堆size减1，并从根节点执行下滤操作PercolateDown。共计N-1次（最后一个元素已经在堆顶，不需要操作）

堆排序不完全同于二叉堆的删除，其数组元素初始位置在0，所以下滤开始位置为0而不是1，下滤范围从N-1到1（实际堆的大小）。

Python调包版

def sortArray(nums: List[int]) -> List[int]:
    import heapq
    heapq.heapify(nums)
    return [heapq.heappop(nums) for i in range(len(nums))] 

Python实现

class Solution:
    def sortArray(self, nums: List[int]) -> List[int]:
        def heapify(nums, parent, arr_size):
            # parent为开始下滤节点索引，p为当前堆大小(决定调整边界)
            x = nums[parent]
            # 下滤, 当左儿子在堆范围内
            while parent * 2 + 1 < arr_size:
                child = parent * 2 + 1
                if child != arr_size-1 and nums[child+1] > nums[child]:
                    child += 1
                if nums[child] > x:
                    nums[parent] = nums[child]
                    parent = child
                else:
                    break
            nums[parent] = x

        # 构建堆
        n = len(nums)
        for i in range(n//2, -1, -1):
            heapify(nums, i, n)  # 建堆时堆大小固定为其容量
        # 迭代删除堆顶元素
        for i in range(n-1, 0, -1):
            # 将堆顶元素取出（直接在末尾存储），把末尾元素放堆顶
            nums[i], nums[0] = nums[0], nums[i]
            heapify(nums, 0, i) # 然后下滤
        return nums                

C实现

void PercolateDown( ElementType A[], int p, int N )
{
   /* 将N个元素的数组中以A[p]为根的子堆调整为最大堆 */
    int Parent, Child;
    ElementType X = A[p]; /* 取出根结点存放的值 */
    for ( Parent=p; (Parent*2+1) < N; Parent=Child ) {
        Child = Parent * 2 + 1;
        if ( (Child != N-1) && (A[Child] < A[Child+1]) )
            Child++;  /* Child指向左右子结点的较大者 */
        if ( X >= A[Child] ) break; /* 找到了合适位置 */
        else  /* 下滤X */
            A[Parent] = A[Child];
    }
    A[Parent] = X;
}

void HeapSort( ElementType A[], int N )
{
     int i;
     /* 建立最大堆 */
     for ( i = N/2-1; i >= 0; i-- )
         PercolateDown( A, i, N );

     for ( i=N-1; i>0; i-- ) {
         /* 删除最大堆顶 */
         Swap( &A[0], &A[i] );
         PercolateDown( A, 0, i );
     }
}

 

参考资料：算法第四版，浙江大学-数据结构慕课