poj 1037 三维dp

A decorative fence

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 7221		Accepted: 2723

Description

Richard just finished building his new house. Now the only thing the house misses is a cute little wooden fence. He had no idea how to make a wooden fence, so he decided to order one. Somehow he got his hands on the ACME Fence Catalogue 2002, the ultimate resource on cute little wooden fences. After reading its preface he already knew, what makes a little wooden fence cute. 
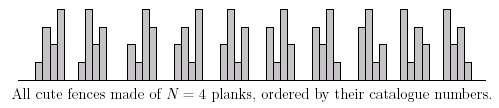
A wooden fence consists of N wooden planks, placed vertically in a row next to each other. A fence looks cute if and only if the following conditions are met: 
�The planks have different lengths, namely 1, 2, . . . , N plank length units. 
�Each plank with two neighbors is either larger than each of its neighbors or smaller than each of them. (Note that this makes the top of the fence alternately rise and fall.) 
It follows, that we may uniquely describe each cute fence with N planks as a permutation a1, . . . , aN of the numbers 1, . . . ,N such that (any i; 1 < i < N) (ai − ai−1)*(ai − ai+1) > 0 and vice versa, each such permutation describes a cute fence. 
It is obvious, that there are many dierent cute wooden fences made of N planks. To bring some order into their catalogue, the sales manager of ACME decided to order them in the following way: Fence A (represented by the permutation a1, . . . , aN) is in the catalogue before fence B (represented by b1, . . . , bN) if and only if there exists such i, that (any j < i) aj = bj and (ai < bi). (Also to decide, which of the two fences is earlier in the catalogue, take their corresponding permutations, find the first place on which they differ and compare the values on this place.) All the cute fences with N planks are numbered (starting from 1) in the order they appear in the catalogue. This number is called their catalogue number. 

After carefully examining all the cute little wooden fences, Richard decided to order some of them. For each of them he noted the number of its planks and its catalogue number. Later, as he met his friends, he wanted to show them the fences he ordered, but he lost the catalogue somewhere. The only thing he has got are his notes. Please help him find out, how will his fences look like.

Input

The first line of the input file contains the number K (1 <= K <= 100) of input data sets. K lines follow, each of them describes one input data set. 
Each of the following K lines contains two integers N and C (1 <= N <= 20), separated by a space. N is the number of planks in the fence, C is the catalogue number of the fence. 
You may assume, that the total number of cute little wooden fences with 20 planks fits into a 64-bit signed integer variable (long long in C/C++, int64 in FreePascal). You may also assume that the input is correct, in particular that C is at least 1 and it doesn抰 exceed the number of cute fences with N planks.

Output

For each input data set output one line, describing the C-th fence with N planks in the catalogue. More precisely, if the fence is described by the permutation a1, . . . , aN, then the corresponding line of the output file should contain the numbers ai (in the correct order), separated by single spaces.

Sample Input

2
2 1
3 3

Sample Output

1 2
2 3 1

Source

CEOI 2002

 

题意：除了两端的木棒外，每一跟木棒，要么比它左右的两根都长，要么比它左右的两根都短

符合上述条件的栅栏建法有很多种，对于满足条件的所有栅栏, 按照字典序(从左到右, 从低到高) 排序。

 给定一个栅栏的排序号，请输出该栅栏, 即每一个木棒的长度.

 

题解：参考自pku_gw 代码 涨思路

C[i][k][DOWN] 是S(i)中以第k短的木棒打头的DOWN方案数,（第一根比第二根长成为down方案）

C[i][k][UP] 是S(i)中以第k短的木棒打头的UP方案数,第k短指i根中第k短  具体看代码

 

 /******************************
 code by drizzle
 blog: www.cnblogs.com/hsd-/
 ^ ^    ^ ^
  O      O
 ******************************/
 //#include<bits/stdc++.h>
 #include<iostream>
 #include<cstring>
 #include<cmath>
 #include<cstdio>
 #define ll long long
 #define mod 1000000007
 #define PI acos(-1.0)
 using namespace std;
 int UP=;
 int DOWN=;
 ll c[][][];
 void init(int n)
 {
     memset(c,,sizeof(c));
     c[][][UP]=c[][][DOWN]=;//初始为1种
     for(int i=; i<=n; i++)
     {
         for(int k=; k<=i; k++)
         {
             for(int m=k; m<i; m++)
                 c[i][k][UP]+=c[i-][m][DOWN];//前i-1的down方案m>=k
             for(int l=; l<=k-; l++)
                 c[i][k][DOWN]+=c[i-][l][UP];//前i-1的up方案 l<k
         }
     }
 }
 void fun(int n,ll cc)//排序计数处理 ，一位一位的判断 不断靠近cc
 {
     ll skipped=;//已经跳过的方案数
     int seq[];
     int used[];
     memset(used,,sizeof(used));
     for(int i=; i<=n; i++)
     {
         ll oldval=skipped;
         int k;
         int no=;
         for(k=; k<=n; k++)
         {
             oldval=skipped;
             if(!used[k])
             {
                 no++;//k是剩下的木棒里第no短的
                 if(i==)//首位
                     skipped+=c[n][no][UP]+c[n][no][DOWN];
                 else
                 {  //剩下n-i+1条木棒 现在放置第no短的木棒k 判断k与已经确定的seq的前一条木棒的关系
                     if(k>seq[i-]&&(i<=||seq[i-]>seq[i-]))
                         skipped+=c[n-i+][no][DOWN];//判断合理的放置
                     else if(k<seq[i-]&&(i<=||seq[i-]<seq[i-]))
                         skipped+=c[n-i+][no][UP];
                 }
                 if(skipped>=cc)//当跳过的方案数大于询问的数目跳出
                     break;
             }
         }
         used[k]=;
         seq[i]=k;
         skipped=oldval;
     }
     for(int i=; i<=n; i++)
         if(i<n) printf("%d ",seq[i]);
         else    printf("%d\n",seq[i]);

 }
 int main()
 {
     int T,s;
     ll c;
     init();
     scanf("%d",&T);
     while(T--)
     {
         scanf("%d %I64d",&s,&c);
         fun(s,c);
     }
     return ;
 }