R_Studio(时序)Apriori算法寻找频繁项集的方法

　　应用ARIMA(1，1，0)对2015年1月1日到2015年2月6日某餐厅的销售数量做为期5天的预测

　　

setwd('D:\\dat')

#install.packages("forecast")
#install.packages("plyr")
#install.packages("fUnitRoots")
#install.packages("tibble")

library(forecast)
library(fUnitRoots)
Data=read.csv("arima_data.csv",header=T)[,2]
sales=ts(Data)
plot.ts(sales,xlab="时间", ylab="销量 / 元")

#单位根检验
unitrootTest(sales)
#自相关图
acf(sales)
#一阶差分
difsales=diff(sales)
plot.ts(difsales,xlab="时间", ylab="销量残差 / 元")
#自相关图
acf(difsales)
#单位根检验
unitrootTest(difsales)

#白噪声检验
Box.test(difsales, type="Ljung-Box")
#偏自相关图
pacf(difsales)
#ARIMA(1,1,0)模型
arima=arima(sales, order=c(1,1,0))
arima
forecast=forecast(arima, h=5, level=c(99.5))
forecast

Gary.R

实现过程

　　数据预处理

setwd('D:\\dat')

#install.packages("forecast")
#install.packages("plyr")
#install.packages("fUnitRoots")
#install.packages("tibble")

library(forecast)
library(fUnitRoots)
Data=read.csv("arima_data.csv",header=T)[,2]
sales=ts(Data)
plot.ts(sales,xlab="时间", ylab="销量 / 元")

相关检验

　　单位根检验　　百度百科：传送门

　　单位根检验是指检验序列中是否存在单位根，因为存在单位根就是非平稳时间序列了。单位根就是指单位根过程，可以证明，序列中存在单位根过程就不平稳，会使回归分析中存在伪回归。

> #单位根检验
> unitrootTest(sales)

Title:
 Augmented Dickey-Fuller Test

Test Results:
  PARAMETER:
    Lag Order: 1
  STATISTIC:
    DF: 1.6708
  P VALUE:
    t: 0.9748
    n: 0.9745 

Description:
 Thu Nov 29 21:45:16 2018 by user: ASUS

　　自相关　　百度百科：传送门

　　自相关是指信号在1个时刻的瞬时值与另1个时刻的瞬时值之间的依赖关系，是对1个随机信号的时域描述。

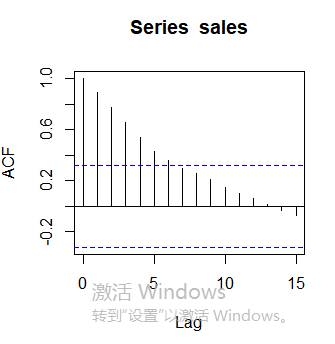
#自相关图
acf(sales)

　　

#自相关图
acf(difsales)

　　

　　一阶差分　　百度百科：传送门

　　一阶差分就是离散函数中连续相邻两项之差。当自变量从x变到x+1时，函数y=y(x)的改变量∆yx=y(x+1)-y(x)，(x=0，1，2，......)称为函数 y(x)在点x的一阶差分，记为∆yx=yx+1-yx，(x=0，1，2，......)

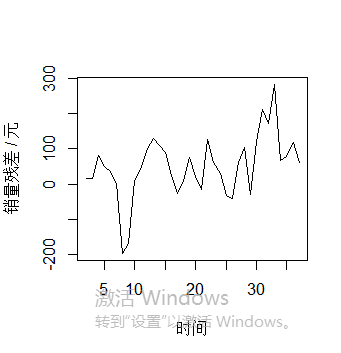
#一阶差分
difsales=diff(sales)
plot.ts(difsales,xlab="时间", ylab="销量残差 / 元")

　　

　　单位根检验　　百度百科：传送门

　　单位根检验是指检验序列中是否存在单位根，因为存在单位根就是非平稳时间序列了。单位根就是指单位根过程，可以证明，序列中存在单位根过程就不平稳，会使回归分析中存在伪回归。

> unitrootTest(difsales)

Title:
 Augmented Dickey-Fuller Test

Test Results:
  PARAMETER:
    Lag Order: 1
  STATISTIC:
    DF: -2.4226
  P VALUE:
    t: 0.01689
    n: 0.2727 

Description:
 Thu Nov 29 21:50:32 2018 by user: ASUS

　　白噪声检验　　百度百科：传送门

　　白噪声序列，是指白噪声过程的样本实称，简称白噪声。随机变量X（t）（t=1，2，3……），如果是由一个不相关的随机变量的序列构成的，即对于所有S不等于T，随机变量Xt和Xs的协方差为零，则称其为纯随机过程。对于一个纯随机过程来说，若其期望为0，方差为常数，则称之为白噪声过程。

> #白噪声检验
> Box.test(difsales, type="Ljung-Box")

    Box-Ljung test

data:  difsales
X-squared = 11.304, df = 1, p-value = 0.0007734

　　ARIMA(1,1,0)模型　　百度百科：传送门

　　ARIMA模型全称为自回归积分滑动平均模型，所谓ARIMA模型，是指将非平稳时间序列转化为平稳时间序列，然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。ARIMA模型根据原序列是否平稳以及回归中所含部分的不同，包括移动平均过程（MA）、自回归过程（AR）、自回归移动平均过程（ARMA）以及ARIMA过程。

> arima=arima(sales, order=c(1,1,0))
> arima

Call:
arima(x = sales, order = c(1, 1, 0))

Coefficients:
         ar1
      0.6353
s.e.  0.1236

sigma^2 estimated as 5969:  log likelihood = -207.84,  aic = 419.68
> forecast=forecast(arima, h=5, level=c(99.5))
> forecast
   Point Forecast  Lo 99.5  Hi 99.5
38       4856.386 4639.508 5073.263
39       4881.405 4465.699 5297.112
40       4897.299 4290.401 5504.198
41       4907.396 4122.477 5692.315
42       4913.810 3964.980 5862.639