神经网络优化篇：详解dropout 正则化（Dropout Regularization）

dropout 正则化

除了\(L2\)正则化，还有一个非常实用的正则化方法——“Dropout（随机失活）”。

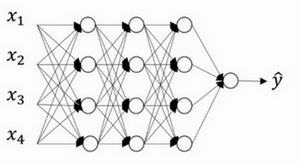
假设在训练上图这样的神经网络，它存在过拟合，这就是dropout所要处理的，复制这个神经网络，dropout会遍历网络的每一层，并设置消除神经网络中节点的概率。假设网络中的每一层，每个节点都以抛硬币的方式设置概率，每个节点得以保留和消除的概率都是0.5，设置完节点概率，会消除一些节点，然后删除掉从该节点进出的连线，最后得到一个节点更少，规模更小的网络，然后用backprop方法进行训练。

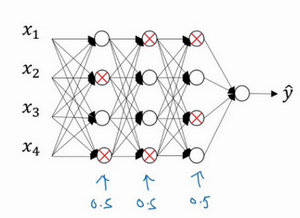
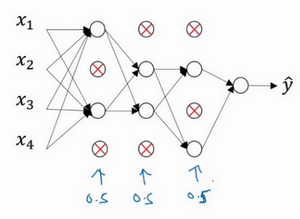
这是网络节点精简后的一个样本，对于其它样本，照旧以抛硬币的方式设置概率，保留一类节点集合，删除其它类型的节点集合。对于每个训练样本，都将采用一个精简后神经网络来训练它，这种方法似乎有点怪，单纯遍历节点，编码也是随机的，可它真的有效。不过可想而知，针对每个训练样本训练规模小得多的网络，最后可能会认识到为什么要正则化网络，因为在训练规模小得多的网络。

如何实施dropout呢？方法有几种，接下来要讲的是最常用的方法，即inverted dropout（反向随机失活），出于完整性考虑，用一个三层（\(l=3\)）网络来举例说明。编码中会有很多涉及到3的地方。只举例说明如何在某一层中实施dropout。

首先要定义向量\(d\)，\(d^{[3]}\)表示网络第三层的dropout向量：

d3 = np.random.rand(a3.shape[0],a3.shape[1])

然后看它是否小于某数，称之为keep-prob，keep-prob是一个具体数字，上个示例中它是0.5，而本例中它是0.8，它表示保留某个隐藏单元的概率，此处keep-prob等于0.8，它意味着消除任意一个隐藏单元的概率是0.2，它的作用就是生成随机矩阵，如果对\(a^{[3]}\)进行因子分解，效果也是一样的。\(d^{[3]}\)是一个矩阵，每个样本和每个隐藏单元，其中\(d^{[3]}\)中的对应值为1的概率都是0.8，对应为0的概率是0.2，随机数字小于0.8。它等于1的概率是0.8，等于0的概率是0.2。

接下来要做的就是从第三层中获取激活函数，这里叫它\(a^{[3]}\)，\(a^{[3]}\)含有要计算的激活函数，\(a^{[3]}\)等于上面的\(a^{[3]}\)乘以\(d^{[3]}\)，a3 =np.multiply(a3,d3)，这里是元素相乘，也可写为\(a3*=d3\)，它的作用就是让\(d^{[3]}\)中所有等于0的元素（输出），而各个元素等于0的概率只有20%，乘法运算最终把\(d^{\left\lbrack3 \right]}\)中相应元素输出，即让\(d^{[3]}\)中0元素与\(a^{[3]}\)中相对元素归零。

如果用python实现该算法的话，\(d^{[3]}\)则是一个布尔型数组，值为true和false，而不是1和0，乘法运算依然有效，python会把true和false翻译为1和0，大家可以用python尝试一下。

最后，向外扩展\(a^{[3]}\)，用它除以0.8，或者除以keep-prob参数。

下面解释一下为什么要这么做，为方便起见，假设第三隐藏层上有50个单元或50个神经元，在一维上\(a^{[3]}\)是50，通过因子分解将它拆分成\(50×m\)维的，保留和删除它们的概率分别为80%和20%，这意味着最后被删除或归零的单元平均有10（50×20%=10）个，现在看下\(z^{\lbrack4]}\)，\(z^{[4]} = w^{[4]} a^{[3]} + b^{[4]}\)，的预期是，\(a^{[3]}\)减少20%，也就是说\(a^{[3]}\)中有20%的元素被归零，为了不影响\(z^{\lbrack4]}\)的期望值，需要用\(w^{[4]} a^{[3]}/0.8\)，它将会修正或弥补所需的那20%，\(a^{[3]}\)的期望值不会变，划线部分就是所谓的dropout方法。

它的功能是，不论keep-prop的值是多少0.8，0.9甚至是1，如果keep-prop设置为1，那么就不存在dropout，因为它会保留所有节点。反向随机失活（inverted dropout）方法通过除以keep-prob，确保\(a^{[3]}\)的期望值不变。

事实证明，在测试阶段，当评估一个神经网络时，也就是用绿线框标注的反向随机失活方法，使测试阶段变得更容易，因为它的数据扩展问题变少。

据了解，目前实施dropout最常用的方法就是Inverted dropout，建议大家动手实践一下。Dropout早期的迭代版本都没有除以keep-prob，所以在测试阶段，平均值会变得越来越复杂，不过那些版本已经不再使用了。

现在使用的是\(d\)向量，会发现，不同的训练样本，清除不同的隐藏单元也不同。实际上，如果通过相同训练集多次传递数据，每次训练数据的梯度不同，则随机对不同隐藏单元归零，有时却并非如此。比如，需要将相同隐藏单元归零，第一次迭代梯度下降时，把一些隐藏单元归零，第二次迭代梯度下降时，也就是第二次遍历训练集时，对不同类型的隐藏层单元归零。向量\(d\)或\(d^{[3]}\)用来决定第三层中哪些单元归零，无论用foreprop还是backprop，这里只介绍了foreprob。

如何在测试阶段训练算法，在测试阶段，已经给出了\(x\)，或是想预测的变量，用的是标准计数法。用\(a^{\lbrack0]}\)，第0层的激活函数标注为测试样本\(x\)，在测试阶段不使用dropout函数，尤其是像下列情况：

\(z^{[1]} = w^{[1]} a^{[0]} + b^{[1]}\)

\(a^{[1]} = g^{[1]}(z^{[1]})\)

\(z^{[2]} = \ w^{[2]} a^{[1]} + b^{[2]}\)

\(a^{[2]} = \ldots\)

以此类推直到最后一层，预测值为\(\hat{y}\)。

显然在测试阶段，并未使用dropout，自然也就不用抛硬币来决定失活概率，以及要消除哪些隐藏单元了，因为在测试阶段进行预测时，不期望输出结果是随机的，如果测试阶段应用dropout函数，预测会受到干扰。理论上，只需要多次运行预测处理过程，每一次，不同的隐藏单元会被随机归零，预测处理遍历它们，但计算效率低，得出的结果也几乎相同，与这个不同程序产生的结果极为相似。

Inverted dropout函数在除以keep-prob时可以记住上一步的操作，目的是确保即使在测试阶段不执行dropout来调整数值范围，激活函数的预期结果也不会发生变化，所以没必要在测试阶段额外添加尺度参数，这与训练阶段不同。

\(l=keep-prob\)

这就是dropout。