数据降维-NMF非负矩阵分解

1.什么是非负矩阵分解？

NMF的基本思想可以简单描述为：对于任意给定的一个非负矩阵V，NMF算法能够寻找到一个非负矩阵W和一个非负矩阵H，使得满足 ，从而将一个非负的矩阵分解为左右两个非负矩阵的乘积。如下图所示，其中要求分解后的矩阵H和W都必须是非负矩阵。

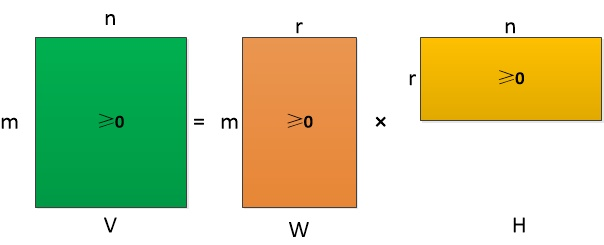
分解前后可理解为：原始矩阵的列向量是对左矩阵中所有列向量的加权和，而权重系数就是右矩阵对应列向量的元素，故称为基矩阵，为系数矩阵。一般情况下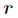的选择要比小，即满足，这时用系数矩阵代替原始矩阵，就可以实现对原始矩阵进行降维，得到数据特征的降维矩阵，从而减少存储空间，减少计算机资源。

2.非负矩阵分解一个示例解释

通过图1中的面部特征提取例子可领略NMF处理数据的方式。最左边的大矩阵由一系列的小图组成，这些小图是分析数据库中包含的2429个脸部图像的结果，每幅图像由19×19个像素组成。传统方法中这样的小图是一幅完整的人脸图像，但是在NMF方法中，每个小图是通过一组基图像乘以一个权重矩阵而产生的面部特征图，经过这样处理的每幅小图像恰好表示了诸如“鼻子”、“嘴巴”、“眼睛”等人脸局部概念特征，这便大大压缩了存放的图像数据量。左边的大矩阵由每幅小图像的19列一起组成矩阵的一列，那样它就是19×19=361行，2429列。这个例子中，NMF方法用基图像来代表眼、眉毛、鼻子、嘴、耳朵、胡子等，它们一起组成了数据库中的脸。这样给人最先的直觉就是它很好地压缩了数据。事实上Lee和Seung在他们的论文中更深入地指出，与人类识别事物的过程相似，NMF也是一种优化的机制，近似于我们的脑分析和存储人脸数据的过程。这个例子中，原图像表示这些局部特征的加权组合，这与人类思维中“局部构成整体”的概念是相吻合的。因此，NMF算法似乎体现了一种智能行为。

3.非负矩阵分解NMF的应用

（1）图像分析  NMF最成功的一类应用是在图像的分析和处理领域

（2）文本聚类，数据挖掘

（3）语音处理

（4）机器人控制

（5）生物医药工程和化学工程