luoguP4206 [NOI2005]聪聪与可可 期望概率DP

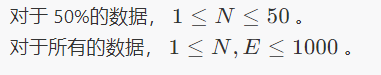
首先，分析一下这个猫和鼠

猫每局都可以追老鼠一步或者两步，但是除了最后的一步，肯定走两步快些....

既然猫走的步数总是比老鼠多，那么它们的距离在逐渐缩小（如果这题只能走一步反而不能做了...）

猫不知道老鼠下一步走哪里，猫走的时候依据的是老鼠当前的位置

明显，猫走的位置没有什么规律可言（即使有规律还是会预处理啊.....）

我们可以在$O(n^2 + nm)$的复杂度内预处理出$s(i, j)$表示猫在$i$，老鼠在$j$时，猫下一步的位置...

直接设$f(i, j)$表示猫在$i$，老鼠在$j$时猫吃到老鼠的期望步数

那么有$f(i, i) = 0$

并且$f(i, s(i, j)) = 1，f(i, s(s(i, j), j)) = 1 (i \neq j)$

其余情况下$f(i, j) = \sum\limits_{v = j | e(j, v)} \frac{f(s(s(i, j), j), v) + 1}{du[j] + 1}$

由于猫鼠距离减小，因此转移具有拓扑序

可以根据猫鼠距离排序转移，也可以直接$dfs$

由于$dfs$好写，因此这里选择$dfs$

复杂度$O(n^2 + nm)$

#include <cstdio>
#include <iostream>
using namespace std;

extern inline char gc() {
    static char RR[], *S = RR + , *T = RR + ;
    if(S == T) fread(RR, , , stdin), S = RR;
    return *S ++;
}
inline int read() {
    int p = , w = ; char c = gc();
    while(c > '' || c < '') { if(c == '-') w = -; c = gc(); }
    while(c >= '' && c <= '') p = p *  + c - '', c = gc();
    return p * w;
}

#define de double
#define sid 1005
#define eid 5005
#define ri register int

int n, m, s, t, cnp;
int cap[eid], nxt[eid], node[eid], q[eid];
int du[sid], dis[sid][sid], nx[sid][sid];
de f[sid][sid];

void adeg(int u, int v) {
    du[u] ++;
    nxt[++ cnp] = cap[u]; cap[u] = cnp; node[cnp] = v;
}

#define cur node[i]
void Pre() {
    for(ri u = ; u <= n; u ++) {
        int fr = , to = ;
        q[++ to] = u; dis[u][u] = ;
        while(fr <= to) {
            int o = q[fr ++];
            for(ri i = cap[o]; i; i = nxt[i])
            if(dis[u][cur] == 1e5)
            dis[u][cur] = dis[u][o] + , q[++ to] = cur;
        }
    }
    for(ri u = ; u <= n; u ++)
    for(ri v = ; v <= n; v ++) {
        int w = 1e5;
        for(ri i = cap[u]; i; i = nxt[i])
        if(dis[cur][v] < w || (dis[cur][v] == w && nx[u][v] > cur))
        nx[u][v] = cur, w = dis[cur][v];
    }
}

de dfs(int a, int b) {
    if(f[a][b] != -) return f[a][b];
    if(a == b) return f[a][b] = ;
    int to = nx[a][b], toto = nx[to][b];
    if(to == b || toto == b) return f[a][b] = ;
    f[a][b] = ;
    for(int i = cap[b]; i; i = nxt[i])
    f[a][b] += (dfs(toto, cur) + ) / (de)(du[b] + );
    f[a][b] += (dfs(toto, b) + ) / (de)(du[b] + );
    return f[a][b];
}

int main() {
    n = read(); m = read();
    s = read(); t = read();
    for(ri i = ; i <= m; i ++) {
        int u = read(), v = read();
        adeg(u, v); adeg(v, u);
    }

    for(ri i = ; i <= n; i ++)
    for(ri j = ; j <= n; j ++)
    dis[i][j] = 1e5, f[i][j] = -;

    Pre();
    printf("%.3lf\n", dfs(s, t));
    return ;
}