DFS与DP算法

名词解释：

DFS(Dynamic Plan)：动态规划

DFS(Depth First Search)：深度优先搜索

DFS与DP的关系

很多情况下，dfs和dp两种解题方法的思路都是很相似的，这两种算法在一定程度上是可以互相转化的。

想到dfs也就常常会想到dp，当然在一些特定的适用场合下除外。

dp主要运用了预处理的思想，而dfs则是类似于白手起家，一步步探索。一般来讲，能够预处理要好些，好比战争前做好准备。

dfs和dp都是十分重要的基础算法，在各个竞赛中都有涉及，务必精通。

---

题目：

The Triangle

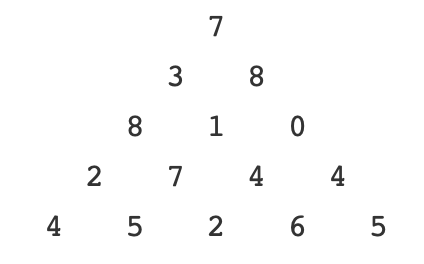
描述：

编写一个程序，计算从顶部开始到底部某处的路径上传递的最大数字总和。 每个步骤可以向左下或右下滑动。

输入：

程序是从标准输入读取。 第一行包含一个整数N：三角形中的行数。 以下N行描述了三角形的数据。 三角形中的行数1<N<=100.三角形中的数字全部为整数，介于0到99之间。

输出：

程序是标准输出。输出最大的整数和。

 样例：

输入：

输出：

---

DFS思路：

自顶向下，将每种路径都走一遍。

通过迭代计算到最后一层，记录最后一层的所有值。最后一层中的最大值即为所求。

具体代码：

 #include <iostream>
 #include <vector>
 #include <algorithm>
 #include <functional>
 using namespace std;

 // the maximum of the triangle ordinal
 const int max_ordinal = ;
 // the depth
 int num_of_rows;
 // save data
 int data[max_ordinal][max_ordinal];
 // save the data of the final level
 vector<int> ans;

 void dfs(int level, int sum, int column)
 {
   // avoid multi calculate
   int current_sum = sum+data[level][column];
   // save data which was in final level
   if(level+ == num_of_rows)
   {
     ans.push_back(current_sum);
     return;
   }
   // binary tree
   dfs(level+, current_sum, column);
   dfs(level+, current_sum, column+);
 }

 int main()
 {
   cin >> num_of_rows;
   for(int i = ; i < num_of_rows; i++)
     for(int j = ; j <= i; j++)
       scanf("%d", &data[i][j]);

   dfs(, , );
   cout << "output data:" << endl;

   sort(ans.begin(), ans.end(), greater<int>());
   for(int i = ; i < ans.size(); i++)
   {
     cout << ans[i] << "\t";
     if(!((i+) % )) cout << endl;
   }
   cout << endl;

   return ;
 }

---

DP思路：

dfs的思路是从上到下，而dp的思路是：从第二层开始，每下去一次往回看一下并取上一层相邻两个大的那个。

具体代码：

 #include <iostream>
 #include <algorithm>
 #include <functional>
 using namespace std;

 // same as DFS
 const int max_ordinal = ;
 int num_of_rows;
 int data[max_ordinal][max_ordinal];
 // the array of the dp method
 int dp[max_ordinal][max_ordinal];

 int main()
 {
     cin >> num_of_rows;
     for(int i = ; i < num_of_rows; i++)
         for(int j = ; j<= i; j++)
             scanf("%d", &data[i][j]);

     // dp now
     dp[][] = data[][];
     for(int i = ; i < num_of_rows; i++)
     {
         for(int j = ; j <= i; j++)
         {
             if(j- >= )
             {
                 dp[i][j] = data[i][j] + max(dp[i-][j], dp[i-][j-]);
             } else {
                 dp[i][j] = data[i][j] + dp[i-][j];
             }
         }
     }

   // calling 'sort' method
     sort(dp[num_of_rows-], &dp[num_of_rows-][num_of_rows], greater<int>());
     for(int i = ; i < num_of_rows; i++)
         cout << dp[num_of_rows-][i] << " ";
     cout << endl;
     cout << "answer is: ";
     cout << dp[num_of_rows-][] << endl;

     return ;
 }