离散傅里叶变换（DFT）

目录 

   一、研究的意义

    二、DFT的定义

   三、DFT与傅里叶变换和Z变换的关系

    四、DFT的周期性

    五、matlab实验

      五.1 程序

         五.2 实验结果

一、研究的意义

DTFT计算公式，中的w取值是连续的而且从负无穷大到正无穷大，对于计算机处理是不可能的，需要无限细分无限区间。即使在DTFT小节中用matlab实现计算，也只是将(-pi,pi)区间划分成1600份来逼近DTFT的效果。

实际上真正用的是DFT，离散傅里叶变换。离散傅里叶变换可以将连续的频谱转化成离散的频谱去计算，这样就易于计算机编程实现傅里叶变换的计算。FFT算法的出现，使得DFT的计算速度更快。

二、DFT的定义

    由上边的定义可知，w=(2*pi/N)*k ,k=0,1,......,N-1，所以w的范围为[0，(N-1/N)*2*pi]。因为是离散取值，实际的区间长度为N，但不含第N个点，w的范围就是[0，2*pi)。

    也就是说DFT变换的频谱范围是在竖轴的右侧（>0），而且取了FT变换的一个周期(0,2*pi)。

三、DFT与傅里叶变换和Z变换的关系

四、DFT的周期性

以下的四个式子，在程序设计和理解程序中经常用到，wd、wa分别为数字角频率和其对应的模拟角频率。

（1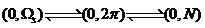），描述了模拟角频率、数字角频率以及DFT变换的k之间的对应关系

（2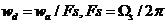），描述了数字角频率与模拟角频率之间的关系

（3），描述了数字角频率和DFT变换的k之间的关系

（4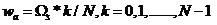），描述了模拟角频率和DFT变换的k之间的关系

五、matlab实验

1、程序

 M=;                         %原离散信号有4点
 n=[::M-];                 %原信号是1行4列的矩阵
 xn=[   ];                %构建原始信号
 subplot(,,);
 stem(n,xn);                  %画图
 title('原始信号');

 N=;                        %16点DFT变换
 k=[::N-];                 %k取值为0,,，···，
 Wn=exp(-j**pi/N);           %求Wn
 X=xn*(Wn.^(n'*k));           %求DFT变换，原始定义的方法，对复指数分量求和而得
 subplot(,,);
 stem(k,abs(X));
 title('原信号的16点DFT变换');

 N1=;                        %8点DFT变换
 k1=[::N1-];               %k取值为0,,，···，
 Wn1=exp(-j**pi/N1);         %求Wn1
 X1=xn*(Wn1.^(n'*k1));        %求DFT变换，采用原始定义的方法，对复指数分量求和而得
 subplot(,,);
 stem(k1,abs(X1));
 title('原信号的8点DFT变换');

说明：

（1）DFT的计算利用的是定义法

（2）程序第10行

程序第11行计算过程

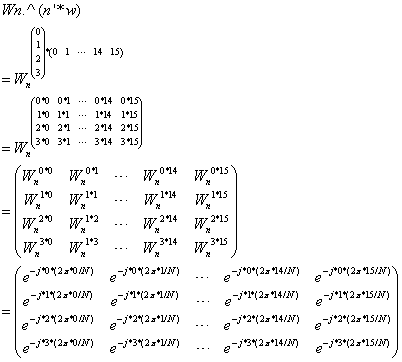
2、实验结果

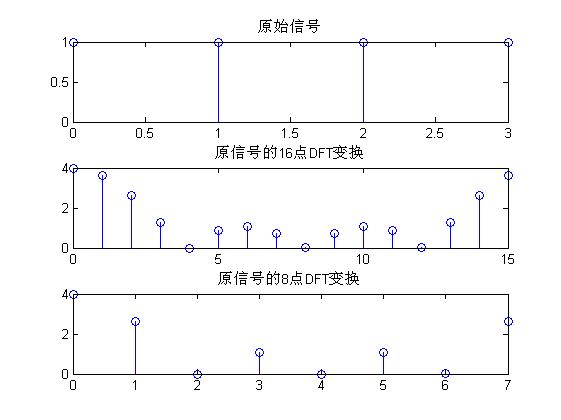
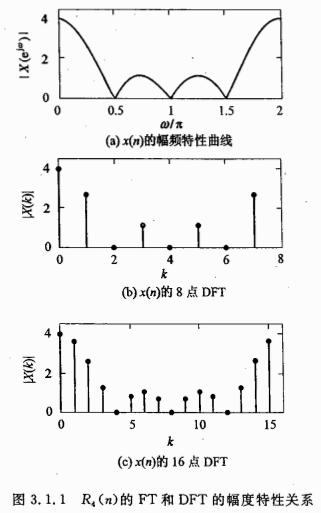
说明：上图结果证明了离散傅里叶变化是对FT变化在区间（0,2*pi）的等间距N点采样。

参考：西电《数字信号处理》第三版

用matlab对信号进行傅里叶变换