BZOJ 4815 CQOI2017 小Q的表格 欧拉函数+分块

题目链接：https://www.lydsy.com/JudgeOnline/problem.php?id=4815

题意概述：要认真概述的话这个题就出来了。。。

分析：

　　首先分析题目，认真研究一下修改操作，想到一个问题：满足什么样的条件的格子会互相影响？

　　看到式子，一想，这正是辗转相除？迅速意识到行列的gcd相同的格子会互相影响。

　　然后我们再利用一下系数的关系，把式子变成f(a,a+b)/(a+b)=f(a,b)/b，发现当行相同的时候格子之间的值与所处列数成正比关系，因为题目保证了f(a,b)=f(b,a)，同样的性质也会出现在列相同的情况下。对于任意两个互相影响的格子，都可以先变换行坐标再变换列坐标互相到达，于是有：f(a,b)/(a*b)=f(x,y)/(x*y)。

　　然后你发现有了这个性质，我们就可以用一维空间来储存所有的格子的值了~

　　令gcd(i,j)=g，那么f(i,j)=f(g,g)*(i*j)/(g*g)。我们令f(g)=f(g,g)，所有格子(i,j)的值都可以由f(gcd(i,j))得到。

　　所以有：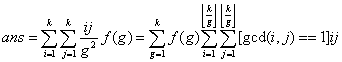

　　我们令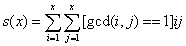：，则

　　考虑一下s(x)的计算，我们枚举i，然后枚举所有小于i的j，如果i,j互质，我们就统计进入答案，可以看成是统计所有小于i且与i互质的j的和乘以i统计进入答案，根据对称性，另一半方阵是一样的，单独处理对角线上的唯一有贡献的(1,1)即可。

　　有一个神奇的公式：小于i且和i互质的正整数的和为phi(i)*i/2（证明：对于一个小于i的x，gcd(i,x)=1，有gcd(i,i-x)=1，也就是说小于i且与i互质的数是成对出现的，并且每一对的和为i，一共有phi(i)/2对）。（对s(x)的计算也可以莫比乌斯反演，借助[gcd(i,j)==1]=[sum{ mu(k) | k|i,k|j,即k|gcd(i,j) }==1]，但是我只探索出了70分的世界线......）

　　所以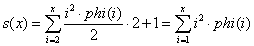：，可以直接预处理出来。

　　最后我们只要用一个分块支持O(sqrt(n))修改，O(1)查询，加上用O(sqrt(k))枚举k的约数就可以做到每组询问O(sqrt(n)+sqrt(k))的时间回答了（有的时候分块的O(1)询问是个很棒的东西，弄个树状数组就自寻烦恼了，分块有点小细节，一定要把f(x)的值原原本本地存起来，不能取模）。

　　时间复杂度O(M(sqrt(N)+sqrt(K)))。

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<algorithm>
 #include<cmath>
 #include<queue>
 #include<set>
 #include<map>
 #include<vector>
 #include<cctype>
 using namespace std;
 const int MAXN=;
 const int mo=;
 typedef long long LL;

 int M,N,K;
 int pri[MAXN],tot,phi[MAXN],s[MAXN];
 bool ntp[MAXN];
 struct Block{
     static const int maxn=;
     static const int size=;
     static const int maxm=;
     int sum[maxn],flag[maxm],L[maxm],R[maxm],cnt,sz,belong[maxn];
     LL f[maxn];
     Block(){ sz=; }
     void build(int n){
         for(sz=;sz+size<n;sz+=size){
             cnt++,L[cnt]=sz,R[cnt]=sz+size;
             for(int j=L[cnt];j<R[cnt];j++)
                 f[j]=1ll*j*j,sum[j]=(sum[j-]+f[j]%mo)%mo,belong[j]=cnt;
             flag[cnt]=;
         }
         cnt++,L[cnt]=sz,R[cnt]=n+;
         for(int j=L[cnt];j<R[cnt];j++)
             f[j]=1ll*j*j,sum[j]=(sum[j-]+f[j]%mo)%mo,belong[j]=cnt;
         flag[cnt]=;
         sz=n;
     }
     void update(int p,LL v){
         int delt=((v-f[p])%mo+mo)%mo;
         f[p]=v;
         for(int i=p;i<R[belong[p]];i++)
             sum[i]=(sum[i]+delt)%mo;
         for(int i=belong[p]+;i<=cnt;i++)
             flag[i]=(flag[i]+delt)%mo;
     }
     int query(int p){
         return (sum[p]+flag[belong[p]])%mo;
     }
 }block;

 void ready()
 {
     ntp[]=ntp[]=,phi[]=;
     for(int i=;i<=N;i++){
         if(!ntp[i]) pri[++tot]=i,phi[i]=i-;
         for(int j=;j<=tot&&1ll*pri[j]*i<=N;j++){
             ntp[pri[j]*i]=;
             if(i%pri[j]==){
                 phi[i*pri[j]]=phi[i]*pri[j];
                 break;
             }
             phi[i*pri[j]]=phi[i]*(pri[j]-);
         }
     }
     block.build(N);
     for(int i=;i<=N;i++)
         s[i]=(s[i-]+1ll*i*i%mo*phi[i]%mo)%mo;
 }
 int gcd(int x,int y){ return !y?x:gcd(y,x%y); }
 void work()
 {
     scanf("%d%d",&M,&N);
     ready();
     int a,b,k,p,ans,d; LL x;
     for(int i=;i<=M;i++){
         scanf("%d%d%lld%d",&a,&b,&x,&k);
         p=gcd(a,b);
         block.update(p,x/(a/p)/(b/p));
         ans=;
         for(int g=,last;g<=k;g=last+){
             last=k/(k/g);
             d=((block.query(last)-block.query(g-))%mo+mo)%mo;
             ans=(ans+1ll*s[k/g]*d%mo)%mo;
         }
         printf("%d\n",ans);
     }
 }
 int main()
 {
     work();
     return ;
 }