一、由线性回归导出逻辑回归：

二、“一对多”算法解决多分类问题：

三、“过拟合”和“欠拟合”：

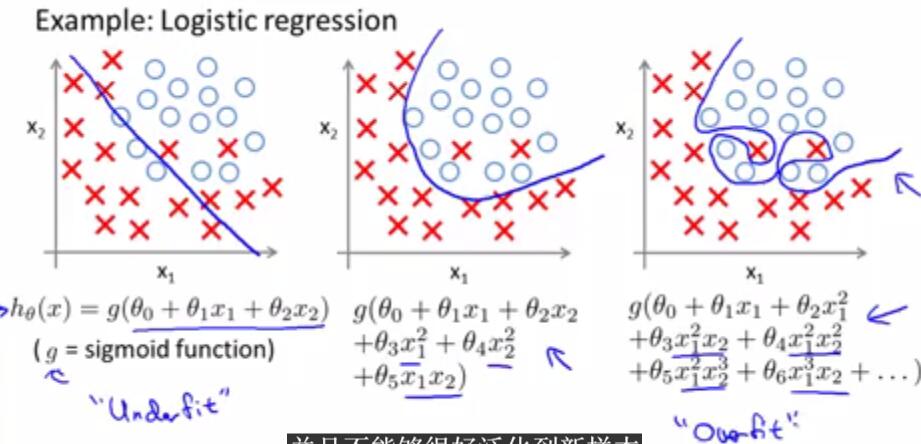
（1）对线性回归加入正则项：

（2）对逻辑回归加入正则项：

（3）加入正则项之后的正规方程：

Andrew Ng在coursera上的ML视频 知识点笔记（2）的更多相关文章

  1. Andrew Ng在coursera上的ML课程_知识点笔记_(1)

    1.Feature Scaling(特征缩放): 如上图所示,x1是房屋面积,x2是房间个数,若不进行特征缩放,则代价函数J的曲线近似为一个瘦长的椭圆(我暂时这么理解,θ1和θ2分别是x1和x2的权值 ...

  2. [Machine Learning] Andrew Ng on Coursera (Week 1)

    Week 1 的内容主要有: 机器学习的定义 监督式学习和无监督式学习 线性回归和成本函数 梯度下降算法 线性代数回归 主要是了解一下机器学习的基本概念,重点是学习线性回归模型,以及对应的成本函数和梯 ...

  3. 【原】Coursera—Andrew Ng斯坦福机器学习（0）——课程地址和软件下载

    斯坦福大学机器学习 课程信息 机器学习是一门研究在非特定编程条件下让计算机采取行动的学科.最近二十年,机器学习为我们带来了自动驾驶汽车.实用的语音识别.高效的网络搜索,让我们对人类基因的解读能力大大提 ...

  4. Andrew Ng 的 Machine Learning 课程学习 (week5) Neural Network Learning

    这学期一直在跟进 Coursera上的 Machina Learning 公开课, 老师Andrew Ng是coursera的创始人之一,Machine Learning方面的大牛.这门课程对想要了解 ...

  5. Andrew Ng 的 Machine Learning 课程学习 (week4) Multi-class Classification and Neural Networks

    这学期一直在跟进 Coursera上的 Machina Learning 公开课, 老师Andrew Ng是coursera的创始人之一,Machine Learning方面的大牛.这门课程对想要了解 ...

  6. Andrew Ng 的 Machine Learning 课程学习 (week3) Logistic Regression

    这学期一直在跟进 Coursera上的 Machina Learning 公开课, 老师Andrew Ng是coursera的创始人之一,Machine Learning方面的大牛.这门课程对想要了解 ...

  7. Andrew Ng 的 Machine Learning 课程学习 (week2) Linear Regression

    这学期一直在跟进 Coursera上的 Machina Learning 公开课, 老师Andrew Ng是coursera的创始人之一,Machine Learning方面的大牛.这门课程对想要了解 ...

  8. 机器学习笔记(一)- from Andrew Ng的教学视频

    最近算是一段空闲期,不想荒废,记得之前有收藏一个机器学习的链接Andrew Ng的网易公开课,其中的overfiting部分做组会报告时涉及到了,这几天有时间决定把这部课程学完,好歹算是有个粗浅的认识 ...

  9. 【原】Coursera—Andrew Ng机器学习—编程作业 Programming Exercise 4—反向传播神经网络

    课程笔记 Coursera—Andrew Ng机器学习—课程笔记 Lecture 9_Neural Networks learning 作业说明 Exercise 4,Week 5,实现反向传播 ba ...

随机推荐

  1. （python爬取小故事网并写入mysql）

    前言: 这是一篇来自整理EVERNOTE的笔记所产生的小博客,实现功能主要为用广度优先算法爬取小故事网,爬满100个链接并写入mysql,虽然CS作为双学位已经修习了三年多了,但不仅理论知识一般,动手 ...

  2. android限制横竖屏切换 方法

    在需要限制横竖屏切换的时候,只需要在AndroidManifest.xml文件中加入android:screenOrientation属性限制. android:screenOrientation=& ...

  3. [luogu4551][POJ3764]最长异或路径

    题目描述 给定一棵n个点的带权树,结点下标从1开始到N.寻找树中找两个结点,求最长的异或路径. 异或路径指的是指两个结点之间唯一路径上的所有边权的异或. 分析 处理出各个节点到根节点的异或距离,然后我 ...

  4. BFS求解迷宫的最短路径问题

    题目:给定一个大小为N*M的迷宫,迷宫由通道('.')和墙壁('#')组成,其中通道S表示起点,通道G表示终点,每一步移动可以达到上下左右中不是墙壁的位置.试求出起点到终点的最小步数.(本题假定迷宫是 ...

  5. 逆向---03.mov、test等汇编指令、EAX、关键Call、OD调试技巧

    上一篇:逆向---02.je & jmp & jnz .OD调试 基础知识:(栗子中也会说的)栗子:链接: https://pan.baidu.com/s/1qZbbTvQ 密码: i ...

  6. Logstash grok解析IIS 10.0 日志实例

    Logstash解析IIS日志的核心在于logstash配置文件 IIS 日志位置和格式如下: #Software: Microsoft Internet Information Services 1 ...

  7. C# 面向对象零碎知识点

    obgect: 所有数据类型都是obgect类型: 万能类型 var :原来的变量不变,替换成var: 动态类型 dynamic :类似object,遍历需要转: is  as: 类型转换运算符: ( ...

  8. P1963 [NOI2009]变换序列

    对于\(N\)个整数\(0, 1, \cdots, N-1,\)一个变换序列\(T\)可以将\(i\)变成\(T_i\),其中 \(T_i \in \{ 0,1,\cdots, N-1\}\)且 \( ...

  9. 2636652995 揭秘骗子qq

    3042952272636652995755610392020068008这是个骗子群526875508,群里都是群主的小号,付钱之后不给东西,还在群里维护骗子的利益,很明显了.都是骗子小号了,付完整 ...

  10. mock.js的使用

    安装 npm install mockjs 使用 const Mock = require("mockjs") //格式"属性名|min-max": " ...