洛谷 P1357 花园 解题报告

P1357 花园

题目描述

小\(L\)有一座环形花园，沿花园的顺时针方向，他把各个花圃编号为\(1~N(2<=N<=10^{15})\)。他的环形花园每天都会换一个新花样，但他的花园都不外乎一个规则，任意相邻\(M(2<=M<=5,M<=N)\)个花圃中有不超过\(K(1<=K<M)\)个\(C\)形的花圃，其余花圃均为\(P\)形的花圃。

例如，\(N=10,M=5,K=3\)。则

\(CCPCPPPPCC\)是一种不符合规则的花圃；

\(CCPPPPCPCP\)是一种符合规则的花圃。

请帮小\(L\)求出符合规则的花园种数\(Mod\) 1000000007

由于请您编写一个程序解决此题。

输入输出格式

输入格式：

一行，三个数\(N,M,K\)。

输出格式：

花园种数\(Mod\) 1000000007

说明

40%的数据中，\(N<=20\)；

60%的数据中，\(M=2\)；

80%的数据中，\(N<=10^5\)。

100%的数据中，\(N<=10^{15}\)。

---

这道题的思维难度是真的大（也可能是我菜）

请顺着看（我就是因为直接看别人题解没彻底理解前面的就去往后翻导致理解了很久）

---

80分给了状压DP

不考虑环时

令\(dp[i][j]\)代表当进行到第\(i\)个位置时，前\(M\)位的状态为\(j\)

\(dp[i][j]=dp[i-1][k]\),\(k\)为合法的前一位状态。

关于状压的思路，有两个导向性。

(1) \(2<=M<=5\)

(2) 当进行转移时，要想知道合不合法得知道前\(M\)位上的所有数。

---

当然，如果想不到如何处理环，状压的80分也白瞎。

想想在状压中，我们的状态实质上是一个区间，我们进行递推的时候，实际上相当于把这个区间向右滑动。

如果我们这时候只对一个初始合法区间\(j_0\)进行移动，当移动了\(n\)次以后，它可能到达很多个状态。但是如果它和自己重合了，不就连成了一个环了吗？

这时候\(dp[n][j_0]\)就代表只移动合法区间\(j_0\)所构成的环的方案数。

我们把每个初始合法区间都做一次这样的状压\(DP\)，统计答案。

复杂度:\(O(M!^3*N)\)

当然实际上我们通过预处理，可以得到类似\(dx[i][j]\)这样的数组，表示状态\(i\)是否可以到达状态\(j\)。使复杂度远远达不到上界。

---

我们发现，\(N\)的长度和\(dx[i][j]\)没有什么关系，而\(dx[i][j]\)又是一个矩阵。

那么当忽略\(i\)这一维度时，\(dp[j]\)通过\(dx[i][j]\)向后一位进行递推，不就是矩阵乘法吗？

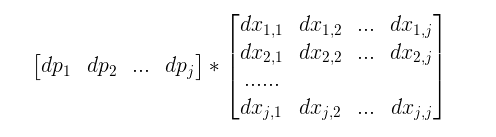
左边是推到某一位了，和右边矩阵相乘得到下一位。

可以直接用矩阵快速幂求解可达性矩阵的\(N\)次方，然后与每一个初始合法状态相乘。

我们发现，可达性矩阵和第\(j\)个状态的初始矩阵进行相乘后，只能取\((j,j)\)位置的值，所以最终的答案即是可达性矩阵乘方后对角线值之和。

---

Code:

#include <cstdio>
#include <cstring>
#define ll long long
const int N=123;
const ll mod=1e9+7;
ll n;
int m,k,len;
struct matrix
{
    ll dx[N][N];
    matrix()
    {
        memset(dx,0,sizeof(dx));
    }
    matrix friend operator *(matrix n1,matrix n2)
    {
        matrix n3;
        for(int i=0;i<=len;i++)
            for(int j=0;j<=len;j++)
                for(int k=0;k<=len;k++)
                    n3.dx[i][j]=(n3.dx[i][j]+n1.dx[i][k]*n2.dx[k][j])%mod;
        return n3;
    }
}d,f;
bool check(int x)
{
    int cnt=k;
    while(x)
    {
        cnt--;
        x-=x&-x;
    }
    return cnt>=0;
}
void init()
{
    scanf("%lld%d%d",&n,&m,&k);//m中不超过k个1
    len=(1<<m)-1;
    for(int i=0;i<=len;i++)
    {
        if(!check(i))
            continue;
        int to=(i<<1)&len;
        if(!check(to))
            continue;
        d.dx[to][i]=1;
        to=to|1;
        if(!check(to))
            continue;
        d.dx[to][i]=1;
    }
    for(int i=0;i<=len;i++)
        f.dx[i][i]=1;
}
void quick_pow()
{
    while(n)
    {
        if(n&1)
            f=f*d;
        d=d*d;
        n>>=1;
    }
}
void work()
{
    quick_pow();
    ll ans=0;
    for(int i=0;i<=len;i++)
        ans=(ans+f.dx[i][i])%mod;
    printf("%lld\n",ans);
}
int main()
{
    init();
    work();
    return 0;
}

---

2018.7.2