hdu 6141 I am your Father!

题

　　OvO http://acm.hdu.edu.cn/showproblem.php?pid=6141

　　（2017 Multi-University Training Contest - Team 8 - 1009）

解　

　　首先这是一个有向图，所以使用最小树形图算法。

　　然后题目要求的是节点n的父亲节点的值最小，

　　那么，可以把全部边的值乘以1000，如果这条边的终止点是节点n的话，设这条边的起始点为u，那么边值加上（999-u），这样就能保证优先取字典序小的，

　　然后由于题目要求的是最大的，所以可以把边的值取倒数。

　　

　　至于最小树形图算法，

　　1. 找当前图每个节点的非自环最小入边，

　　2. 如果当天图存在环：把环缩成点，然后构造一张新图，返回步骤1,（至于如何构造，见下图）

　　　否则结束　　

　　这张图我复制的（我感觉这张图超好懂来着），来源：O∧O （貌似来源处这张图也是复制的）

　　

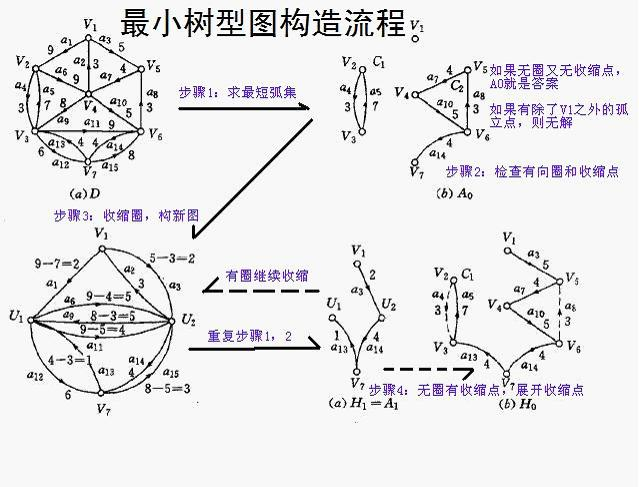
　　（思路来自题解）

#include<iostream>
#include<cstdio>
#include<cstring>
#define MAXN 1005
#define INF 0x7f7f7f7f
using namespace std;
typedef long long ll;
struct node
{
    int u, v;
    ll w;
}edge[MAXN * MAXN];
int pre[MAXN], id[MAXN], vis[MAXN], n, m, pos;
int ans_father;
ll in[MAXN];
ll Directed_MST(int root, int V, int E)	//边、点全是从0开始计算的
{
    ll ret = 0;//存最小树形图总权值
    while(true)
    {
		int i;
		//1.找每个节点的最小入边
        for( i = 0; i < V; i++)
            in[i] = INF;//初始化为无穷大
        for( i = 0; i < E; i++)//遍历每条边
        {
            int u = edge[i].u;
            int v = edge[i].v;
            if(edge[i].w < in[v] && u != v)//说明顶点v有条权值较小的入边  记录之
            {
                pre[v] = u;//节点u指向v
                in[v] = edge[i].w;//最小入边
                if(u == root)//这个点就是实际的起点
					pos = i;
            }
        }
        for( i = 0; i < V; i++)//判断是否存在最小树形图
        {
            if(i == root)
				continue;
            if(in[i] == INF)
				return -1;//除了根以外有点没有入边,则根无法到达它  说明它是独立的点 一定不能构成树形图
        }
        //2.找环
        int cnt = 0;//记录环数
        memset(id, -1, sizeof(id));
        memset(vis, -1, sizeof(vis));
        in[root] = 0;
        for( i = 0; i < V; i++) //标记每个环
        {
            ret += in[i];//记录权值
            int v = i;
            while(vis[v] != i && id[v] == -1 && v != root)
            {
                vis[v] = i;
                v = pre[v];
            }
            if(v != root && id[v] == -1)
            {
                for(int u = pre[v]; u != v; u = pre[u])
                    id[u] = cnt;//标记节点u为第几个环
                id[v] = cnt++;
            }
        }
        if(cnt == 0)
			break; //无环   则break
        for( i = 0; i < V; i++)
            if(id[i] == -1)
				id[i] = cnt++;
			//3.建立新图   缩点,重新标记
			for( i = 0; i < E; i++)
			{
				int u = edge[i].u;
				int v = edge[i].v;
				edge[i].u = id[u];
				edge[i].v = id[v];
				if(id[u] != id[v])
					edge[i].w -= in[v];
			}
			V = cnt;
			root = id[root];
    }
    return ret;
}
int main()
{
//	freopen("数据\\1009.in","r",stdin);
//	freopen("数据\\fxxl1009.out","w",stdout);
	int i,j,cas;
	scanf("%d",&cas);
    while(cas--)
    {
    	scanf("%d%d",&n,&m);
        for(i=0;i<m;i++)
        {
            scanf("%d%d%lld", &edge[i].u, &edge[i].v, &edge[i].w);
            edge[i].u--; edge[i].v--;
            edge[i].w*=1000;
            if(edge[i].v==n-1)
            	edge[i].w+=(999-edge[i].u);
            edge[i].w*=-1;
		}
        ll ans = Directed_MST(0,n,m);
//        cout<<ans<<' '<<ans_father<<endl;
		ans*=-1;
        ans_father=(999-ans%1000)+1;
        ans=ans/1000;
		printf("%lld %d\n",ans,ans_father);
    }
    return 0;
}

/*

1
3 8
1 2 10
2 1 10
2 3 10
3 2 10
1 3 10
3 1 10
2 1 100
3 1 100

*/