梯度下降(Gradient Descent)小结 -2017.7.20

在求解算法的模型函数时，常用到梯度下降(Gradient Descent)和最小二乘法，下面讨论梯度下降的线性模型(linear model)。

1.问题引入

给定一组训练集合(training set)yi，i = 1,2,...,m，引入学习算法参数(parameters of learning algorithm)θ1，θ2，.....，θn，构造假设函数(hypothesis function)h(x)如下：

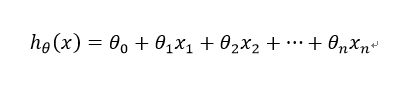
定义x0 = 1，则假设函数h(x)也可以记为以下形式：

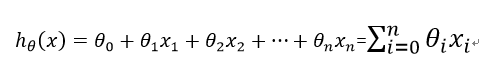
这里xi（i = 1,2,...,n）称为输入特征(input feature)，n为特征数。

对于训练集合yi，要使假设函数h(x)拟合程度最好，就要使损失函数(loss function)J(θ)达到最小，J(θ)表达式如下：

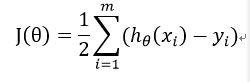
2.问题推导

目标是使J(θ)达到最小，此时的θ值即为所求参数，首先来看梯度下降的几何形式。

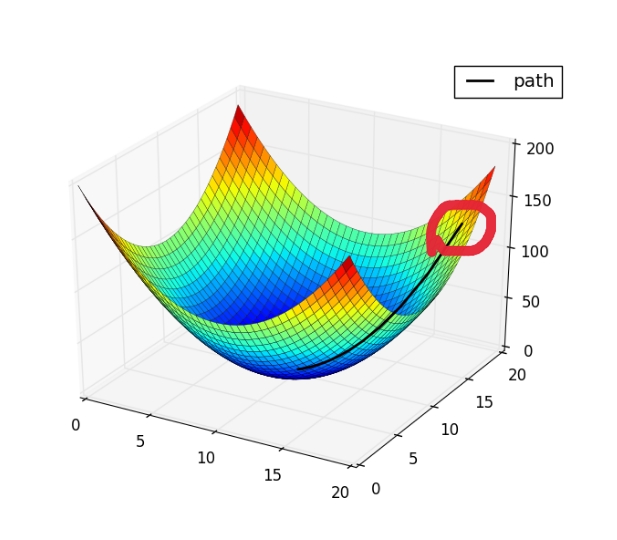
（1）梯度下降的几何形式

上图圈内点为初始设置的参考点，想象这是一座山的地形图，你站在参考点上准备下山，要从哪里走，下山的速度最快？选择一个方向，每次移动一小点步伐，直到移动到图正下方的蓝色区域，找到了局部最优解。显然，对于此图来说，设置的初始参考点不同，找到的局部最优解也不同。其实，真正的J(θ)大部分是如下图的形状，只有一个全局最优解：

（2）批量梯度下降(Batch Gradient Descent)法

方法是对θi进行多次迭代，迭代减去速率因子α(learning rate)乘以J(θ)对θi的偏导数。

下面推导过程取m = 1的特殊情况，即只有一个训练样本，并逐步推导至一般过程。

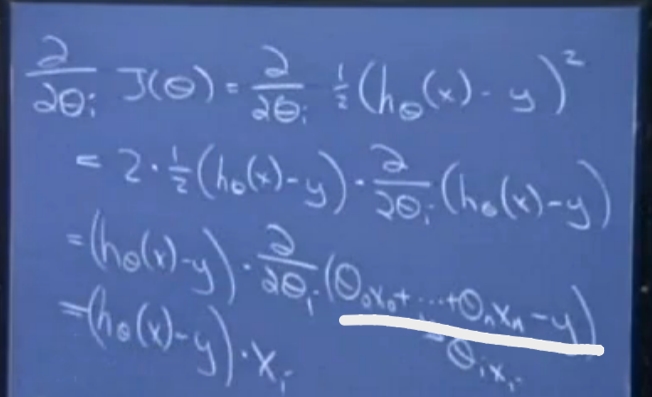
划线部分只有θixi与θi有关，得到的θi迭代表达式为：

推广至m个训练样本，则迭代表达式为：

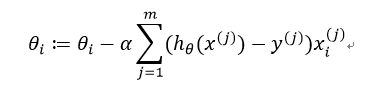
但批量梯度下降的每一次迭代都要遍历所有训练样本，不适用于训练样本数量极多的情况，于是提出了随机梯度下降(Stochastic Gradient Descent)法

（3）随机梯度下降(Stochastic Gradient Descent)法

每次都只使用第j个样本，速度比批量梯度下降快了很多。

（4）两种梯度下降方法比较

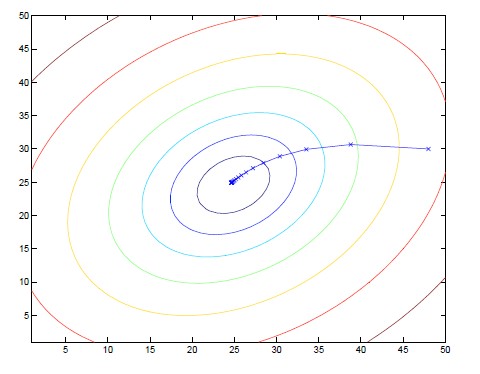
下面是两种梯度下降算法的迭代等高图

批量梯度下降：

随机梯度下降（紫色线所示）：

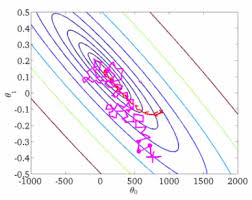
随机梯度下降的每次迭代，有可能变大或变小，但总体趋势接近全局最优解，通常参数值会十分接近最小值。

3.注意事项

（1）α的取值不宜太大或太小。

if α is too small then will take very tiny steps and take long time to converge;

if α is too large then the steepest descent may end up overshooting the minimum.

（2）由于向最优解收敛过程中偏导数会逐渐变小，收敛至最小值时偏导为0，则θi会逐渐变小，因此不需要改变α使其越来越小。

（3）α的取值需要不断测试更改，直至达到效果最好的α。

（4）当梯度下降到一定数值后，每次迭代的变化很小，这时可以设定一个阈值，只要变化小于该阈值，就停止迭代，而得到的结果也近似于最优解。

图片来源：百度

参考博客：http://www.cnblogs.com/ooon/p/4947688.html