【UR #7】水题走四方

题目描述

今天是世界水日，著名的水题资源专家蝈蝈大臣发起了水题走四方活动，向全世界发放成千上万的水题。

蝈蝈大臣是家里蹲大学的教授，当然不愿意出门发水题啦！所以他委托他的助手欧姆来发。

助手欧姆最近做 UR #6 被狗狗传染了懒癌，当然不愿意出门发水题啦！所以他请来了高手 —— 地卜师。

全世界一共 n 个城市，编号分别为 1,…,n。城市之间由双向道路相连，形成了一棵树。如果这棵树以 1 为根，则除 1 以外每个结点 v 的父亲结点的编号 pv 满足 pv<v。

由于地卜师掌握了克隆的核心科技，把自己完全复制了一份，他和他的分身一共两个地卜师一起出去执行任务。

现在，两个地卜师都站在 1 号城市。地卜师可以沿道路行走，从一个城市移动到另一个城市。走一条道路需要耗时 1 小时。当然，地卜师可以停留在某个城市不动。每到一个没有发放水题的城市，地卜师都会发水题。在一个城市里发水题的时间不计。

由于地卜师有强迫症，他沿道路移动时总是从一个城市移动到编号更大的城市。即总是从一个结点移动到它的儿子结点。地卜师和他的分身可以同时移动。

但是地卜师这样好像不一定能经过所有的城市？没关系！地卜师会瞬移。如果某个时刻两个地卜师都在某个城市里（而不是在去某个城市的道路上），那么其中一个地卜师可以瞬移到另一个地卜师所在的城市。瞬移所需的时间不计。

现在地卜师想知道，要想顺利给每个城市都发放水题，最短需要多少个小时。

欧姆当然知道怎么计算啦！但是他想考考你。

题解 

神仙题.png。

我们可以先考虑最优解是怎么走出来的。

先是这个人和它的分身，初步的想法是他们俩来到了一个节点，然后分身去遍历这颗子树的一些儿子中的叶子结点。

最后剩一个儿子，然后它俩一块走到下一个儿子里面。

但是这种想法少考虑了一些情况(反例就不说了，也就是说不能只考虑往儿子走)。

我们可以将两个人同时停留的地方称作关键点，显然所有的关键点都在一条链上。

那么分身应该遍历这颗子树减去下一颗关键点所在子树的那颗子树的所有叶子结点。

就是在分身遍历最后一个叶子的时候，这个人可以同时往下一个关键点走，等到两个人都到了自己该到的地方，分身再TP到这个人那里。

然后有一个初步的dp想法，就是设dp[i]表示i是一个关键点，两个人第一次到这个点所用的最小时间。

转移：

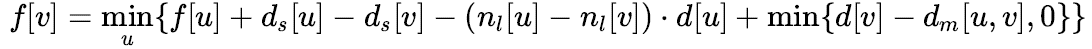
nl：当前子树内的叶子节点个数，ds：当前子树内叶子结点的深度和，dm[u][v]：u的子树扣掉v的子树后最深的叶子结点的深度，d：节点深度。

更正：上面的第二个min为max。

后面那个东西是在讨论这个人和分身谁先到目的地。

这个dp是n^2的，好像有各种高科技的优化办法然而并不会。。。

我们发现这个式子前面那一坨好像可优化性不大。

考虑后面那个max可不可以为0，那么相当于是说找到一个祖先u使得d[v]<=dm[u,v]。

如果我们对于每个点都找出这个祖先的话，转移就轻松完成了。

我们考虑是不是所有点都能找到这个祖先，肯定不是的，当一个点的deep满足没有其他点和它deep相等时这个点是没有这种祖先的。

这样的点有什么神奇的规律？它们是连续的一条链，就是这个样子的。

一棵树下面多出来的这条链。

因为我们是在叶子的位置统计答案，那么有结论，最优解肯定不在这种叶子上(想想为什么)。

那么我们的任务就变成找这种神奇祖先了。

首先这种神奇祖先肯定是越低越好。

我们可以维护一个链表表示还没找到祖先的节点，在子树合并的时候互相更新一下(因为两颗子树的maxdeep都可以作为更新答案的条件)。

这是最多只会有一颗子树内有节点没有找到祖先(想想为什么)，所以我们维护的复杂度是线性的。

代码

#include<iostream>
#include<cstdio>
#define N 5000009
#define inf 1e18
using namespace std;
typedef long long ll;
inline ll rd(){
    ll x=;char c=getchar();bool f=;
    while(!isdigit(c)){if(c=='-')f=;c=getchar();}
    while(isdigit(c)){x=(x<<)+(x<<)+(c^);c=getchar();}
    return f?-x:x;
}
ll n,deep[N],mx_deep[N],sum_deep[N],cnt[N],dp[N];
int nxt[N],up[N],son[N],tot,fa[N];
char s[N<<];
int main(){
    n=rd();
    scanf("%s", s);int v;
    for(int i=;i<n*;i++){
      if(s[i]=='('){
        tot++;
        fa[tot]=v;
        v=tot;
      }
      else v=fa[v];
    }
    for(int i=;i<=n;++i){
        if(fa[i])son[fa[i]]++;
        deep[i]=deep[fa[i]]+;
    }
    for(int i=n;i>=;--i){
        if(!son[i]){
            mx_deep[i]=sum_deep[i]=deep[i];
            cnt[i]=;
        }
        int now=i;
        while(now&&deep[now]<=mx_deep[fa[i]]){
            up[now]=fa[i];
            now=nxt[now];
        }
        while(nxt[fa[i]]&&deep[nxt[fa[i]]]<=mx_deep[i]){
            up[nxt[fa[i]]]=fa[i];
            nxt[fa[i]]=nxt[nxt[fa[i]]];
        }
        if(now)nxt[fa[i]]=now;
        mx_deep[fa[i]]=max(mx_deep[fa[i]],mx_deep[i]);
        sum_deep[fa[i]]+=sum_deep[i];
        cnt[fa[i]]+=cnt[i];
    }
    ll ans=inf;
    for(int i=;i<=n;++i){
        dp[i]=inf;
        if(up[i])dp[i]=dp[up[i]]+sum_deep[up[i]]-sum_deep[i]-(cnt[up[i]]-cnt[i])*deep[up[i]];
        if(son[fa[i]]==)dp[i]=min(dp[fa[i]]+,dp[i]);
        if(!son[i])ans=min(ans,dp[i]);
    }
    if(n==){puts("");return ;}
    cout<<ans;
    return ;
}