Unity3D 中 用quaternion 来对一个坐标点进行旋转的初步体会

在unity3d中,用四元数来表示旋转,四元数英文名叫quaternion . 比如 transform.rotation 就是一个四元数,其由四个部分组成

Quaternion = (xi + yj + zk + w ) = (x,y,z,w)

1.  http://en.wikipedia.org/wiki/Quaternion  有四元数的定义
     2.  http://en.wikipedia.org/wiki/Quaternions_%26_spatial_rotation   有关四元数旋转方面的基本概念和用法
     quaternion 中 (x,y,z) 跟旋转轴有关, w 与绕旋转轴旋转的角度有关,因为它们都要经过代数运算才能得出旋转轴和旋转角度

                    

                      

                    

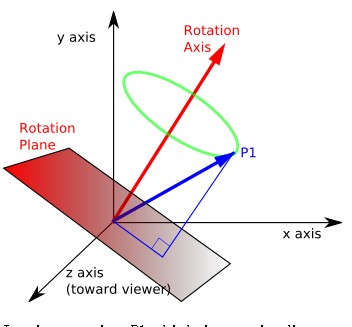
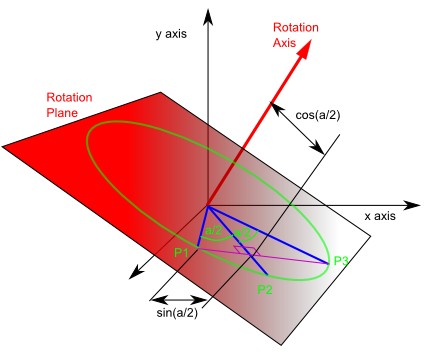
在unity3d中, quaternion 的乘法操作 (operator  * ) 有两种操作:
     (1) quaternion * quaternion , 例如 q = t * p; 这是将一个点先进行t 操作旋转,然后进行p操作旋转.
     (2)  Quaternion * Vector3, 例如 p : Vector3, t : Quaternion , q : Quaternion;    q = t * p; 这是将点p 进性t 操作旋转;
     我进行的是第2种操作,即对一个向量进行旋转;
     首先 ,Quaternion 的基本数学方程为 : Q = cos (a/2) + i (x * sin(a/2)) + j (y * sin(a/2)) + k(z * sin(a/2))    (a 为旋转角度)
      Q.w = cos (angle / 2) 
      Q.x = axis.x * sin (angle / 2) 
      Q.y = axis.y * sin (angle / 2)  
      Q.z = axis.z * sin (angle / 2)
     我们只要有角度就可以给出四元数的四个部分值,例如我想要让点M=Vector3(o,p,q) 绕x轴顺时针旋转90度;那么对应的quaternion数值就应该为:
     Q : Quaternion;
     Q.x = 1 * sin(90度/2) = sin(45度) = 0.7071
     Q.y = 0;
     Q.z = 0;
     Q.w = cos(90度/2) = cos (45度) = 0.7071
     Q = (0.7071, 0 , 0 , 0.7071);
     m = Q * m;         （将点m 绕 x轴(1,0,0) 顺时针旋转了90度)

1. <span style="font-size:12px;">    var m : Vector3;
2. var t1 : Quaternion;
3. m = Vector3(1,0,0);
4. t1 = Quaternion(0.7,0,0,0.7);
5. m = t1*m;</span>

        这是quaternion 的最基本用法,主要给出角度，就可以算出Quaternion，然后对点坐标进行旋转。