P3195 [HNOI2008]玩具装箱TOY 斜率优化dp

传送门：https://www.luogu.org/problem/P3195

题目描述

P教授要去看奥运，但是他舍不下他的玩具，于是他决定把所有的玩具运到北京。他使用自己的压缩器进行压缩，其可以将任意物品变成一堆，再放到一种特殊的一维容器中。P教授有编号为 1\cdots N1⋯N 的 NN 件玩具，第 ii 件玩具经过压缩后变成一维长度为 C_iCi .为了方便整理，P教授要求在一个一维容器中的玩具编号是连续的。同时如果一个一维容器中有多个玩具，那么两件玩具之间要加入一个单位长度的填充物，形式地说如果将第 ii 件玩具到第 jj 个玩具放到一个容器中，那么容器的长度将为 x=j-i+\sum\limits_{k=i}^{j}C_kx=j−i+k=i∑jCk 制作容器的费用与容器的长度有关，根据教授研究，如果容器长度为 xx ,其制作费用为 (X-L)^2(X−L)2 .其中 LL 是一个常量。P教授不关心容器的数目，他可以制作出任意长度的容器，甚至超过 LL 。但他希望费用最小.

感谢@ACの666 提供的Latex题面

输入格式

第一行输入两个整数N，L.接下来N行输入Ci.1<=N<=50000,1<=L,Ci<=10^7

输出格式

输出最小费用

输入输出样例

输入 #1复制

输出 #1复制

先来梳理一下题意吧

就是说有n个玩具要放到好多个容器里（容器个数不限）

使得所花费的费用最小

那么每个容器的费用就是 (X-L)^2 容器长度为x 另外输入时还告诉你一个L

。。。。。

天哪看起来好难的样子

很显然这一道题要是暴力搜索肯定是拿不了几分

做法一：朴素做法

事实上朴素算法还是不错的

就是说 i：1-n j：1-i

dp [ i ] = min ( dp [ j -1] +( sum [ i ] - sum [ j-1 ] + i - j - L )²)

啊啊啊那是什么东西

就是说dp[i]就表示前i个玩具

就是说 sum [ i ] - sum [ j-1 ] + i - j 这个肯定非常好理解题目中已经说就是那个X

“那么每个容器的费用就是 (X-L)^2 容器长度为x 另外输入时还告诉你一个L”

那么很明显这个就没有什么问题啦

感觉这个还是不错

但是：：这是n²的做法啊啊啊啊啊

先写一下试试吧

p.s.才20分。。。呜呜呜

然后就开始一脸发蒙了

斜率优化开始

斜率优化是什么？

不知道···

就是说

首先一次函数肯定知道吧（不知道查一下）

y=kx+b

知识大普及 k是斜率 b是截距

and then 知道又有啥用。。。

我们上面不是得到的一个式子吗我们可以把它转化一下使得它不超时

dp [ i ] = min ( dp [ j -1] +( sum [ i ] - sum [ j-1 ] + i - j - L )²)

然后那可以把这个式子拆一下

我们令a[i]=sum[i]+i

令b[j]=sum[j-1]+j+L; 郑重声明这个是可以预处理出来的（其实无所谓）

这样子接下来可能会好受一点

先把min去了吧这样比较好看一些

dp [ i ] = dp [ j -1] +( sum [ i ] - sum [ j-1 ] + i - j - L ) ²

dp [ i ] = dp[ j -1] +( a[i]-b[j])²

dp[i]=dp[j-1]+a[i]²+b[j]²-2*a[i]*b[j];

2*a[i]*b[j]+dp[i]=dp[j-1]+a[i]²+b[j]^2;

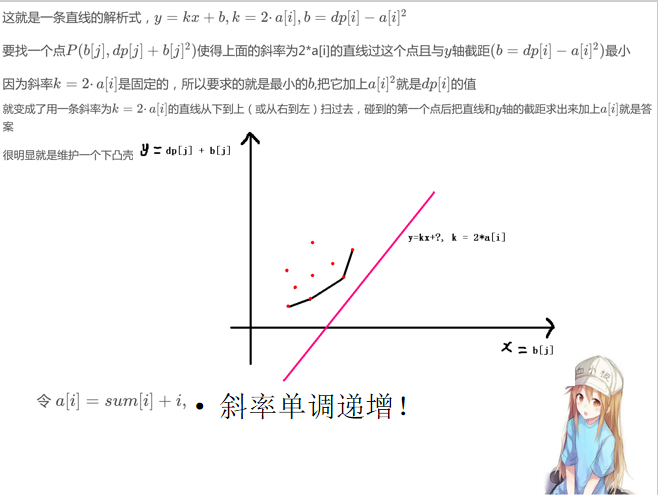
假设x=b[j] y=dp[j-1]+b[j]²

首先你要先明确看到这里没有问题

2*a[i]*x+dp[i]=y+a[i]²

y=2*a[i]*x+dp[i]-a[i]²;

嗯嗯嗯呃

然后干嘛先自己晕一会

啊哈！

y=kx+b

和上面的那个式子对照一下会发现一个非常神奇的事情

k:2*a[i]

b:dp[i]-a[i]²

enenen别跑偏了我们要求的是dp[i]对吧就是那个b里面的

因为a[i]²是固定的对吧（那还用你说。。）

也就是说！！！！！！！求出来最小的b也就能求出来最小的dp[i]

算了讲到这里已经讲不下去了

还是来粘贴一段接下来的讲解吧我只负责讲一下怎么转化为函数表达式啦

#include<bits/stdc++.h>

using namespace std;

const int maxn=;

#define int long long

#define u32 unsigned

int f[maxn],g[maxn];

u32 n,L,q[maxn];

int SQR(int x){

    return x*x;

}

double Get(u32 j,u32 k){

    return ((f[j]+SQR(g[j])+*L*g[j])-(f[k]+SQR(g[k])+*L*g[k]))/(double)(g[j]-g[k]);

}

signed main(){

    scanf("%u%u",&n,&L);

    L++;

    u32 i,j,s,t,K;q[s=t=]=;

    for(i=;i<=n;i++)

        scanf("%lld",&g[i]),g[i]+=g[i-];//维护前缀和（很显然这会更方便啊）

    for(i=;i<=n;i++) g[i]+=i;//就是讲解中 的那个a[i]

    for(i=;i<=n;q[++t]=i++){//我也是第一次发现这么一个神奇的写法   q就是维护了一个单调队列

        K=g[i]<<;//斜率 k=2*a[i]

        while(s<t&&Get(q[s+],q[s])<=K) s++; //找到能形成最小值的点

        j=q[s];f[i]=f[j]+SQR(g[i]-g[j]-L);

        while(s<t&&Get(q[t],q[t-])>=Get(i,q[t])) t--;//维护凸包

    }

    printf("%lld\n",f[n]);

    return ;

}