luogu P2296 寻找道路

题目描述

在有向图G 中，每条边的长度均为1 ，现给定起点和终点，请你在图中找一条从起点到终点的路径，该路径满足以下条件：

1 ．路径上的所有点的出边所指向的点都直接或间接与终点连通。

2 ．在满足条件1 的情况下使路径最短。

注意：图G 中可能存在重边和自环，题目保证终点没有出边。

请你输出符合条件的路径的长度。

输入输出格式

输入格式：

输入文件名为road .in。

第一行有两个用一个空格隔开的整数n 和m ，表示图有n 个点和m 条边。

接下来的m 行每行2 个整数x 、y ，之间用一个空格隔开，表示有一条边从点x 指向点y 。

最后一行有两个用一个空格隔开的整数s 、t ，表示起点为s ，终点为t 。

输出格式：

输出文件名为road .out 。

输出只有一行，包含一个整数，表示满足题目᧿述的最短路径的长度。如果这样的路径不存在，输出- 1 。

输入输出样例

输入样例#1：

3 2
1 2
2 1
1 3

输出样例#1：

-1

输入样例#2：

6 6
1 2
1 3
2 6
2 5
4 5
3 4
1 5

输出样例#2：

3

说明

解释1：

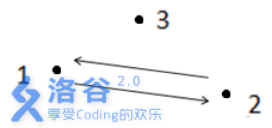
如上图所示，箭头表示有向道路，圆点表示城市。起点1 与终点3 不连通，所以满足题

目᧿述的路径不存在，故输出- 1 。

解释2：

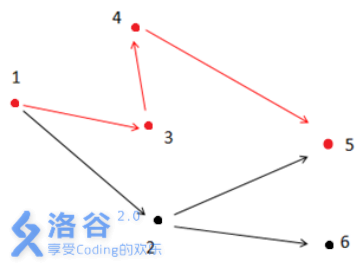
如上图所示，满足条件的路径为1 - >3- >4- >5。注意点2 不能在答案路径中，因为点2连了一条边到点6 ，而点6 不与终点5 连通。

对于30%的数据，0<n≤10，0<m≤20；

对于60%的数据，0<n≤100，0<m≤2000；

对于100%的数据，0<n≤10,000，0<m≤200,000，0<x，y，s，t≤n，x≠t。

反向建图删点

然后spfa

#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int maxn = ;
int head[maxn*];
int ct=,s,t;
int used[maxn],dis[maxn];
int n,m,x[maxn],y[maxn],q[maxn];
struct edge{
    int next;
    int to;
}e[];
void add(int from,int to){
    e[++ct].to=to;
    e[ct].next=head[from];
    head[from]=ct;
    return;
}
bool pd(int pos){
    int i;
    for(i=head[pos];i;i=e[i].next){
        if(!used[e[i].to])return ;//未与终点联通
    }
    return ;
}
void spfa()
{
    memset(head,,sizeof(head));
    memset(q,,sizeof(q));
    memset(dis,-,sizeof(dis));
    ct=;
    for(int i=;i<=m;i++){
        add(x[i],y[i]);
    }
    q[]=s;
    dis[s]=;
    int hd=,tl=;
    int ans=;
    while(hd<=tl){
        int pos=q[hd];hd++;
        if(hd==maxn)hd=;
        if(pd(pos)==)continue;
        for(int i=head[pos];i;i=e[i].next){
            if(dis[e[i].to]==-)
            {
                dis[e[i].to]=dis[pos]+;
                q[tl++]=e[i].to;
                if(tl==maxn)tl=;
                if(e[i].to==t){
                    ans=dis[t];
                    printf("%d\n",ans);
                    return;
                }
            }
        }
    }
    puts("-1");
    return;
}
void work()
{
    int hd=,tl=;
    q[]=t;
    used[t]=;
    while(hd<=tl){
        int pos=q[hd];hd++;
        if(hd==maxn)hd=;
        for(int i=head[pos];i;i=e[i].next){
            if(!used[e[i].to]){
                q[++tl]=e[i].to;
                if(tl==maxn)tl=;
                used[e[i].to]=;
            }
        }
    }
    if(!used[s]){
        puts("-1");
        return;
    }
    else spfa();
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=;i<=m;i++){
        scanf("%d%d",&x[i],&y[i]);
        add(y[i],x[i]);
    }
    scanf("%d%d",&s,&t);
    work();
    return ;
}