Luogu P4287 SHOI2011 双倍回文 题解 [ 紫 ] [ manacher ]

双倍回文：回文子串结论的经典应用。

结论

先放本题最关键的结论：一个字符串本质不同的回文子串最多只有 \(n\) 个。

考虑如何证明：

假设我们一个一个地在当前字符串（黑色部分）的结尾加入字符（红色部分），那么会出现如下情况：

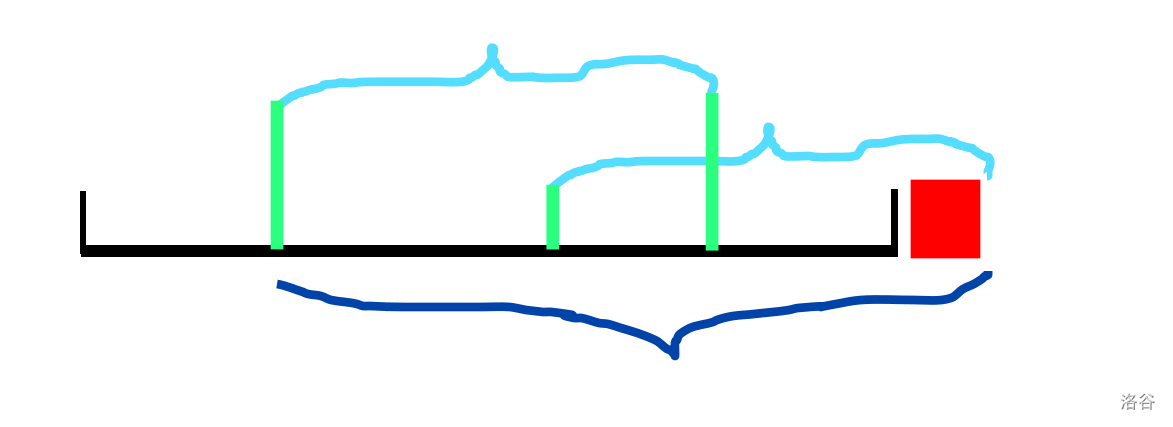
显然，加入红色字符后，字符串中最多只可能新出现一个本质不同的回文子串。如果这个本质不同的回文子串存在，则这个回文子串就是当前最长的回文子串（深蓝色部分）。

为啥呢，因为假设存在一个更短的回文子串（浅蓝色部分），我们称这个浅蓝色的短回文子串为 \(s\)，深蓝色的最长回文子串为 \(t\)，则 \(t\) 中一定包含了 \(s\)。而根据回文串的性质，\(s\) 正着读反着读都相同，因此深蓝色的回文串 \(t\) 另一边一定存在另一个 \(s\)，且那个 \(s\) 的结尾比当前 \(s\) 的结尾靠前（这两个 \(s\) 在图中用浅蓝色划出来了）。因此它已经被计入本质不同的回文子串中了。

思路

有了这个结论，剩下的就简单了，我们只需要对每个本质不同的回文串判断一下就可以了。

用 manacher 来实现，在每次扩展盒子右端点时统计新拓展部分的回文子串，注意特判细节即可。

因为右端点最多只会拓展 \(n\) 次，所以时间复杂度 \(O(n)\)。

代码

#include <bits/stdc++.h>
#define fi first
#define se second
#define lc (p<<1)
#define rc ((p<<1)|1)
#define eb(x) emplace_back(x)
#define pb(x) push_back(x)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef long double ldb;
using pi=pair<int,int>;
int m,n,ans=0,d[1000005];
char a[500005],s[1000005];
void init()
{
    n=0;
    s[0]='$';
    s[++n]='#';
    for(int i=1;i<=m;i++)s[++n]=a[i],s[++n]='#';
    s[n+1]='&';
}
void manacher()
{
    d[1]=1;
    for(int i=2,l=0,r=0;i<=n;i++)
    {
        if(i<=r)d[i]=min(r-i+1,d[l+r-i]);
        while(s[i-d[i]]==s[i+d[i]])d[i]++;
        if(i+d[i]-1>r)
        {
            if(s[i]=='#')
            {
                for(int j=r+1;j<=i+d[i]-1;j++)
                {
                    if(s[j]=='#')continue;
                    int dxx=(j-i+1)/2,c=i-dxx;
                    if(d[c]/2>=dxx/2&&s[c]=='#'&&dxx>=1&&dxx*2%4==0)ans=max(ans,dxx*2);
                }
            }
            l=i-d[i]+1,r=i+d[i]-1;
        }
    }
}
int main()
{
    //freopen("sample.in","r",stdin);
    //freopen("sample.out","w",stdout);
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin>>m>>a+1;
    init();
    manacher();
    cout<<ans;
    return 0;
}