『MXNet』第十一弹_符号式编程初探

一、符号分类

符号对我们想要进行的计算进行了描述, 下图展示了符号如何对计算进行描述.

我们定义了符号变量A, 符号变量B, 生成了符号变量C, 其中, A, B为参数节点, C为内部节点! mxnet.symbol.Variable可以生成参数节点, 用于表示计算时的输入.

二、常用符号方法

一个Symbol具有的属性和方法如下图所示:

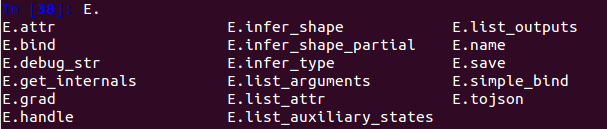
关联节点查看

list_arguments()用来检查计算图的输入参数;

list_outputs()返回此Symbol的所有输出，输出的自动命名遵循一定的规则

input = mx.sym.Variable('data')  # 生成一个符号变量,名字是可以随便取的
fc1 = mx.sym.FullyConnected(data=input, num_hidden=128,name='fc1')  # 全连接层
act1 = mx.sym.Activation(fc1, act_type='relu')  # 激活

type(fc1)  # mxnet.symbol.Symbol, act1的类型也是这个!!!
fc1.list_outputs()  # ['fc1_output'],自动在输入name属性名的后面加上"_output"作为本节点名称
fc1.list_arguments()  # ['data','fc1_weight','fc1_bias'],自动生成fc1_weight,fc1_bias两个参数节点

act1.list_outputs()  # ['actvation0_output'] 这个名字就不是随便起的了!!!
act1.list_arguments()  # ['data','fc1_weight','fc1_bias']

返回逻辑如下图，

数据维度推断

mxnet.symbol.Symbol.infer_shape(self, *args, **kwargs): 推测输入参数和输出参数的shape, 返回一个list of tuple;

a = mx.sym.Variable('A')
b = mx.sym.Variable('B')
c = (a + b) / 10
d = c + 1
input_shapes = {'A':(10,2), 'B':(10,2)}   # 定义输入的shape
d.infer_shape(**input_shapes) # ([(10L, 2L), (10L, 2L)], [(10L, 2L)], [])
arg_shapes, out_shapes, aux_shapes = d.infer_shape(**input_shapes)

In [1]: arg_shapes

Out[1]: [(10L, 2L), (10L, 2L)]

In [2]: out_shapes

Out[2]: [(10L, 2L)]

In [3]: aux_shapes

Out[3]: []

附、可视化

mx.viz.plot_network(d).view()

三、绑定执行

A = mx.sym.Variable('A')
B = mx.sym.Variable('B')
C = A * B
D = mx.sym.Variable('D')
E = C + D
a = mx.nd.empty(1)  # 生成一个维度为1的随机值
b = mx.nd.ones(1)    # b等于1
d = mx.nd.ones(1)
executor = E.bind(ctx=mx.cpu(), args={'A':a, 'B':b, 'D':d})
type(executor)  # mxnet.executor.Executor
executor.arg_dict  # {'A': <NDArray 1 @cpu(0)>, 'B': <NDArray 1 @cpu(0)>, 'D': <NDArray 1 @cpu(0)>}
executor.forward()  # [<NDArray 1 @cpu(0)>]
executor.outputs[0]  # <NDArray 1 @cpu(0)>, 值呢? 还是看不到值啊???
executor.outputs[0].asnumpy()  # array([ 1.], dtype=float32)

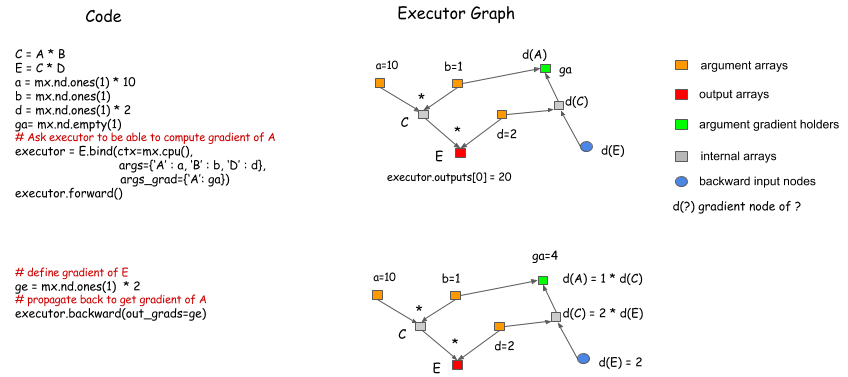
首先我们需要调用绑定函数(bind function:*.bind)来绑定NDArrays(下图中的a/b/d)到参数节点(argument nodes: A/B/D,不是内部节点C/E),从而获得一个执行器(Executor)，其作用是获取数组大小，以分配内存或显存：

然后,调用Executor.Forward 便可以得到输出结果.

执行器属性方法如下：

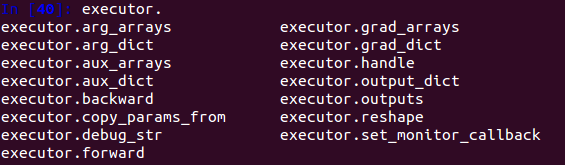
绑定多个输出

我们可以使用mx.symbol.Group([])来将symbols进行分组,然后将它们进行绑定，从而得到更多的中间变量输出。

下图中,A/B/D为参数节点,C/E为内部节点,将E/C绑定为G,这样,E和C的计算结果都可以得到，但是出于优化计算图的考虑，不建议过多绑定输出节点。

梯度计算

在绑定函数中,可以指定NDArrays来保存梯度,在Executor.forward()的后面调用Executor.backward()可以得到相应的梯度值.

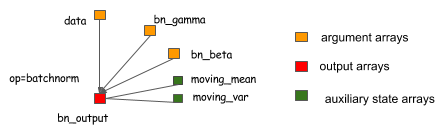
辅助变量

四、新建symbol节点

文档介绍

官方文档例子，复现一个softmax节点，并进行一次反向传播（没有更新参数）：

import mxnet as mx
from mxnet.test_utils import get_mnist_iterator
import numpy as np
import logging
import mxnet.ndarray as nd

class Softmax(mx.operator.CustomOp):
    def forward(self, is_train, req, in_data, out_data, aux):
        x = in_data[0].asnumpy()
        y = np.exp(x - x.max(axis=1).reshape((x.shape[0], 1)))
        y /= y.sum(axis=1).reshape((x.shape[0], 1))
        self.assign(out_data[0], req[0], mx.nd.array(y))

    def backward(self, req, out_grad, in_data, out_data, in_grad, aux):
        l = in_data[1].asnumpy().ravel().astype(np.int)
        y = out_data[0].asnumpy()
        y[np.arange(l.shape[0]), l] -= 1.0
        self.assign(in_grad[0], req[0], mx.nd.array(y))

@mx.operator.register("softmax")
class SoftmaxProp(mx.operator.CustomOpProp):
    def __init__(self):
　　　　"""使用need_top_grad = False调用基础构造函数，
　　　　　 因为softmax是一个损失层，不需要前面层的梯度输入"""
        super(SoftmaxProp, self).__init__(need_top_grad=False)

    def list_arguments(self):
        return ['data', 'label']

    def list_outputs(self):
        return ['output']

    def infer_shape(self, in_shape):
　　　　"""提供infer_shape来声明输出/权重的形状并检查输入形状的一致性"""
        data_shape = in_shape[0]
        label_shape = (in_shape[0][0],)
        output_shape = in_shape[0]
        return [data_shape, label_shape], [output_shape], []

    def infer_type(self, in_type):
        return in_type, [in_type[0]], []

    def create_operator(self, ctx, shapes, dtypes):
　　　　"""定义一个create_operator函数，该函数将由后端调用以创建softmax的实例"""
        return Softmax()
# define mlp

net = mx.sym.Variable('data')
net = mx.sym.FullyConnected(net, name='fc', num_hidden=6)
net = mx.sym.Activation(net, name='relu', act_type="relu")
mlp = mx.symbol.Custom(data=net, name='softmax', op_type='softmax')

# train
# logging.basicConfig(level=logging.DEBUG)
logging.basicConfig(level=logging.INFO)

# MXNET_CPU_WORKER_NTHREADS must be greater than 1 for custom op to work on CPU
context=mx.cpu()
# Uncomment this line to train on GPU
# context=mx.gpu(0)
print(mlp.list_arguments(), mlp.list_outputs())
input_shapes = {'data':(5, 28*28)}
print(mlp.infer_shape(**input_shapes))

args =  {'data': mx.nd.ones((1, 4)), 'fc_weight': mx.nd.ones((6, 4)),
         'fc_bias': mx.nd.array((1, 4, 4, 4, 5, 6)), 'softmax_label': mx.nd.ones((1))}
args_grad = {'fc_weight': mx.nd.zeros((6, 4)), 'fc_bias': mx.nd.zeros((6))}

executor = mlp.bind(ctx=mx.cpu(0), args=args, args_grad=args_grad, grad_req='write')

# 所有参数节点数组
print("executor.arg_dict 初始值\n", executor.arg_dict)

# 所有参数节点对应梯度数组
print("executor.grad_dict 初始值\n", executor.grad_dict)

executor.backward()

# # data
# train, val = get_mnist_iterator(batch_size=100, input_shape = (784,))
# mod = mx.mod.Module(mlp, context=context)
# mod.fit(train_data=train, eval_data=val, optimizer='sgd',
#     optimizer_params={'learning_rate':0.1, 'momentum': 0.9, 'wd': 0.00001},
#     num_epoch=10, batch_end_callback=mx.callback.Speedometer(100, 100))

['data', 'fc_weight', 'fc_bias', 'softmax_label'] ['softmax_output']
([(5, 784), (6, 784), (6,), (5,)], [(5, 6)], [])
executor.arg_dict 初始值
 {'data':
[[1. 1. 1. 1.]]
<NDArray 1x4 @cpu(0)>, 'fc_weight':
[[1. 1. 1. 1.]
 [1. 1. 1. 1.]
 [1. 1. 1. 1.]
 [1. 1. 1. 1.]
 [1. 1. 1. 1.]
 [1. 1. 1. 1.]]
<NDArray 6x4 @cpu(0)>, 'fc_bias':
[1. 4. 4. 4. 5. 6.]
<NDArray 6 @cpu(0)>, 'softmax_label':
[1.]
<NDArray 1 @cpu(0)>}
executor.grad_dict 初始值
 {'data': None, 'fc_weight':
[[0. 0. 0. 0.]
 [0. 0. 0. 0.]
 [0. 0. 0. 0.]
 [0. 0. 0. 0.]
 [0. 0. 0. 0.]
 [0. 0. 0. 0.]]
<NDArray 6x4 @cpu(0)>, 'fc_bias':
[0. 0. 0. 0. 0. 0.]
<NDArray 6 @cpu(0)>, 'softmax_label': None}

可以看到，bind方法其实蛮麻烦的，需要将参数、梯度参数全部初始化，才能进行下一步的操作，这就引出了两个其他方法：

• 仅仅指定输入shape以申请内存的Symbol.simple_bind()，其参数仅仅是shape，这也意味这此方法仅仅能够测试，由于没有引进实际数据执行forward、backward两个方法的返回值并无意义。
• mxnet.mod.Module类，集成了参数初始化、前传反传、参数更新等一系列方法，简化了训练的繁琐，个人感觉是介于gluon和基础symbol之间产物。

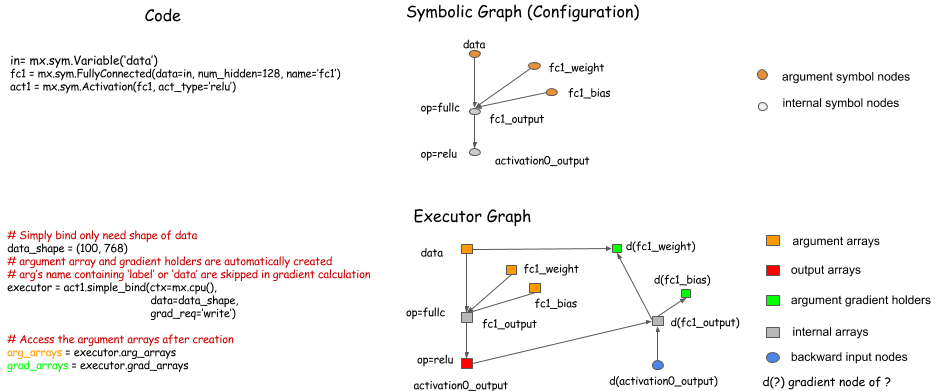
simple_bind

反向传播时，我们需要定义很多新的grad节点并绑定给Executor，过程较为繁琐，Symbol.simple_bind()函数可以帮助我们简化这个过程,指定输入数据的大小(shape),这个函数可以定位梯度参数并将其绑定为Executor.

v1 = mx.ndarray.array([[1, 1]])
v2 = mx.ndarray.array([[2, 2]])
v3 = mx.ndarray.array([[3, 3]])
a = mx.symbol.Variable('a')
b = mx.symbol.Variable('b')
c = mx.symbol.Variable('c')
d = b + c
b_stop_grad = mx.symbol.BlockGrad(3 * d)
loss = mx.sym.MakeLoss(b_stop_grad + a)
executor = loss.simple_bind(ctx=mx.cpu(), a=(1,2), b=(1,2), c=(1,2))
executor.forward(is_train=True, a=v1, b=v2, c=v3)
executor.outputs
Out[5]: 
[
 [[16. 16.]]
 <NDArray 1x2 @cpu(0)>]
executor.backward()
executor.grad_dict
Out[6]: 
{'b': 
 [[0. 0.]]
 <NDArray 1x2 @cpu(0)>, 'c': 
 [[0. 0.]]
 <NDArray 1x2 @cpu(0)>, 'a': 
 [[1. 1.]]
 <NDArray 1x2 @cpu(0)>}

五、Modue对象

更为常用的方法是使用symbol生成计算图后将之转换为Module对象，再进行训练，

import mxnet as mx

# construct a simple MLP
data = mx.symbol.Variable('data')
fc1  = mx.symbol.FullyConnected(data, name='fc1', num_hidden=128)
act1 = mx.symbol.Activation(fc1, name='relu1', act_type="relu")
fc2  = mx.symbol.FullyConnected(act1, name = 'fc2', num_hidden = 64)
act2 = mx.symbol.Activation(fc2, name='relu2', act_type="relu")
fc3  = mx.symbol.FullyConnected(act2, name='fc3', num_hidden=10)
out  = mx.symbol.SoftmaxOutput(fc3, name = 'softmax')

# construct the module
mod = mx.mod.Module(out)

mod.bind(data_shapes=train_dataiter.provide_data,
    label_shapes=train_dataiter.provide_label)

mod.init_params()
mod.fit(train_dataiter, eval_data=eval_dataiter,
       optimizer_params={'learning_rate':0.01, 'momentum': 0.9},
       num_epoch=n_epoch

首先是定义了一个简单的MLP，symbol的名字就叫做out，然后可以直接用mx.mod.Module来创建一个mod。之后mod.bind的操作是在显卡上分配所需的显存，所以我们需要把data_shapehe label_shape传递给他，然后初始化网络的参数，再然后就是mod.fit开始训练了。

fit方法核心代码如下：

for epoch in range(begin_epoch, num_epoch):
     tic = time.time()
     eval_metric.reset()
     for nbatch, data_batch in enumerate(train_data):
         if monitor is not None:
             monitor.tic()
         self.forward_backward(data_batch) #网络进行一次前向传播和后向传播
         self.update()  #更新参数
         self.update_metric(eval_metric, data_batch.label) #更新metric

         if monitor is not None:
             monitor.toc_print()

         if batch_end_callback is not None:
             batch_end_params = BatchEndParam(epoch=epoch, nbatch=nbatch,
                                              eval_metric=eval_metric,
                                              locals=locals())
             for callback in _as_list(batch_end_callback):
                 callback(batch_end_params)

对于训练过程我们可以做出很多改进，举个最简单的例子：如果我们的训练网络是大小可变怎么办？ 我们可以实现一个mutumodule，基本上就是，每次data的shape变了的时候，我们就重新bind一下symbol，这样训练就可以照常进行了。