数据结构(Splay平衡树)：HDU 1890 Robotic Sort

Robotic Sort

Time Limit: 6000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 3456    Accepted Submission(s): 1493

Problem Description

　　Somewhere
deep in the Czech Technical University buildings, there are
laboratories for examining mechanical and electrical properties of
various materials. In one of yesterday’s presentations, you have seen
how was one of the laboratories changed into a new multimedia lab. But
there are still others, serving to their original purposes.

　　In
this task, you are to write software for a robot that handles samples in
such a laboratory. Imagine there are material samples lined up on a
running belt. The samples have different heights, which may cause
troubles to the next processing unit. To eliminate such troubles, we
need to sort the samples by their height into the ascending order.

　　Reordering
is done by a mechanical robot arm, which is able to pick up any number
of consecutive samples and turn them round, such that their mutual order
is reversed. In other words, one robot operation can reverse the order
of samples on positions between A and B.

　　A possible way to sort
the samples is to find the position of the smallest one (P1) and reverse
the order between positions 1 and P1, which causes the smallest sample
to become first. Then we find the second one on position P and reverse
the order between 2 and P2. Then the third sample is located etc.

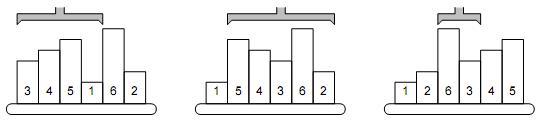
　　The
picture shows a simple example of 6 samples. The smallest one is on the
4th position, therefore, the robot arm reverses the first 4 samples.
The second smallest sample is the last one, so the next robot operation
will reverse the order of five samples on positions 2–6. The third step
will be to reverse the samples 3–4, etc.

　　Your task is to find
the correct sequence of reversal operations that will sort the samples
using the above algorithm. If there are more samples with the same
height, their mutual order must be preserved: the one that was given
first in the initial order must be placed before the others in the final
order too.

 

Input

　　The
input consists of several scenarios. Each scenario is described by two
lines. The first line contains one integer number N , the number of
samples, 1 ≤ N ≤ 100 000. The second line lists exactly N
space-separated positive integers, they specify the heights of
individual samples and their initial order.

The last scenario is followed by a line containing zero.

 

Output

　　For each scenario, output one line with exactly N integers P1 , P1 , . . . PN ,separated by a space.
Each Pi must be an integer (1 ≤ Pi ≤ N ) giving the position of the i-th sample just before the i-th reversal operation.

　　Note
that if a sample is already on its correct position Pi , you should
output the number Pi anyway, indicating that the “interval between Pi
and Pi ” (a single sample) should be reversed.

 

Sample Input

　　6
3 4 5 1 6 2
4
3 3 2 1
0

 

Sample Output

　　4 6 4 5 6 6
4 2 4 4

 

　　这道题很简单，注意Push_down就好了。

 #include <algorithm>
 #include <iostream>
 #include <cstring>
 #include <cstdio>
 using namespace std;
 const int maxn=;
 int n,fa[maxn],ch[maxn][],sz[maxn];
 int flip[maxn],pos[maxn],rt;
 struct Node{
     int x,id;
 }a[maxn];

 void Flip(int x){
     swap(ch[x][],ch[x][]);
     flip[x]^=;
 }

 void Push_down(int x){
     if(flip[x]){
         Flip(ch[x][]);
         Flip(ch[x][]);
         flip[x]=;
     }
 }

 int pd[maxn];
 void P(int x){
     int cnt=;
     while(x){
         pd[++cnt]=x;
         x=fa[x];
     }
     while(cnt){
         Push_down(pd[cnt--]);
     }
 }

 void Push_up(int x){
     sz[x]=sz[ch[x][]]+sz[ch[x][]]+;
 }

 void Rotate(int x){
     int y=fa[x],g=fa[y],c=ch[y][]==x;
     ch[y][c]=ch[x][c^];fa[ch[x][c^]]=y;
     ch[x][c^]=y;fa[y]=x;fa[x]=g;
     if(g)ch[g][ch[g][]==y]=x;
     Push_up(y);
 }

 void Splay(int x,int g=){
     P(x);
     for(int y;(y=fa[x])!=g;Rotate(x))
         if(fa[y]!=g)
             Rotate((ch[fa[y]][]==y)==(ch[y][]==x)?y:x);
     Push_up(x);
     if(!g)rt=x;
 }

 int Build(int f,int l,int r){
     if(l>r)return ;
     int mid=(l+r)>>;fa[mid]=f;
     ch[mid][]=Build(mid,l,mid-);
     ch[mid][]=Build(mid,mid+,r);
     sz[mid]=;
     Push_up(mid);
     return mid;
 }

 bool cmp(Node a,Node b){
     if(a.x!=b.x)
     return a.x<b.x;
     return a.id<b.id;
 }

 int main(){
     while(~scanf("%d",&n)&&n){
         memset(flip,,sizeof(flip));
         rt=Build(,,n+);
         for(int i=;i<=n;i++)
             scanf("%d",&a[i].x);
         for(int i=;i<=n;i++)
             a[i].id=i;
         sort(a+,a+n+,cmp);
         for(int i=;i<=n;i++)
             pos[i+]=a[i].id+;
         pos[]=;pos[n+]=n+;
         for(int i=,p;i<n+;i++){
             Splay(pos[]);
             Splay(pos[i],pos[]);
             printf("%d ",sz[ch[ch[rt][]][]]+);
             Splay(pos[i]);
             p=ch[pos[i]][];
             while(ch[p][]){
                 Push_down(p);
                 p=ch[p][];
             }
             Push_down(p);
             Splay(pos[i-]);
             Splay(p,pos[i-]);
             Flip(ch[ch[rt][]][]);
         }
         printf("%d\n",n);
     }
     return ;
 }