[CTSC2008]祭祀

题目描述

　　在遥远的东方，有一个神秘的民族，自称Y族。他们世代居住在水面上，奉龙王为神。每逢重大庆典， Y族都会在水面上举办盛大的祭祀活动。我们可以把Y族居住地水系看成一个由岔口和河道组成的网络。每条河道连接着两个岔口，并且水在河道内按照一个固定的方向流动。显然，水系中不会有环流（下图描述一个环流的例子）。

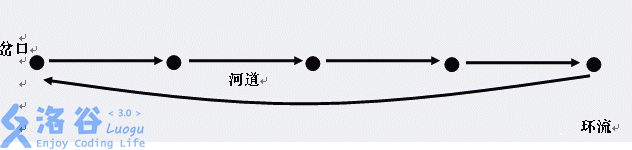
　　由于人数众多的原因，Y族的祭祀活动会在多个岔口上同时举行。出于对龙王的尊重，这些祭祀地点的选择必须非常慎重。准确地说，Y族人认为，如果水流可以从一个祭祀点流到另外一个祭祀点，那么祭祀就会失去它神圣的意义。族长希望在保持祭祀神圣性的基础上，选择尽可能多的祭祀的地点。

输入输出格式

输入格式：

第一行包含两个用空格隔开的整数N、M，分别表示岔口和河道的数目，岔口从1到N编号。

接下来M行，每行包含两个用空格隔开的整数u、v，描述一条连接岔口u和岔口v的河道，水流方向为自u向v。

输出格式：

　第一行包含一个整数K，表示最多能选取的祭祀点的个数。 接下来一行输出一种可行的选取方案。对于每个岔口依次输出一个整数，如果在该岔口设置了祭祀点，那么输出一个1，否则输出一个0。应确保你输出的1 的个数最多，且中间没有空格。 接下来一行输出，在选择最多祭祀点的前提下，每个岔口是否能够设置祭祀点。对于每个岔口依次输出一个整数，如果在该岔口能够设置祭祀点，那么输出一个 1，否则输出一个0。 注意：多余的空格和换行可能会导致你的答案被判断为错误答案。

输入输出样例

输入样例#1： 复制

4 4
1 2
3 4
3 2
4 2

输出样例#1： 复制

2
1010
1011

说明

N ≤ 100 M ≤ 1 000

在样例给出的水系中，不存在一种方法能够选择三个或者三个以上的祭祀点。包含两个祭祀点的测试点的方案有两种：

选择岔口1与岔口3（如样例输出第二行），选择岔口1与岔口4。

水流可以从任意岔口流至岔口2。如果在岔口2建立祭祀点，那么任意其他岔口都不能建立祭祀点但是在最优的一种祭祀点的选取方案中我们可以建立两个祭祀点，所以岔口2不能建立祭祀点。对于其他岔口至少存在一个最优方案选择该岔口为祭祀点，所以输出为1011。

没有spj，不用输出后面那些的，只要输出最大值就可以了

这题涉及

最长反链与最小链覆盖

这就是传说中的Dilworth定理：最小链覆盖数 = 最长反链长度。

其对偶定理：最长链长度 = 最小反链覆盖数

然后用二分图匹配，求出最大匹配

最小链覆盖即为n-最大匹配

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<cmath>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 struct Node
 {
   int next,to;
 }edge[];
 int n,m,head[],match[],vis[],num,map[][],ans;
 void add(int u,int v)
 {
   num++;
   edge[num].next=head[u];
   head[u]=num;
   edge[num].to=v;
 }
 bool dfs(int x)
 {int i;
   for (i=head[x];i;i=edge[i].next)
     {
       int v=edge[i].to;
       if (vis[v]) continue;
       vis[v]=;
       if (match[v]==-||dfs(match[v]))
     {
       match[v]=x;
       return ;
     }
     }
   return ;
 }
 int main()
 {int i,j,u,v,k;
   cin>>n>>m;
   for (i=;i<=m;i++)
     {
       scanf("%d%d",&u,&v);
       map[u][v]=;
     }
   for (k=;k<=n;k++)
     for (i=;i<=n;i++)
       for (j=;j<=n;j++)
     map[i][j]|=map[i][k]&map[k][j];
   for (i=;i<=n;i++)
     for (j=;j<=n;j++)
       if (map[i][j]) add(i,n+j),add(n+j,i);
   memset(match,-,sizeof(match));
   for (i=;i<=n;i++)
     {
       memset(vis,,sizeof(vis));
       if (dfs(i)) ans++;
     }
   cout<<n-ans;
 }