C# 高斯消元项目运用

最近项目涉及到一个需求，需要把指定数量的多个商品，混合装入到多个不同型号的箱子中(每种型号的箱子装入商品的种类和个数是固定的)。这就涉及到解多元一次方程

  • 针对多元一次方程一般用高斯消元去处理，当消元后仍有不能消掉的元 则需要解多元一次方程

1. 将数据转换为二维数组，消元代码如下

  • 样本数据如下
    ***
    | 2, 3, 4, 3, 21 | => | 2, 3, 4, 3, 21 | => | 2, 3, 4, 3 , 21 |

    | 3, 1, 6, 2, 17 | => | 0, 7, 0, 5, 29 | => | 0, 7, 0, 5 , 29 |

    | 1, 3, 2, 1, 12 | => | 0, -3,0, 1, -3 | => | 0, 0, 0, -22, -66 |

    ***

               var rowLength = arr.GetLength(0);//行数
                var colLength = arr.GetLength(1);//列数

                for (int mainCol = 0; mainCol < colLength - 1; mainCol++) //按照列，一列一列的消元
                {
                    var mainRow = mainCol; //主元行=主元列

                    for (int row = mainRow + 1; row < rowLength; row++) // 从主元的下一行开始 行循环
                    {
                        if (row >= (colLength - 1))
                            break;
                        /
                            n1    X + n2Y = a   
                            m1    X + m2Y = b  
                            =>  n1    m1X + n2m1Y = am1
                            =>  m1    n1X + m2n1Y = bn1
                        /
                        //如果主元参数为0（ 找出此列不为0的行） 运用行相加  变换0参数
                        if (arr[mainRow, mainCol] == 0)
                        {
                            for (int rowi = mainRow + 1; rowi < rowLength; rowi++)
                            {
                                if (arr[rowi, mainCol] != 0)
                                {
                                    for (int colj = mainCol; colj < colLength; colj++)
                                    {
                                        arr[mainRow, colj] += arr[rowi, colj];
                                    }
                                    break;
                                }
                            }
                        }

                        if (arr[row, mainCol] == 0)
                            continue; //当前行 此列已经是0 继续消元下一行

                        var m = GetMinCommonMultiple(arr[mainCol, mainCol], arr[row, mainCol]);

                        int factorMain = m / arr[mainCol, mainCol];//主列的因子  
                        int factor = m / arr[row, mainCol]; //待消元列因子

                        for (int colk = mainCol; colk < colLength; colk++)
                        {
                            arr[row, colk] = arr[mainCol, colk]      factorMain - arr[row, colk] * factor;
                        }
                    }
                }

2. 消元后，找出仍然无法消除的元，解一元多次不定方程

  • 通过消元 最终可以确定 a[3]=3 ,a[1]=2 a[0]和a[2]解有多个 需要解不定方程思路是将 多元方程切割成二元方程然后穷举求解。 列入3x+2y+4z+6a=18, 令 w=2y+4z+6a,再令 2w=2(y+2z+3a) ,带入公式 得 3x+2w=16,穷举求出一个解 x=2 w=6 ，然后 再解 y+2z+3a=6。 同样的方法再次处理
  • 代码如下
          /// <summary>
            /// 解不定方程
            /// </summary>
            public static bool ResoveIndefiniteEquation(int[] arr, int value, int startIndex, ref int[] result, ref int count)
            {
                count++;//递归计数，防止无限递归

                if (arr == null || arr.Length == 0)
                    return false;

                if (arr.Length == 1)
                {
                    var reValue = value / arr[0];
                    if (value % arr[0] == 0 && reValue >= MinResove && reValue <= MaxResove)
                    {
                        result[startIndex] = reValue;
                        return true;
                    }
                    return false;
                }

                //获取第二部分元的最大公约数
                var commonDivisor = arr[1];
                for (int i = 1; i < (arr.Length - 1); i++)
                {
                    commonDivisor = GetCommonDivisor(commonDivisor, arr[i + 1]);
                }

                for (int i = MinResove; i <= MaxResove; i++)
                {
                    var currValue = value - i * arr[0];
                    if (currValue % commonDivisor == 0)
                    {
                        var newArr = new int[arr.Length - 1];
                        Array.Copy(arr, 1, newArr, 0, arr.Length - 1);

                        result[startIndex] = i;
                        var currArr = ResoveIndefiniteEquation(newArr, currValue, startIndex + 1, ref result, ref count);
                        if (currArr)
                            return true;

                        if (count > 1000000)
                        {
                            Console.WriteLine("递归太深无法求解");
                            return false;
                        }
                    }
                }
                return false;
            }

3.完整代码

    public class GaussHelper
    {
        /// <summary>
        /// 不定方程解的最小值
        /// </summary>
        private const int MinResove = 1;

/// <summary>
        /// 不定方程解的最大值
        /// </summary>

private const int MaxResove = 100;

/// <summary>
        /// 利用高斯消元求解一元多次方程组
        /// </summary>
        /// <param name="arr"></param>
        public static int?[] ResoveGauss(int[,] arr)
        {
            if (arr == null) throw new ArgumentNullException("arr");

var rowLength = arr.GetLength(0);//行数
            var colLength = arr.GetLength(1);//列数

if (colLength < 2) throw new IndexOutOfRangeException("arr.GetLength(1)的值必须大于等于2");

var result = new int?[colLength - 1];
#if DEBUG
            Console.WriteLine("解一元多次方程：");
            PrintArr(arr);
#endif

for (int mainCol = 0; mainCol < colLength - 1; mainCol++) //按照列，一列一列的消元
            {
                var mainRow = mainCol; //主元行=主元列

for (int row = mainRow + 1; row < rowLength; row++) // 从主元的下一行开始 行循环
                {
                    if (row >= (colLength - 1))
                        break;
                    /*
                        n1*X + n2*Y = a   
                        m1*X + m2*Y = b  
                        =>  n1*m1*X + n2*m1Y = a*m1
                        =>  m1*n1*X + m2*n1*Y = b*n1
                    */
                    //如果主元参数为0（ 找出此列不为0的行） 运用行相加  变换0参数
                    if (arr[mainRow, mainCol] == 0)
                    {
                        for (int rowi = mainRow + 1; rowi < rowLength; rowi++)
                        {
                            if (arr[rowi, mainCol] != 0)
                            {
                                for (int colj = mainCol; colj < colLength; colj++)
                                {
                                    arr[mainRow, colj] += arr[rowi, colj];
                                }
                                break;
                            }
                        }
                    }

if (arr[row, mainCol] == 0)
                        continue; //当前行 此列已经是0 继续消元下一行

var m = GetMinCommonMultiple(arr[mainCol, mainCol], arr[row, mainCol]);

int factorMain = m / arr[mainCol, mainCol];//主列的因子  
                    int factor = m / arr[row, mainCol]; //待消元列因子

for (int colk = mainCol; colk < colLength; colk++)
                    {
                        arr[row, colk] = arr[mainCol, colk] * factorMain - arr[row, colk] * factor;
                    }
                }
#if DEBUG
                if (rowLength > mainCol + 1)
                    PrintArr(arr);
#endif
            }

//回代过程 
            //回代行 判断 行数是否大于列数减-1  取到可以计算结果的回代行
            var backRow = rowLength > (colLength - 1) ? colLength - 1 : rowLength;
            var backRowIndex = backRow - 1;

//回代行的结果值
            var backValue = arr[backRowIndex, colLength - 1];

//判断消解行 有多少个变元 ，存储 变元的 索引
            var listColIndex = new List<int>();
            for (int col = 0; col < colLength - 1; col++)
            {
                if (arr[backRowIndex, col] != 0)
                {
                    listColIndex.Add(col);
                }
            }

if (listColIndex.Count == 0)
                return null;

//根据需要求解的个数 解不定方程处理

if (listColIndex.Count > 1)
            {
                var resoveArr = listColIndex.Select(x => arr[backRowIndex, x]).ToArray();
                var resoveResultArr = new int[listColIndex.Count];
                var count = 0;
                var flag = ResoveIndefiniteEquation(resoveArr, backValue, 0, ref resoveResultArr, ref count);
#if DEBUG
                Console.WriteLine();
                Console.WriteLine("--解不定方程");
                var sb = new StringBuilder();
                for (int i = 0; i < colLength; i++)
                {
                    sb.Append("********");
                }
                Console.WriteLine(sb.ToString());

Console.WriteLine($"方程: {string.Join(",\t", resoveArr)} = {backValue}");
                Console.WriteLine($"结果: {string.Join(",\t", resoveResultArr)}");
                Console.WriteLine($"计算: {string.Join(",\t", resoveResultArr.Select((x, index) => $"{x * resoveArr[index]}"))}");
                Console.WriteLine($"递归次数: {count}");
                Console.WriteLine(sb.ToString());
                Console.WriteLine();
#endif
                if (!flag)
                    return null;

for (int i = 0; i < resoveResultArr.Length; i++)
                {
                    result[listColIndex[i]] = resoveResultArr[i];
                }
            }

if (listColIndex.Count == 1)
            {
                if (backValue % arr[backRowIndex, listColIndex[0]] == 0)
                {
                    result[listColIndex[0]] = backValue / arr[backRowIndex, listColIndex[0]];
                }
                else
                {
#if DEBUG
                    var number = backValue * 1.0 / arr[backRowIndex, listColIndex[0]];
                    Console.WriteLine($"第{backRow}行 {backValue}/{arr[backRowIndex, listColIndex[0]]} = {number}, 不能被被整除计算失败");
#endif
                    return null;
                }
            }

for (int row = backRowIndex - 1; row >= 0; row--) //从倒数第二行开始往前迭代
            {
                if (arr[row, row] == 0)
                    continue;

int addResult = 0;
                var currlist = new List<int>();
                for (int j = row; j < colLength - 2; j++)//j=2   j 最大值为2，每行未知数可能不止一个，故需要遍历已知的未知数并代入
                {
                    if (!result[j + 1].HasValue && arr[row, j + 1] != 0)
                        currlist.Add(j + 1);//把没有计算出结果的列的索引存入
                    else
                        addResult += result[j + 1].GetValueOrDefault() * arr[row, j + 1];//k代表计算的行，j+1代表的列，系数与解要对应，故都为 j+1
                }

var calculateValue = arr[row, colLength - 1] - addResult;

//发现没有计算出结果的列 解不定方程
                if (currlist.Count > 0)
                {
                    currlist.Add(row);
                    var resoveArr = currlist.Select(x => arr[row, x]).ToArray();
                    var resoveResultArr = new int[currlist.Count];

var count = 0;
                    var flag = ResoveIndefiniteEquation(resoveArr, calculateValue, 0, ref resoveResultArr, ref count);
#if DEBUG
                    Console.WriteLine();
                    Console.WriteLine($"----发现第{row + 1}行 第({string.Join(",", currlist)})列 没有计算出结果，需要解不定方程");
                    var sb = new StringBuilder();
                    for (int i = 0; i < colLength; i++)
                    {
                        sb.Append("********");
                    }
                    Console.WriteLine(sb.ToString());

Console.WriteLine($"方程: {string.Join(",\t", resoveArr)} = {calculateValue}");
                    Console.WriteLine($"结果: {string.Join(",\t", resoveResultArr)}");
                    Console.WriteLine($"计算: {string.Join(",\t", resoveResultArr.Select((x, index) => $"{x * resoveArr[index]}"))}");
                    Console.WriteLine($"递归次数: {count}");
                    Console.WriteLine(sb.ToString());
                    Console.WriteLine();
#endif
                    if (!flag)
                        return null;

for (int i = 0; i < resoveResultArr.Length; i++)
                    {
                        result[currlist[i]] = resoveResultArr[i];
                    }
                }
                else
                {
                    if (calculateValue % arr[row, row] == 0)
                    {
                        result[row] = calculateValue / arr[row, row];//本行的未知数用本行最右边数-本行已知未知数代入系数之差 再除以本未知数系数
                    }
                    else
                    {
#if DEBUG
                        var number = calculateValue * 1.0 / arr[row, row];
                        Console.WriteLine($"第{row + 1}行 {calculateValue}/{arr[row, row]} = {number}, 不能被被整除计算失败");
#endif
                        return null;
                    }
                }
            }

#if DEBUG
            Console.WriteLine("----------结果------------");
            Console.Write($"结果: {string.Join(",", result)}");
#endif
            return result;
        }

/// <summary>
        /// 解不定方程
        /// </summary>
        public static bool ResoveIndefiniteEquation(int[] arr, int value, int startIndex, ref int[] result, ref int count)
        {
            count++;//递归计数，防止无限递归

if (arr == null || arr.Length == 0)
                return false;

if (arr.Length == 1)
            {
                var reValue = value / arr[0];
                if (value % arr[0] == 0 && reValue >= MinResove && reValue <= MaxResove)
                {
                    result[startIndex] = reValue;
                    return true;
                }
                return false;
            }

//获取第二部分元的最大公约数
            var commonDivisor = arr[1];
            for (int i = 1; i < (arr.Length - 1); i++)
            {
                commonDivisor = GetCommonDivisor(commonDivisor, arr[i + 1]);
            }

for (int i = MinResove; i <= MaxResove; i++)
            {
                var currValue = value - i * arr[0];
                if (currValue % commonDivisor == 0)
                {
                    var newArr = new int[arr.Length - 1];
                    Array.Copy(arr, 1, newArr, 0, arr.Length - 1);

result[startIndex] = i;
                    var currArr = ResoveIndefiniteEquation(newArr, currValue, startIndex + 1, ref result, ref count);
                    if (currArr)
                        return true;

if (count > 1000000)
                    {
                        Console.WriteLine("递归太深无法求解");
                        return false;
                    }
                }
            }
            return false;
        }

private static void PrintArr(int[,] arr)
        {
            var rowLength = arr.GetLength(0);//行数
            var colLength = arr.GetLength(1);//列数

var sb = new StringBuilder();
            for (int i = 0; i < colLength; i++)
            {
                sb.Append("--------");
            }
            Console.WriteLine(sb.ToString());
            for (int i = 0; i < rowLength; i++)
            {
                for (int j = 0; j < colLength; j++)
                {
                    Console.Write(arr[i, j]);
                    var str = j == (colLength - 1) ? "" : ",";
                    Console.Write($" {str}\t ");
                }
                Console.WriteLine();
            }
        }

/// <summary>
        /// 求最大公约数
        /// </summary>
        /// <param name="a"></param>
        /// <param name="b"></param>
        /// <returns></returns>
        public static int GetCommonDivisor(int a, int b)
        {
            if (a == 0 || b == 0) return 0;
            if (Math.Abs(a) < Math.Abs(b))
            {
                var temp = a;
                a = b;
                b = temp;
            }
            return (a % b == 0) ? b : GetCommonDivisor(a % b, b);
        }

/// <summary>
        /// 求最小公倍数 
        /// </summary>
        /// <param name="a"></param>
        /// <param name="b"></param>
        /// <returns></returns>
        public static int GetMinCommonMultiple(int a, int b)
        {
            var commonDivisor = GetCommonDivisor(a, b);
            if (commonDivisor == 0)
                return 0;
            return a * b / commonDivisor;
        }
    }

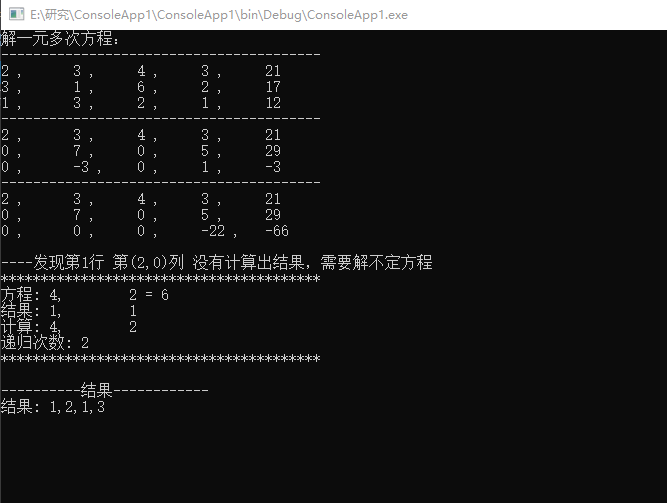
4. 运行结果

        static void Main(string[] args)
        {
            var arr = new int[,]
            {
                { 2, 3, 4, 3, 21 },
                { 3, 1, 6, 2, 17 },
                { 1, 3, 2, 1, 12},
            };
            GaussHelper.ResoveGauss(arr);

Console.ReadKey();
        }

C# 高斯消元项目运用的更多相关文章

  1. 【BZOJ-3143】游走 高斯消元 + 概率期望

    3143: [Hnoi2013]游走 Time Limit: 10 Sec  Memory Limit: 128 MBSubmit: 2264  Solved: 987[Submit][Status] ...

  2. 【BZOJ-3270】博物馆 高斯消元 + 概率期望

    3270: 博物馆 Time Limit: 30 Sec  Memory Limit: 128 MBSubmit: 292  Solved: 158[Submit][Status][Discuss] ...

  3. *POJ 1222 高斯消元

    EXTENDED LIGHTS OUT Time Limit: 1000MS   Memory Limit: 10000K Total Submissions: 9612   Accepted: 62 ...

  4. [bzoj1013][JSOI2008][球形空间产生器sphere] (高斯消元)

    Description 有一个球形空间产生器能够在n维空间中产生一个坚硬的球体.现在,你被困在了这个n维球体中,你只知道球 面上n+1个点的坐标,你需要以最快的速度确定这个n维球体的球心坐标,以便于摧 ...

  5. hihoCoder 1196 高斯消元·二

    Description 一个黑白网格,点一次会改变这个以及与其连通的其他方格的颜色,求最少点击次数使得所有全部变成黑色. Sol 高斯消元解异或方程组. 先建立一个方程组. \(x_i\) 表示这个点 ...

  6. BZOJ 2844 albus就是要第一个出场 ——高斯消元 线性基

    [题目分析] 高斯消元求线性基. 题目本身不难,但是两种维护线性基的方法引起了我的思考. void gauss(){ k=n; F(i,1,n){ F(j,i+1,n) if (a[j]>a[i ...

  7. SPOJ HIGH Highways ——Matrix-Tree定理 高斯消元

    [题目分析] Matrix-Tree定理+高斯消元 求矩阵行列式的值,就可以得到生成树的个数. 至于证明,可以去看Vflea King(炸树狂魔)的博客 [代码] #include <cmath ...

  8. UVALive 7138 The Matrix Revolutions（Matrix-Tree + 高斯消元）（2014 Asia Shanghai Regional Contest）

    题目链接:https://icpcarchive.ecs.baylor.edu/index.php?option=com_onlinejudge&Itemid=8&category=6 ...

  9. [高斯消元] POJ 2345 Central heating

    Central heating Time Limit: 1000MS   Memory Limit: 65536K Total Submissions: 614   Accepted: 286 Des ...

随机推荐

  1. WIN10运行软件，窗口不显示（移动到屏幕外无法复原）的解决办法 Lebal:bug10解决方案

    双显示器切换回单显示器的时候,可能会遇到窗口移动到屏幕外不显示的情况 像这样虽然有缩略图但是点击无反应,并且平铺窗口也不管用,这个时候单击该窗口,Alt+space 执行最小化以及最大化操作即可复原

  2. 求n对括号的合法组合

    一道经典的面试题,求n对括号有多少种合法的组合. 抽象为2n个位置,每个位置可以有2种取值,总共有2^2n个组合,附加约束条件是要符合括号的语法,用来剪枝. 括号语法的合法性条件: 初始化左括号和右括 ...

  3. Linux学习笔记 -- Shell 变量

    定义变量 语法: 变量名=值 myVal= 需要注意一下变量明德规则: 首个字符必须为字母(a-z,A-Z). 中间不能有空格,可以使用下划线(_). 不能使用标点符号. 不能使用bash里的关键字( ...

  4. MariaDB 脚本

    研究MariaDB, 需要mock up一些假数据: 生成n个长度整型数的函数rand_num: CREATE DEFINER=`root`@`localhost` FUNCTION `rand_nu ...

  5. 第八章 数据库连接JDBC（待续）

    ············

  6. leetcode583

    public class Solution { public int MinDistance(string word1, string word2) { , word2.Length + ]; ; i ...

  7. Mybatis工具Generator

    转自:http://www.cuiyongzhi.com/post/36.html MyBatis Generator(以下简称为MBG),可以逆向生成持久层的基本代码,而且mybatis的实现方案比 ...

  8. [原创]JMeter初次使用总结

    引言 最近开发 java 后端项目,对外提供Restful API接口,完整功能开发现已完成. 目前通过单测(68%行覆盖率)已保证业务逻辑正确性,同时也尝试使用JMeter进行压力测试以保证并发性能 ...

  9. linux进程的管道通信

    linux进程的管道通信 要求 编程实现进程的管道通信,掌握管道通信的同步和互斥机制. 相关函数 pipe管道 指用于连接一个读进程和一个写进程以实现他们之间通信的一个共享文件,又名pipe文件.向管 ...

  10. FPGA---ucf文件语法

    1．约束文件的概念 FPGA设计中的约束文件有3类:用户设计文件(.UCF文件).网表约束文件(.NCF文件)以及物理约束文件(.PCF文件),可以完成时序约束.管脚约束以及区域约束.3类约束文件的关 ...