素数筛法—时间复杂度O(n)

请你想出一个算法求出n以内(含n)的所有素数，要求算法的时间复杂度越小越好。

这里介绍一种算法——快速线性素数筛法（欧拉筛法），时间复杂度O(n)。

诀窍在于：筛除合数时，保证每个合数只会被它的最小质因数筛去。因此每个数只会被标记一次，所以算法时间复杂度为O(n)。

具体请看下面的代码，主要函数是Prime(n)。

 #include <bits/stdc++.h>

 using namespace std;

 vector<int> Prime(int n) {  // 求解n以内(含n)的素数
     bool flag[n + ];   // 标记数组,flag[i]==0表示i为素数,flag[i]==1表示i为合数
     memset(flag, , sizeof(flag));
     vector<int> prime;
     int cnt = ;    // 素数个数
     for (int i = ; i <= n; ++i) {
         if (!flag[i]) {
             prime.push_back(i); // 将i加入素数表
             cnt++;
         }
         for (int j = ; j < cnt; ++j) { // 保证每个合数只会被它的最小质因数筛去
             if (i * prime[j] > n)  break;
             flag[i * prime[j]] = ;
             if (i % prime[j] == )  break;
         }
     }
     return prime;
 }
 int main(int argc, char const *argv[])
 {
     int n;
     while() {
         printf("请输入n,将输出n以内(含n)的素数:");
         scanf("%d", &n);
         if(n < ) break;
         vector<int> prime = Prime(n);
         int cnt = prime.size();
         printf("一共有%d个素数:\n", cnt);
         for(int i = ; i < cnt; i++) {
             printf("%3d ", prime[i]);
             if(i %  == ) puts("");
         }
         puts("\n");
     }
     return ;
 }

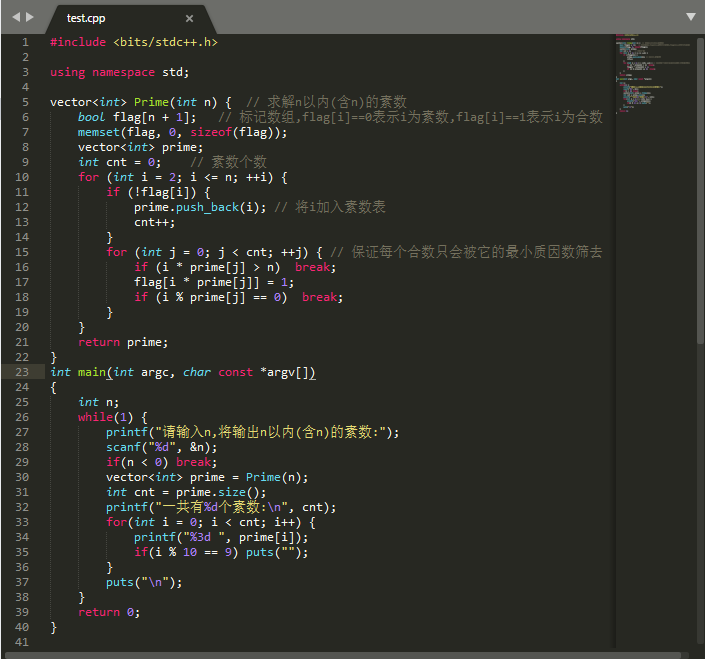
演示结果为：