车站分级 （2013noip普及组T4）（树形DP）

题目描述

一条单向的铁路线上，依次有编号为 1,2,…,n 的 n个火车站。每个火车站都有一个级别，最低为 1 级。现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站 x ，则始发站、终点站之间所有级别大于等于火车站 x 的都必须停靠。（注意：起始站和终点站自然也算作事先已知需要停靠的站点）

例如，下表是 5 趟车次的运行情况。其中，前 4 趟车次均满足要求，而第 5 趟车次由于停靠了 3 号火车站（ 2 级）却未停靠途经的 6 号火车站（亦为 2 级）而不满足要求。

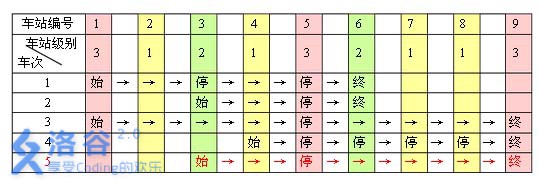
现有 m 趟车次的运行情况（全部满足要求），试推算这 n 个火车站至少分为几个不同的级别。

输入输出格式

输入格式：

第一行包含 2 个正整数 n,m，用一个空格隔开。

第 i+1 行 (1≤i≤m) 中，首先是一个正整数 si(2≤si≤n) ，表示第 i 趟车次有 si 个停靠站；接下来有 si 个正整数，表示所有停靠站的编号，从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。

输出格式：

一个正整数，即 n个火车站最少划分的级别数。

思路：

这么多巨佬在上，我这个蒟蒻也只能来一发树形DP了（其实好像是森林DP因为我懒得建超级根节点了）

很多大佬都用了拓扑排序，这是个好思想，但我太弱了不会用

我的这个树形DP的连边和很多大佬很像，每一条线路分别处理

如果某个点在起点到终点范围内，且没有停靠，由题意可知，这几站一定比停靠站的等级低，我就从停靠的站向不停靠的站连边，表示大小关系，当然，我不连重边

然后我开始遍历一遍所有的点，如果这个点没有入边，就说明它可能是最大的，我从这个点跑树形DP，每上升一层，大小+1，我们用动规找到最大层数，就是这个根点的答案

当然，我要求的是全图层数，当然要写一个max来比较了。

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#define rii register int i
#define rij register int j
using namespace std;
struct cz{
    int rd,cd,to[];
}x[];
int n,bj[],ans,tk[],bs,kkk,ltt,m,gh[][],as[],sf[];
void jb(int bh)
{
    x[bh].rd+=ltt;
    for(rii=;i<=ltt;i++)
    {
        if(gh[bh][tk[i]]==)
        {
            bs++;
            x[tk[i]].cd++;
            x[tk[i]].to[x[tk[i]].cd]=bh;
            gh[bh][tk[i]]=;
        }
    }
}
void dplast(int wz)
{
    for(rii=;i<=x[wz].cd;i++)
    {
        if(sf[x[wz].to[i]]==)
        {
            dplast(x[wz].to[i]);
            sf[x[wz].to[i]]=;
        }
        as[wz]=max(as[wz],as[x[wz].to[i]]+);
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(rii=;i<=m;i++)
    {
        int st,fi;
        memset(bj,,sizeof(bj));
        scanf("%d",&ltt);
        for(rij=;j<=ltt;j++)
        {
            scanf("%d",&kkk);
            tk[j]=kkk;
            bj[kkk]=;
            if(j==)
            {
                st=kkk;
            }
            if(j==ltt)
            {
                fi=kkk;
            }
        }
        for(rij=st+;j<fi;j++)//建边
        {
            if(bj[j]==)
            {
                jb(j);
            }
        }
    }
    for(rii=;i<=n;i++)
    {
        if(x[i].cd==)//初始化，如果是叶子节点，就不需要向下寻找，层数默认是1
        {
            as[i]=;
            sf[i]=;
        }
    }
    int maxn=;
    for(rii=;i<=n;i++)
    {
        if(x[i].rd==)
        {
            dplast(i);
        }
    }
    for(rii=;i<=n;i++)
    {
        maxn=max(maxn,as[i]);
    }
    cout<<maxn;
}