SVM主体思路和代码实现

　　之前学习的KNN算法属于直接将所有的训练图片数据化，根据图片的像素值进行判断，最简单的NN算法是用与待判断图片的差距最小（距离最近）的那张图片的类别当做此图片的类别，我们不难看到，1NN算法的正确性很差，相较于完全随机的10%的正确率，其正确率也不过只有20%左右，正确率低。我们用KNN算法则是用与其临近的K张图图片进行“投票”，得票最多的类别即为此图片的类别，可以看到，KNN算法有效的排除了某些噪声的干扰，但是主体的思路仍然是直接进行比较，此算法的缺点在于时间复杂度高，即每次判断一张新图片时，我们都需要遍历所有的训练数据，将训练数据的值与待判断题图片的像素值进行比较，而且十分不精确。

　　SVM算法的特点是需要模型需要经过长时间的训练（例如在本次实践中，训练模型就花了2.5分钟，这还仅仅是在数据规模不是很大的情况下），而之前的KNN不需要任何的训练和迭代过程，所谓的训练，仅仅是将所有的像素值都存在了一个矩阵中进行比较而已。但是SVM的判断过程极其迅速，只需要做一个矩阵乘法，然后找到其中分数最高的类就可以实现，不需要遍历整个训练集，能够更为方便的判断数据，这是SVM相较于KNN在时间性能上比较优秀的地方，此外，在算法的正确性方面，SVM跟KNN比较也有了长足的进步，以下将说明SVM的整个代码流程：

　　首先：与KNN一样，我们需要将输入的训练集（共有N个元素，M个类）抽象为矩阵存储，然后得到了训练矩阵（N*M），我们通过对训练矩阵进行某种操作，得到一个新的矩阵（W）。此矩阵就是我们计算机所产生的线性分类器模型，对于每一个输入的图片（一个行向量或者一个列向量），我们期望将输入的图片做一个变换（与线性分类器相乘），得到变换后的向量，此向量共有M个元素，每个元素体现了不同的类的得分情况。我们认为，图片在某一类分数越高，则属于这一类的可能性就越大。不妨看下面的图片

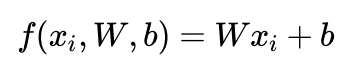
（摘自CS231N的课程笔记）

　　其中b为偏置向量，我们可以考虑为y=kx+b中的b，b不同，则与y轴的截距不同。这样起到的作用是能够让我们的分类器在划出决策边界时可以上下移动，增强其泛化能力。在这个算法中，我们显然期望原本的类别的得分应该尽可能高，事实上，我们后续在线性分类做决策时也是根据这个得分做决策的。但是显然，并不是所有的时候正确的类别的分数都是最高的，像这个例子，本来是猫，但是猫的得分反而是最低的。对于单一照片的分类我们可以认为是偶然的误差，可是我们希望在所训练出的模型尽可能多的满足此项规律，即正确项得分最高，换言之，我们不希望在训练模型的过程中丢失训练样本原本的信息，希望尽可能的保有原来的信息。那么如何衡量我们的训练过后的model是否丢失了一些信息呢？我们就引入一个概念叫做损失函数：损失函数顾名思义，是衡量我们预测值与初始值相差的函数，我们想要知道在训练中到底损失了多少信息，即可以用损失函数来衡量，损失函数有SVM和softmax两种，本篇仅仅讨论SVM损失函数：

　　　　

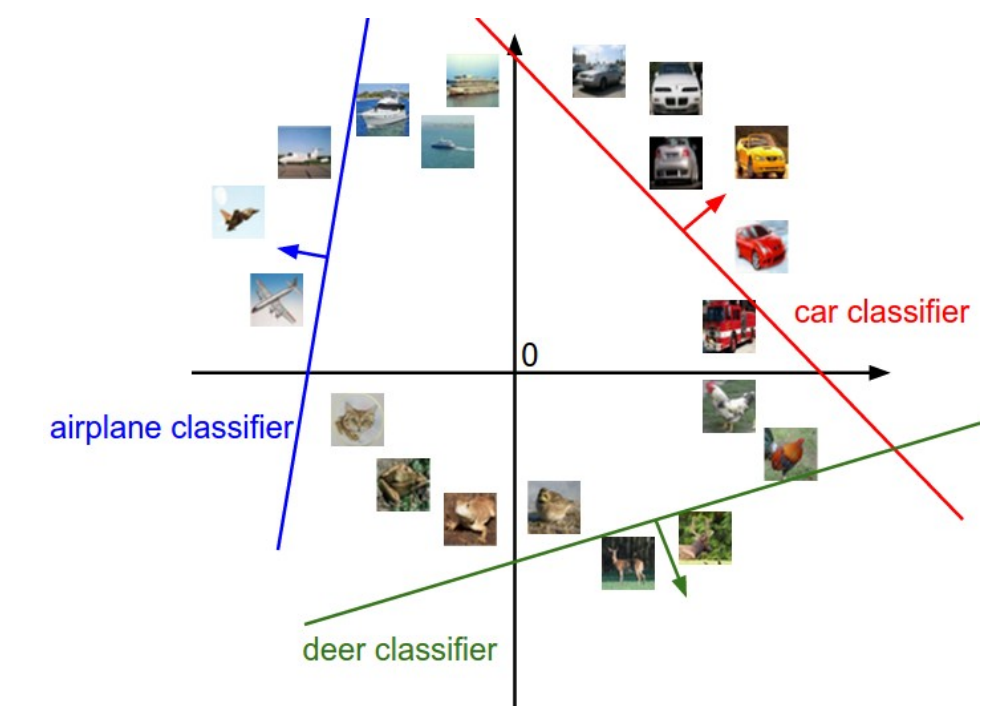
　　我们考虑，对于一个具体的图片，其所属类别一定是确定的，在坐标系中，即在决策边界的外侧，那么我们该如何衡量我们的损失呢？显然，如果我们在经过变换后得到不同类别的分数，此分数可以作为决策依据，那么我们很自然的考虑到如果正确类别的分数要高于其他类别，而且分数高出一个安全的边界，那么这种情况下，我们显然就十分满意，因为我们有充足的理由相信，这个图片我们判断的是对的，那么如果这张图片是我们的训练集中的元素，则可以认定为：我们训练出的model并没有磨灭掉其信息，其属性仍然存在，那么此时，我们就认为没有损失。由上面的文字叙述，我们可以得到以下的数学表达式：

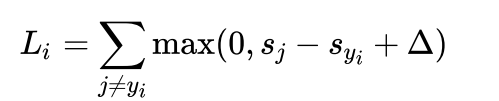
　　其中，Li即为对于第i个样例的损失函数，值得注意的是，我们规定了j≠yi是因为我们需要判断正确的类与错误类的得分差，正确类在这里起到的是比较作用，j＝yi的情况没有意义！

　　

　　我们希望尽可能多的数据，其错误类别都要尽可能的在绿色区域，而正确类别的分数都要尽可能在蓝色区域，那么此时正确和错误的差就有一个安全的delta，此时我们就不需要积累损失，显然，损失函数衡量了我们对于原本训练数据的正确性的满意程度，或者说损失了多少信息。显然，我们接下来要做的就是尽可能的减少损失函数，当然最优的可能性是损失函数恰好为0，即没有损失任何信息！但是显然我们遇到了一个问题，那就是可能不只有一个W符合我们的要求，如果有一个W能够完美符合我们所有的要求，即损失函数为0，那么对于W的任意倍数也都满足这个条件，显然是因为我们SVM损失函数所看中的，仅仅是数据之间的绝对差异。为了解决W不确定的问题，我们引入正则项的概念，正则项可以起到简化模型的作用。我们希望用一些偏好去唯一确定W，我们可以采取用正则惩罚项R（W）扩大损失值的方法：最常见的正则化惩罚是平方l2范数，它通过对所有元素二次惩罚来阻止大的权值：

　　于是我们的损失函数可以定义为一下的样子：

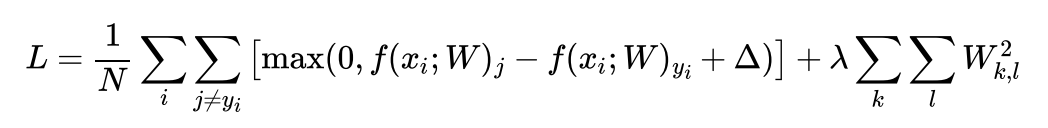
　　值得注意的是，前面的部分为所有损失函数的平均值，后面为正则项。我们期望上面的式子达到最小值，观察上式不难发现：有几个超参数，其中一个为W，还有一个安全边界delta（实际上delta=1即可，具体证明过程参见cs231n的课程介绍），另一个则是正则惩罚项的系数λ。我们可以采用K折交叉验证的方式去确定λ超参数。显然，不同的超参数的取值显著性的影响了我们分类器的性能，也即分类的准确性，那么接下来我们需要确定W到底该如何选取。

　　我们可以采用动态的方式去确定W，具体的实现思路如下：我们可以先随机一个W矩阵，里面的元素完全随机，然后计算出此时的损失函数值以及当前的梯度。我们考虑梯度下降法（SGD），假定我们在一个山谷中，我们想要往山下走，我们显然最容易想到的办法就是，找到当前位置最陡的地方，然后迈开步子往下走，每次走之前，都调整方向为最陡的地方，那么显然我们可以走到山底。此算法的思想也同样。我们计算出当前的梯度，然后每次往梯度的相反方向移动一定的步长，移动一定次数。每次移动完得到一个新的损失函数，与当前存储最优的损失值比较，如果当前的更优，则更新。