Coursera在线学习---第七节.支持向量机(SVM)

一、代价函数

 

　　对比逻辑回归与支持向量机代价函数。

　　cost1(z)=-log(1/(1+e^-z))　　　　　　cost0(z)=-log(1-1/(1+e^-z))

---

二、支持向量机中求解代价函数中的C值相当于1/λ。

　　如果C值过大，相当于λ过小，容易过拟合

　　如果C值过小，相当于λ过大，容易欠拟合。

三、大间隔分类(large margin classification)

　　两个向量的内积等于一个向量的长度乘以另一个向量在该向量的投影长度。

　　如下图：v*u=||u||*p。||u||为向量u的长度，p为向量v在u向量上的投影长度。

SVM代价函数求最优解，就是在约束条件下求极值的过程。如下图所示：

---

　　也就是在参数向量Θ与样本集X内积都≥1的情况下，使得Θ的长度最小。这种情况下只要离分类间隔面最近的样本点与Θ的内积为1就满足了约束条件，然后再求使得Θ的长度最小。

---

　　

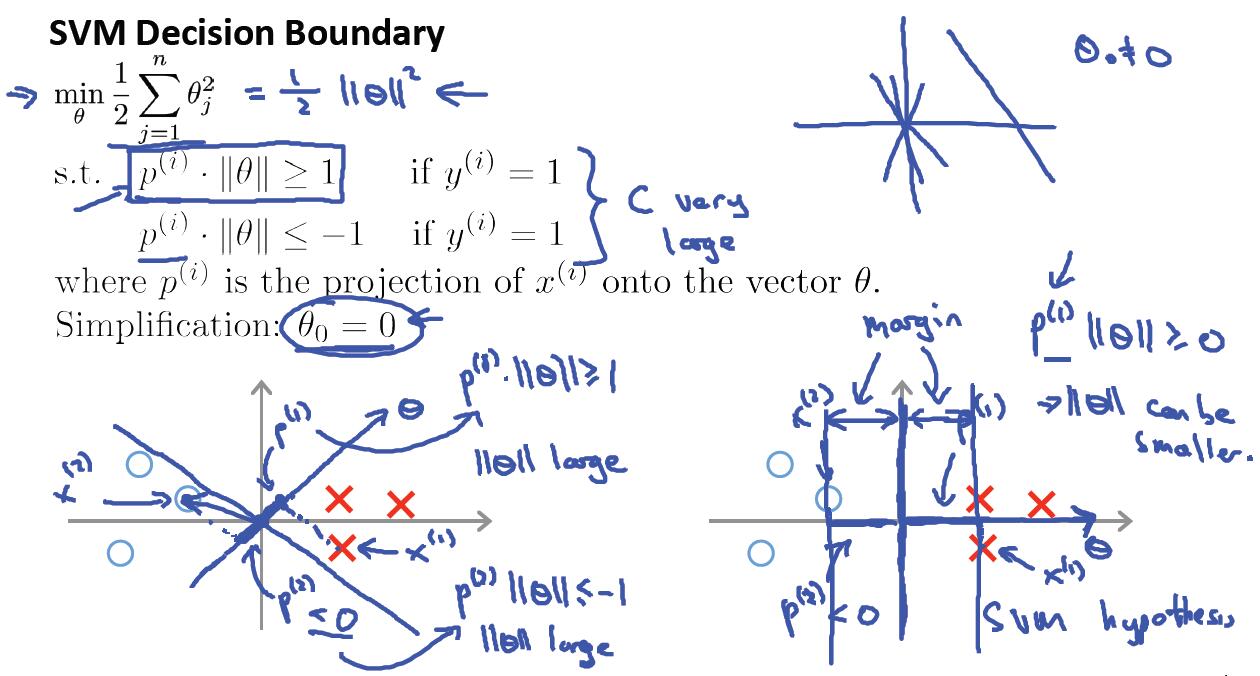
如上图所示，只有Θ的向量方向旋转到水平方向的时候，最近样本到Θ向量的投影长度才最长，这样才会使得Θ的值最小，因为二者的内积是固定为1的。而最大分类间隔面就是Θ的垂直平面，因为Θ与X组成的分类平面方程中，Θ与法向量方向是一样，法向量是垂直于平面的。

四、高斯核函数

五、高斯核函数中σ^2的选择

　　σ^2过大，f变化比较平滑，较慢，容易造成高偏差

　　σ^2过小，f变化比较大，斜率大，容易造成高方差

　　

六、如何使用SVM？

　　1）可以使用现有的软件包，比如：liblinear、libsvm.但是你需要做的是：

　　　　①.选择参数C

　　　　②.选择核函数Kernel

　　　　③.选择σ^2

　　2)线性核函数=没有核函数，直接使用Θ0+Θ1*X1+Θ2*X2...

　　　　注：如果特征维度n比较大，而训练样本集m又比较小的情况下，就没有必要使用核函数，选择线性核函数即可。因为，如果样本很少，使用核函数的话，容易过拟合！

七、利用高斯核函数之前一定要先进行归一化处理，以防止在计算距离公式中由某一维度数值较大的特征来决定。

　　

八、什么时候用Logistic Regression ，什么时候用SVM?

　　1)当特征维度n>=m时，例如文本分类，词的特征维度可能达到10000以上，而样本数量m可能只有几百、几千等。这个时候建议使用Logistic Regression 或者无核函数SVM。因为样本很少的情况下，这两个就足以工作的很好，况且也没有足够多的数据来拟合非常复杂的非线性函数。

　　2）如果特征维度n比较小（比如：n=1~1000,m=10~10000），m是中等大小的话，可以使用带高斯核函数的SVM分类算法。

　　3）如果n较小，而m非常非常大的情况下（比如n=500，m=50000），此时用高斯核函数会非常非常慢。这个时候我们选择增加更多的特征，使n增大，然后使用Logistic Regression 或者无核函数SVM。

　　注：尽管这些问题神经网络也能处理，但是相比svm而言，训练时间要长一些，svm则快的多。另外，svm的优化问题是一个凸优化问题，一个好的svm软件包总能找到全局最小值或接近它的值，而神经网络有时候会出现局部最优解的问题。

九、为什么SVM对缺失数据敏感？

这里说的缺失数据是指缺失某些特征数据，向量数据不完整。SVM没有处理缺失值的策略（决策树有）。而SVM希望样本在特征空间中线性可分，所以特征空间的好坏对SVM的性能很重要。缺失特征数据将影响训练结果的好坏。