单层感知机_线性神经网络_BP神经网络

单层感知机

单层感知机基础总结很详细的博客

关于单层感知机的视频

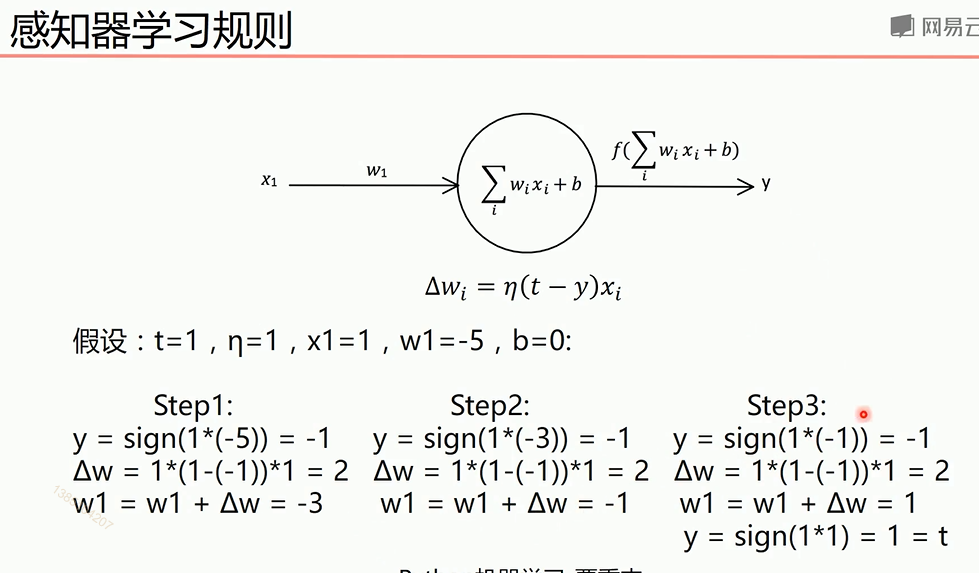
最终y=t,说明经过训练预测值和真实值一致。下面图是sign函数

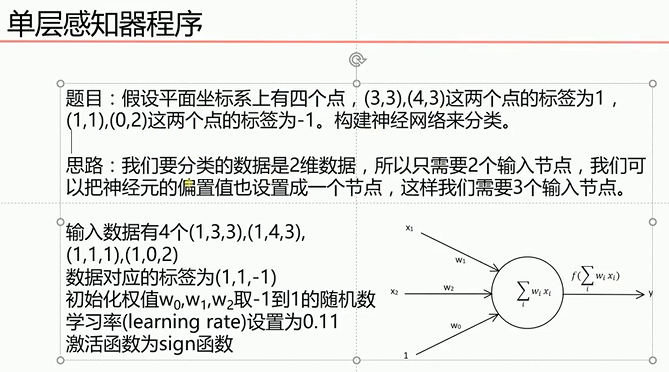
根据感知机规则实现的上述题目的代码

 import numpy as np
 import matplotlib.pyplot as plt
 #输入数据
 X = np.array([[,,],
               [,,],
               [,,],
               [,,]])
 #标签
 Y = np.array([[],
               [],
               [-],
               [-]])
 #权值初始化，3行1列，取值范围-1到1
 W = (np.random.random([,])-0.5)*
 print(W)
 #学习率设置
 lr = 0.11
 #神经网络输出
 O = 

 def update():
     global X,Y,W,lr
     O = np.sign(np.dot(X,W))
     W_C = lr*(X.T.dot(Y-O))/int(X.shape[])#除于样本个数目的是分子计算的误差是所有样本误差之和，所以要进行平均
     W = W + W_C
 for i in range():
     update()#更新权值
     print(W)
     print(i)
     O = np.sign(np.dot(X,W))
     if(O == Y).all():
         print('finished')
         print('epoch:',i)
         break
 #正样本
 x1 = [,]
 y1 = [,]
     #负样本
 x2 = [,]
 y2 = [,]

     #计算分界线的斜率以及截距
 k = -W[]/W[]
 d = -W[]/W[]
 print('k=',k)
 print('d=',d)

 xdata = (,)

 plt.figure()
 plt.plot(xdata,xdata*k+d,'r')
 plt.scatter(x1,y1,c='b')
 plt.scatter(x2,y2,c='y')
 plt.show()

单层感知机解决异或问题

 '''
 异或
 ^ =
 ^ =
 ^ =
 ^ =
 '''
 import numpy as np
 import matplotlib.pyplot as plt
 #输入数据
 X = np.array([[,,],
               [,,],
               [,,],
               [,,]])
 #标签
 Y = np.array([[-],
               [],
               [],
               [-]])

 #权值初始化，3行1列，取值范围-1到1
 W = (np.random.random([,])-0.5)*

 print(W)
 #学习率设置
 lr = 0.11
 #神经网络输出
 O = 

 def update():
     global X,Y,W,lr
     O = np.sign(np.dot(X,W)) # shape:(,)
     W_C = lr*(X.T.dot(Y-O))/int(X.shape[])
     W = W + W_C
 for i in range():
     update()#更新权值
     print(W)#打印当前权值
     print(i)#打印迭代次数
     O = np.sign(np.dot(X,W))#计算当前输出
     if(O == Y).all(): #如果实际输出等于期望输出，模型收敛，循环结束
         print('Finished')
         print('epoch:',i)
         break

 #正样本
 x1 = [,]
 y1 = [,]
 #负样本
 x2 = [,]
 y2 = [,]

 #计算分界线的斜率以及截距
 k = -W[]/W[]
 d = -W[]/W[]
 print('k=',k)
 print('d=',d)

 xdata = (-,)

 plt.figure()
 plt.plot(xdata,xdata*k+d,'r')
 plt.scatter(x1,y1,c='b')
 plt.scatter(x2,y2,c='y')
 plt.show()

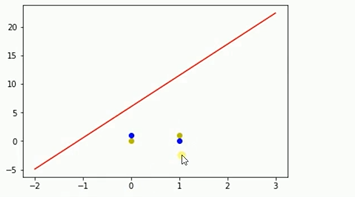
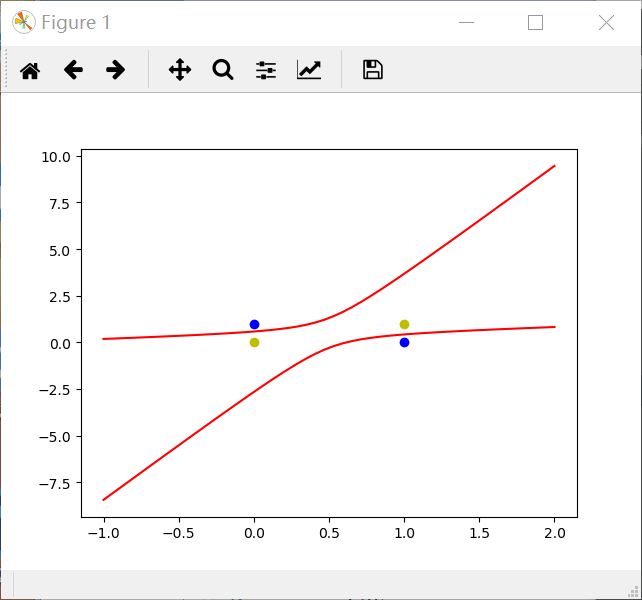
运行结果如上，可以知道单层感知机不适合解决如上类似的异或问题

线性神经网络

一篇优秀的线性神经网络博客总结链接

线性神经网络的学习视频

同时相比于感知机引入了Delta学习规则

解决感知机无法处理异或问题的方法

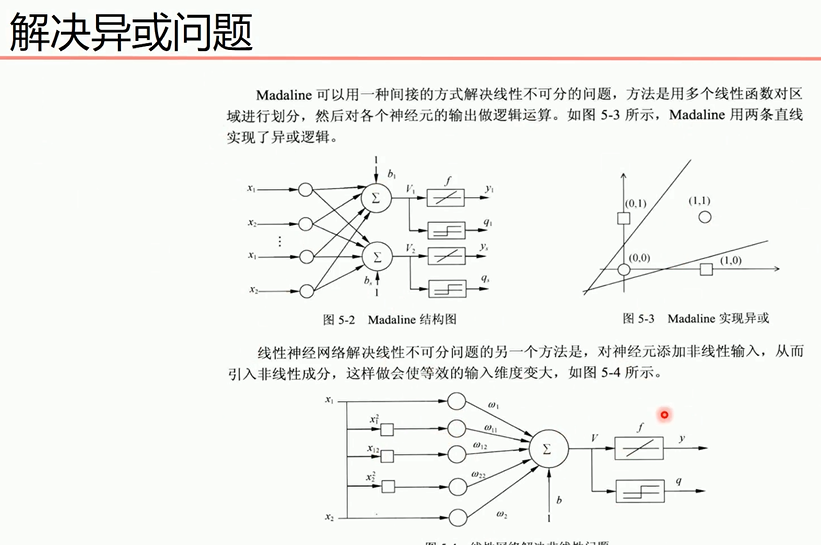
对于第二个方法

说明：X0是偏置值，值为1，X1，X2为线性输入，其它为添加的非线性输入，使用purelin激活函数（y=x）进行模型训练，再下面是y值的求法，用于图形绘制。

程序如下

 #题目：异或运算
 #^=
 #^=
 #^=
 #^=
 import numpy as np
 import matplotlib.pyplot as plt
 #输入数据--这里偏置定为1
 X = np.array([[,,,,,],
               [,,,,,],
               [,,,,,],
               [,,,,,]])
 #标签--期望输出
 Y = np.array([-,,,-])
 #权值初始化，1行6列，取-1到1的随机数
 W = (np.random.random()-0.5)*
 print(W)
 #学习率
 lr = 0.11
 #计算迭代次数
 n =
 #神经网络输出
 o = 

 def update():
     global X,Y,W,lr,n
     n+=
     o = np.dot(X,W.T)
     W_C = lr*((Y-o.T).dot(X))/(X.shape[])#权值改变数，这里除掉行数求平均值，因为行数多，权值改变就会很大。
     W = W + W_C
 for  i in range():
     update()#更新权值

 o = np.dot(X,W.T)
 print("执行一千次后的输出结果：",o)#看下执行一千次之后的输出

 #用图形表示出来
 #正样本
 x1 = [,]
 y1 = [,]
 #负样本
 x2 = [,]
 y2 = [,]

 def calculate(x,root):
     a = W[]
     b = W[]+x*W[]
     c = W[]+x*W[]+x*x*W[]
     if root == :#第一个根
         return (-b+np.sqrt(b*b-*a*c))/(*a)
     if root == :#第二个根
         return (-b-np.sqrt(b*b-*a*c))/(*a)

 xdata = np.linspace(-,)

 plt.figure()
 plt.plot(xdata,calculate(xdata,),'r')#用红色
 plt.plot(xdata,calculate(xdata,),'r')#用红色
 plt.plot(x1,y1,'bo')#用蓝色
 plt.plot(x2,y2,'yo')#用黄色
 plt.show()

 

利用神经网络解决上述感知机题目

 import numpy as np
 import matplotlib.pyplot as plt
 #输入数据
 X = np.array([[,,],
               [,,],
               [,,],
               [,,]])
 #标签
 Y = np.array([[],
               [],
               [-],
               [-]])

 #权值初始化，3行1列，取值范围-1到1
 W = (np.random.random([,])-0.5)*

 print(W)
 #学习率设置
 lr = 0.11
 #神经网络输出
 O = 

 def update():
     global X,Y,W,lr
     O = np.dot(X,W)
     W_C = lr*(X.T.dot(Y-O))/int(X.shape[])
     W = W + W_C
 for i in range():
     update()#更新权值

     #正样本
     x1 = [,]
     y1 = [,]
     #负样本
     x2 = [,]
     y2 = [,]

     #计算分界线的斜率以及截距
     k = -W[]/W[]
     d = -W[]/W[]
     print('k=',k)
     print('d=',d)

     xdata = (,)
     if i %  == :
         plt.figure()
         plt.plot(xdata,xdata*k+d,'r')
         plt.scatter(x1,y1,c='b')
         plt.scatter(x2,y2,c='y')
         plt.show()

BP神经网络

视频链接

反向传播（Back Propagation，简称BP）神经网络解决了多层神经网络的学习问题，广泛应用于分类识别、图像识别、压缩、逼近以及回归等领域，其结构如下所示。

另外介绍及格激活函数：sigmoid、tanh和softsign。神经网络中的激活函数，其作用就是引入非线性。
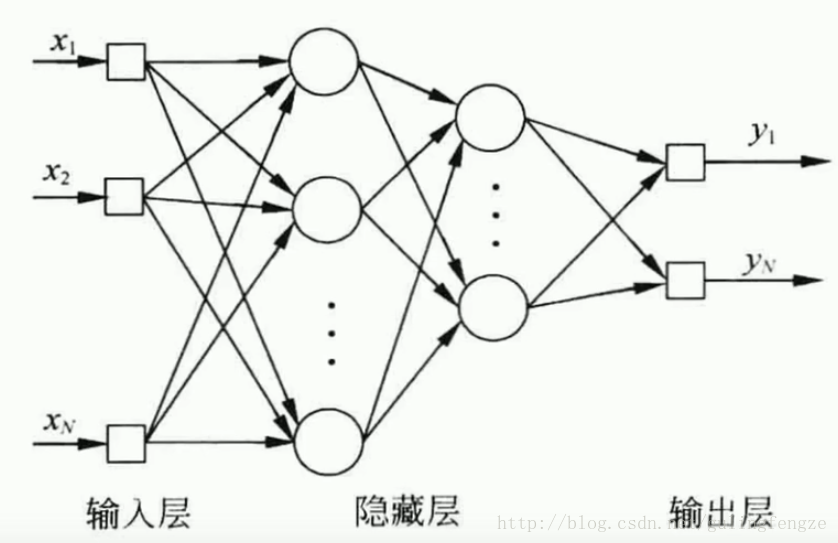
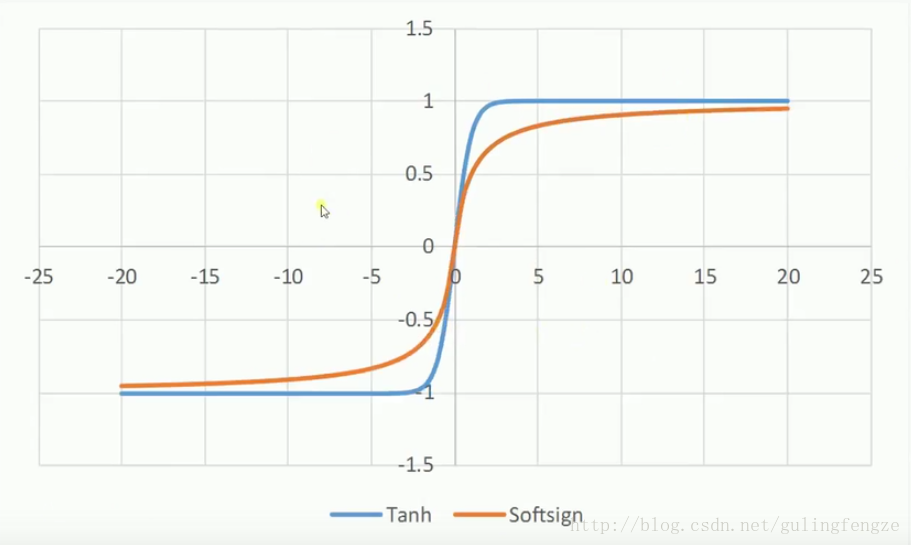
Sigmoid：sigmoid的优点是输出范围有限，数据在传递的过程中不容易发散，求导很容易（y=sigmoid(x), y’=y(1-y)）。缺点是饱和的时候梯度太小。其输出范围为(0, 1)，所以可以用作输出层，输出表示概率。
 
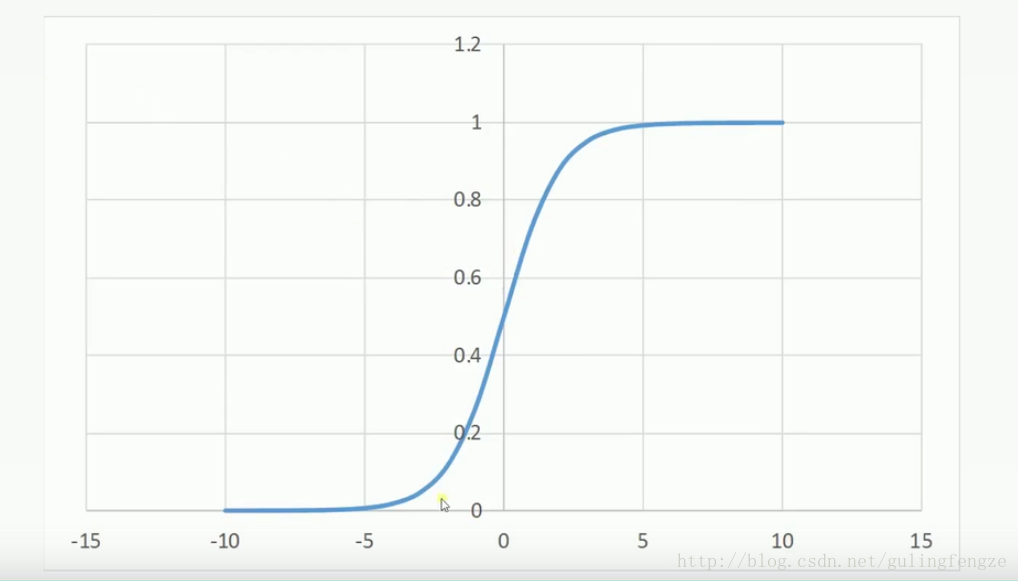
公式：

tanh和softsign：

要注意的是对多层神经元先对最后一层权重更新，其结果再更新前一层的权重

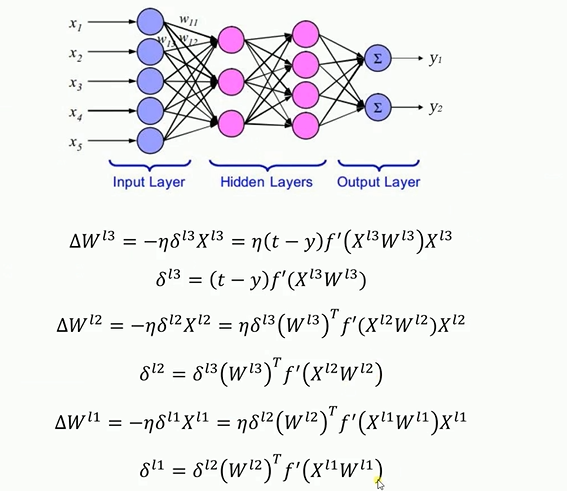
bp神经网络解决异或问题的程序如下

 import numpy as np

 # 输入数据
 X = np.array([[, , ],
               [, , ],
               [, , ],
               [, , ]])
 # 标签
 Y = np.array([[, , , ]])
 # 权值初始化，取值范围-1到1
 V = np.random.random((, )) *  -
 W = np.random.random((, )) *  -
 print(V)
 print(W)
 # 学习率设置
 lr = 0.11
 def sigmoid(x):
     return  / ( + np.exp(-x))
 def dsigmoid(x):
     return x * ( - x)#激活函数的导数
 def update():
     global X, Y, W, V, lr

     L1 = sigmoid(np.dot(X, V))  # 隐藏层输出(,)
     L2 = sigmoid(np.dot(L1, W))  # 输出层输出(,)

     L2_delta = (Y.T - L2) * dsigmoid(L2)
     L1_delta = L2_delta.dot(W.T) * dsigmoid(L1)

     W_C = lr * L1.T.dot(L2_delta)
     V_C = lr * X.T.dot(L1_delta)

     W = W + W_C
     V = V + V_C

 for i in range():
     update()  # 更新权值
     if i %  == :
         L1 = sigmoid(np.dot(X, V))  # 隐藏层输出(,)
         L2 = sigmoid(np.dot(L1, W))  # 输出层输出(,)
         print('Error:', np.mean(np.abs(Y.T - L2)))

 L1 = sigmoid(np.dot(X, V))  # 隐藏层输出(,)
 L2 = sigmoid(np.dot(L1, W))  # 输出层输出(,)
 print(L2)

 def judge(x):
     if x >= 0.5:
         return
     else:
         return 

 for i in map(judge, L2):
     print(i)