JavaScript图形实例：随机SierPinski三角形

在“JavaScript图形实例：SierPinski三角形”中，我们介绍了SierPinski三角形的基本绘制方法，在“JavaScript图形实例：迭代函数系统生成图形”一文中，介绍了采用IFS方法生成SierPinski三角形的方法。下面再介绍两种SierPinski三角形的构造方法，以扩展知识面。

1．随机点法

采用随机点的方法可以得到SierPinski三角形。具体过程为：

（1）任意取平面上三点A、B、C，组成一个三角形，并任意取三角形ABC内的一点P；

（2）求出P和A、B、C三个顶点中任意一个顶点的中点P1；

（3）描出该中点P1；

（4）将P1作为新的P点，转步骤（2），直到描出的点数达到规定要求（如10000个点）。

按上述思想，编写如下的HTML文件。在编程时，为简单计，不保证初始的P点一定在三角形ABC内（有可能在三角形外会描出几个散点，但不影响最后结果），也没有判断A、B、C三点可能共线的情况（此时无法构成三角形）。有兴趣的读者可以自行处理这两种情况，以完善代码。

<!DOCTYPE html>

<head>

<title>随机SierPinski三角形</title>

</head>

<body>

</canvas>

var canvas=document.getElementById('myCanvas');

var ctx=canvas.getContext('2d');

function draw()

{

ctx.fillStyle="#EEEEFF";

ctx.fillRect(0,0,300,300);

ctx.fillStyle="red";

ctx.font="32px";

var ax=Math.floor(Math.random()*200+50);

var ay=Math.floor(Math.random()*200+50);

var bx=Math.floor(Math.random()*200+50);

var by=Math.floor(Math.random()*200+50);

var cx=Math.floor(Math.random()*200+50);

var cy=Math.floor(Math.random()*200+50);

var px=Math.floor(Math.random()*200+50);

var py=Math.floor(Math.random()*200+50);

var dx=0;

var dy=0;

for (i=0; i<10000; i++)

{

index =Math.floor(Math.random()*3+1);

if (index==1)

{

dx = (ax + px)/2;

dy = (ay + py)/2;

}

else if (index == 2)

{

dx = (bx + px)/2;

dy = (by + py)/2;

}

else

{

dx = (cx + px)/2;

dy = (cy + py)/2;

}

ctx.fillText('.',dx,dy);

px = dx;

py = dy;

}

draw();

</script>

</body>

</html>

在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出一个SierPinski三角形，如图1所示。

图1 SierPinski三角形

将程序中的调用语句“draw()”改写为“window.setInterval('draw()', 1500);”，则在浏览器窗口中会每隔1.5秒绘制一个随机SierPinski三角形，如图2所示。

图2 每隔1.5秒绘制一个随机SierPinski三角形

由图2可以看出，有些三角形太小，设置有些成一条直线，因此，可以改写上面的程序，要求随机取点A、B、C时，保证三个边长均大于100，且三点不共线。改写的HTML文件内容如下。

<!DOCTYPE html>

<head>

<title>随机SierPinski三角形</title>

</head>

<body>

</canvas>

var canvas=document.getElementById('myCanvas');

var ctx=canvas.getContext('2d');

function draw()

{

ctx.fillStyle="#EEEEFF";

ctx.fillRect(0,0,300,300);

ctx.fillStyle="red";

ctx.font="32px";

while (1)

{

var ax=Math.floor(Math.random()*200+50);

var ay=Math.floor(Math.random()*200+50);

var bx=Math.floor(Math.random()*200+50);

var by=Math.floor(Math.random()*200+50);

var cx=Math.floor(Math.random()*200+50);

var cy=Math.floor(Math.random()*200+50);

ab=Math.sqrt((bx-ax)*(bx-ax)+(by-ay)*(by-ay));

ac=Math.sqrt((cx-ax)*(cx-ax)+(cy-ay)*(cy-ay));

bc=Math.sqrt((cx-bx)*(cx-bx)+(cy-by)*(cy-by));

if (ab<100 || ac<100 || bc<100) continue;

if (ab+bc==ac || ab+ac==bc || ac+bc==ab) continue;

var px=Math.floor(Math.random()*200+50);

var py=Math.floor(Math.random()*200+50);

break;

}

var dx=0;

var dy=0;

for (i=0; i<10000; i++)

{

index =Math.floor(Math.random()*3+1);

if (index==1)

{

dx = (ax + px)/2;

dy = (ay + py)/2;

}

else if (index == 2)

{

dx = (bx + px)/2;

dy = (by + py)/2;

}

else

{

dx = (cx + px)/2;

dy = (cy + py)/2;

}

ctx.fillText('.',dx,dy);

px = dx;

py = dy;

}

window.setInterval('draw()', 1500);

</script>

</body>

</html>

在浏览器中打开包含这段改写后的HTML代码的html文件，在浏览器窗口中也会每隔1.5秒绘制一个随机SierPinski三角形，如图3所示，此时每个随机SierPinski三角形的最小边长均会超过100，三角形不会显得较小。

图3 每隔1.5秒绘制一个较大的随机SierPinski三角形

上面程序中随机点法构造SierPinski三角形是描点10000个得到的。为展示描点过程，编写如下的HTML文件。

<!DOCTYPE html>

<head>

<title>随机SierPinski三角形</title>

</head>

<body>

</canvas>

var canvas=document.getElementById('myCanvas');

var ctx=canvas.getContext('2d');

ctx.fillStyle="#EEEEFF";

ctx.fillRect(0,0,400,400);

ctx.fillStyle="red";

ctx.font="32px";

while (1)

{

var ax=Math.floor(Math.random()*400);

var ay=Math.floor(Math.random()*400);

var bx=Math.floor(Math.random()*400);

var by=Math.floor(Math.random()*400);

var cx=Math.floor(Math.random()*400);

var cy=Math.floor(Math.random()*400);

ab=Math.sqrt((bx-ax)*(bx-ax)+(by-ay)*(by-ay));

ac=Math.sqrt((cx-ax)*(cx-ax)+(cy-ay)*(cy-ay));

bc=Math.sqrt((cx-bx)*(cx-bx)+(cy-by)*(cy-by));

if (ab<200 || ac<200 || bc<200) continue;

if (ab+bc==ac || ab+ac==bc || ac+bc==ab) continue;

var px=Math.floor(Math.random()*400);

var py=Math.floor(Math.random()*400);

break;

}

var i=0;

function draw()

{

index =Math.floor(Math.random()*3+1);

if (index==1)

{

dx = (ax + px)/2;

dy = (ay + py)/2;

}

else if (index == 2)

{

dx = (bx + px)/2;

dy = (by + py)/2;

}

else

{

dx = (cx + px)/2;

dy = (cy + py)/2;

}

ctx.fillText('.',dx,dy);

px = dx;

py = dy;

i++;

if (i>=10000)

{

ctx.fillStyle="#EEEEFF";

ctx.fillRect(0,0,400,400);

ctx.fillStyle="red";

i=0;

}

window.setInterval('draw()',1);

</script>

</body>

</html>

在浏览器中打开包含这段HTML代码的html文件，在浏览器窗口中呈现出一个随机SierPinski三角形的喷出过程，如图4所示。

图4 随机SierPinski三角形的喷出过程

2．按组合数的奇偶性直接描点构造SierPinski三角形

设有如下的杨辉三角形，若将杨辉三角形的奇数处画圆点，偶数处留空，则会得到SierPinski三角形。

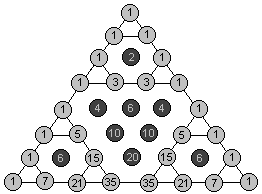
由于杨辉三角中第i行第j列的数字正是组合数C（i,j）的结果。因此，对杨辉三角形中各行各列数字的讨论转化为对组合数C(n,m)的讨论。

组合数的奇偶性判定方法为:

对于C(n,m)，若n&m == m 则C(n,m)为奇数，否则为偶数。

根据这个结论，直接编写如下的HTML文件。

<!DOCTYPE html>

<head>

<title>按组合数奇偶性构造SierPinski三角形</title>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var ctx=canvas.getContext('2d');

ctx.fillStyle="#EEEEFF";

ctx.fillRect(0,0,300,300);

ctx.fillStyle="red";

for (i=0;i<256;i++)

{

for (j=0;j<=i;j++)

if ((i&j)==j)

ctx.fillText('.',j+30,i+30);

}

</script>

</head>

</canvas>

</body>

</html>

在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出如图5所示的SierPinski三角形。

图5 SierPinski三角形