算法笔记_224:夺冠概率模拟(Java)

目录

1 问题描述

2 解决方案

 

---

1 问题描述

足球比赛具有一定程度的偶然性，弱队也有战胜强队的可能。

假设有甲、乙、丙、丁四个球队。根据他们过去比赛的成绩，得出每个队与另一个队对阵时取胜的概率表:

甲 乙 丙 丁
甲 - 0.1 0.3 0.5
乙 0.9 - 0.7 0.4
丙 0.7 0.3 - 0.2
丁 0.5 0.6 0.8 -

数据含义：甲对乙的取胜概率为0.1，丙对乙的胜率为0.3，...

现在要举行一次锦标赛。双方抽签，分两个组比，获胜的两个队再争夺冠军。（参见【1.jpg】）

请你进行10万次模拟，计算出甲队夺冠的概率。

注意：

请仔细调试！您的程序只有能运行出正确结果的时候才有机会得分！

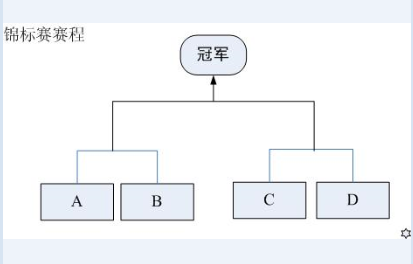
图1

---

2 解决方案

 public class Main {
 
     public static void main(String[] args) {
         double[][] value = {{0, 0.1, 0.3, 0.5},
                 {0.9, 0, 0.7, 0.4},
                 {0.7, 0.3, 0, 0.2},
                 {0.5, 0.6, 0.8, 0}};
         double[] result = new double[100000];
         double sum = 0;
         for(int i = 0;i < 100000;i++) {
             int a = (int) (Math.random() * 3) + 1; //甲的对手
             if(a == 1)
                 result[i] = value[0][1] * value[2][3] * value[0][2] +
                     value[0][1] * value[3][2] * value[0][3];
             else if(a == 2)
                 result[i] = value[0][2] * value[1][3] * value[0][1] +
                     value[0][2] * value[3][1] * value[0][3];
             else
                 result[i] = value[0][3] * value[1][2] * value[0][1] +
                     value[0][3] * value[2][1] * value[0][2];
             sum = sum + result[i];
         }
         sum = sum / 100000;
         System.out.printf("%.3f", sum);
     }
 }

运行结果：

0.076