1066. Root of AVL Tree (25)

An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.

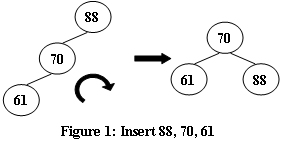
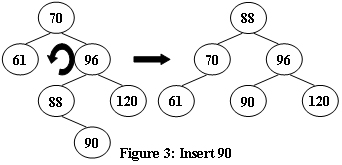
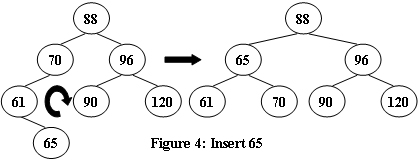
Now given a sequence of insertions, you are supposed to tell the root of the resulting AVL tree.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (<=20) which is the total number of keys to be inserted. Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print ythe root of the resulting AVL tree in one line.

Sample Input 1:

5
88 70 61 96 120

Sample Output 1:

70

Sample Input 2:

7
88 70 61 96 120 90 65

Sample Output 2:

88

 #include<stdio.h>
 #include<vector>
 #include<algorithm>
 using namespace std;

 struct node
 {
     node(int v):left(NULL),right(NULL),high(),val(v){}
     node* left,* right;
     int val,high;
 };

 int gethigh(node* root)
 {
     int a = , b = ;
     if(root->left!= NULL)
         a = root->left->high;
     if(root->right!= NULL)
         b = root->right->high;
     return a > b ? a+:b+;
 }

 void R(node* & root)
 {
     node* tem = root->left;
     root->left = tem->right;
     tem->right = root;
     root->high = gethigh(root);
     tem->high = gethigh(tem);
     root = tem;
 }

 void L(node* & root)
 {
     node* tem = root->right;
     root->right = tem->left;
     tem->left = root;
     root->high = gethigh(root);
     tem->high = gethigh(tem);
     root = tem;
 }

 void insert(node*& root,int val)
 {
     if(root == NULL)
     {
         root = new node(val);
         return;
     }

     if(val < root->val)
     {
         insert(root->left,val);
         root->high = gethigh(root);
         int a = root->left == NULL ?  : root->left->high;
         int b = root->right == NULL ?  : root->right->high;
         if(a - b == )
         {
             int c = root->left->left == NULL ? :root->left->left->high;
             int d = root->left->right == NULL ? :root->left->right->high;
             if(c - d  ==  )
             {
                 R(root);
             }
             else if(c - d  == -)
             {
                 L(root->left);
                 R(root);
             }
         }
     }
     else
     {
         insert(root->right,val);
         root->high = gethigh(root);
         int a = root->left == NULL ?  : root->left->high;
         int b = root->right == NULL ?  : root->right->high;
         if(a - b == -)
         {
             int c = root->right->right == NULL ? :root->right->right->high;
             int d = root->right->left == NULL ? :root->right->left->high;
             if(c - d == )
             {
                 L(root);
             }
             else if(c - d == -)
             {
                 R(root->right);
                 L(root);
             }
         }
     }
 }

 int main()
 {
     int n,tem;
     scanf("%d",&n);
     node* Tree = NULL;
     for(int i = ;i < n;++i)
     {
         scanf("%d",&tem);
         insert(Tree,tem);
     }
     printf("%d\n",Tree->val);
     return ;
 }