【转】Bresenham快速画直线算法

一、             算法原理简介：

算法原理的详细描述及部分实现可参考：

http://www.cs.helsinki.fi/group/goa/mallinnus/lines/bresenh.html

Fig.1

假设以(x, y)为绘制起点，一般情况下的直观想法是先求m = dy /dx（即x每增加1， y的增量），然后逐步递增x, 设新的点为x1 = x + j, 则y1 = round(y + j * m)。可以看到，这个过程涉及大量的浮点运算，效率上是比较低的（特别是在嵌入式应用中，DSP可以一周期内完成2次乘法，一次浮点却要上百个周期）。

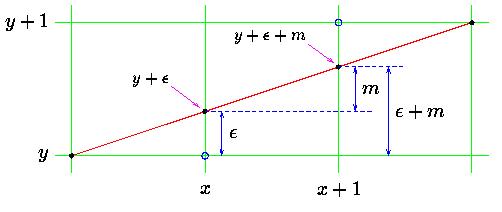
下面，我们来看一下Bresenham算法，如Fig. 1,(x, y +ε)的下一个点为(x, y + ε + m)，这里ε为累加误差。可以看出，当ε+m < 0.5时，绘制(x + 1, y)点，否则绘制(x + 1, y + 1)点。每次绘制后，ε将更新为新值：

ε = ε + m ,如果(ε + m) <０.５ (或表示为2*(ε + m) < 1)

ε = ε + m – 1, 其他情况

将上述公式都乘以dx, 并将ε*dx用新符号ξ表示，可得

ξ = ξ + dy, 如果2*(ξ + dy) < dx

ξ = ξ + dy – dx, 其他情况

可以看到，此时运算已经全变为整数了。以下为算法的伪代码：

ξ ← 0, y ← y1

For x ← x1 to x2 do

Plot Point at (x, y)

If (2(ξ + dy) < dx)

ξ ←ξ + dy

Else

y ← y + 1,ξ ←ξ + dy – dx

End If

End For

二、             算法的注意点：

Fig. 2

在实际应用中，我们会发现，当dy > dx或出现Fig.2 右图情况时时，便得不到想要的结果，这是由于我们只考虑dx > dy， 且x, y的增量均为正的情况所致。经过分析，需要考虑8种不同的情况，如Fig. 3所示：

当然，如果直接在算法中对8种情况分别枚举， 那重复代码便会显得十分臃肿，因此在设计算法时必须充分考虑上述各种情况的共性，后面将给出考虑了所有情况的实现代码。

三、             算法的实现

以下代码的测试是利用Opencv 2.0进行的,根据需要，只要稍微修改代码便能适应不同环境

//Code highlighting produced by Actipro CodeHighlighter (freeware)http://www.CodeHighlighter.com/
void DrawLine(IplImage *img, int x1, int y1, int x2, int y2)
{
     int dx = x2 - x1;
     int dy = y2 - y1;
     int ux = ((dx > ) << ) - ;//x的增量方向，取或-1
     int uy = ((dy > ) << ) - ;//y的增量方向，取或-1
     int x = x1, y = y1, eps;//eps为累加误差

     eps = ;dx = abs(dx); dy = abs(dy);
     if (dx > dy)
     {
         for (x = x1; x != x2; x += ux)
         {
              SetPixel(img, x, y);
              eps += dy;
              if ((eps << ) >= dx)
              {
                   y += uy; eps -= dx;
              }
         }
     }
     else
     {
         for (y = y1; y != y2; y += uy)
         {
              SetPixel(img, x, y);
              eps += dx;
              if ((eps << ) >= dy)
              {
                   x += ux; eps -= dy;
              }
         }
     }
}

四、             测试结果

五、             进一步可能的改进

设(x1, y1)为起点,(x2, y2)为终点，取中点(x1 + x2)/2, (y1 +y2)/2，然后从两个端点同时向中点生长，这种并行运算可以提高一定的效率。

原文地址：http://www.cnblogs.com/pheye/archive/2010/08/14/1799803.html