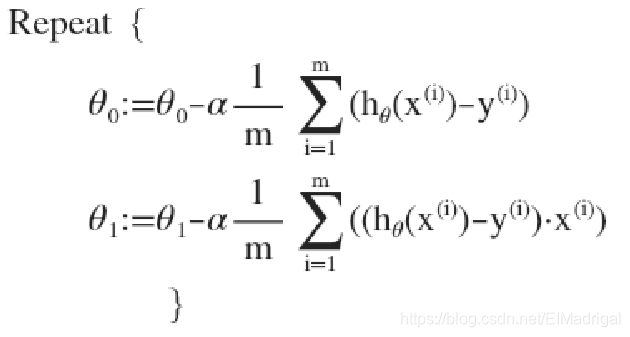#Week2 Linear Regression with One Variable
一、Model Representation
还是以房价预测为例,一图胜千言:
h表示一个从x到y的函数映射。
二、Cost Function
因为是单变量线性回归,所以假设函数是:
\]
所以接下来的问题是怎样确定参数\(\theta_0\)和\(\theta_1\)?
这两个参数会决定我们的模型预测值与训练集的实际数据的差距,这就是建模误差。
那么在回归问题中,代价函数选择如下的平方误差函数比较合理:
\]
m是训练集的样本数目,\(x^{(i)}\)是每个房子的尺寸,\(y^{(i)}\)是实际价格。
只要寻找使得\(J(\theta_0,\theta_1)\)最小的参数即可。
之所以要除以2,主要是为了后续的梯度下降法求导时抵消平方的那个2。
三、Gradient Descent
为了求得代价函数的最小值,采用梯度下降法。
- 用一个随机的参数组合计算\(J\)
- 找到一个使得\(J\)下降最多的参数组合,更新参数,直到找到一个局部最优解
就像下山一样,每次都走一步,每次选择下降最快的方向直到局部最低。
在批量梯度下降算法(所有的训练样本都要用到)中,同步更新所有参数:
\(\alpha\)是学习率,表示每一步走多长。
如果\(\alpha\)太小,那么更新的过程就会很缓慢;如果\(\alpha\)太大,可能跳过最低点,导致发散。
当接近局部最优时,由于斜率会越来越小,所以每一步会自动走得很小,不需要减小学习率\(\alpha\)。
四、Gradient Descent For Linear Regression
对之前得回归模型应用梯度下降算法:
对\(J(\theta_0,\theta_1)\)求关于\(\theta_0\)、\(\theta_1\)的偏导数,带入参数更新公式,有:
#Week2 Linear Regression with One Variable的更多相关文章
- Stanford机器学习---第二讲. 多变量线性回归 Linear Regression with multiple variable
原文:http://blog.csdn.net/abcjennifer/article/details/7700772 本栏目(Machine learning)包括单参数的线性回归.多参数的线性回归 ...
- Stanford机器学习---第一讲. Linear Regression with one variable
原文:http://blog.csdn.net/abcjennifer/article/details/7691571 本栏目(Machine learning)包括单参数的线性回归.多参数的线性回归 ...
- 机器学习笔记1——Linear Regression with One Variable
Linear Regression with One Variable Model Representation Recall that in *regression problems*, we ar ...
- Machine Learning 学习笔记2 - linear regression with one variable(单变量线性回归)
一.Model representation(模型表示) 1.1 训练集 由训练样例(training example)组成的集合就是训练集(training set), 如下图所示, 其中(x,y) ...
- Ng第二课:单变量线性回归(Linear Regression with One Variable)
二.单变量线性回归(Linear Regression with One Variable) 2.1 模型表示 2.2 代价函数 2.3 代价函数的直观理解 2.4 梯度下降 2.5 梯度下 ...
- 【cs229-Lecture2】Linear Regression with One Variable (Week 1)(含测试数据和源码)
从Ⅱ到Ⅳ都在讲的是线性回归,其中第Ⅱ章讲得是简单线性回归(simple linear regression, SLR)(单变量),第Ⅲ章讲的是线代基础,第Ⅳ章讲的是多元回归(大于一个自变量). 本文的 ...
- MachineLearning ---- lesson 2 Linear Regression with One Variable
Linear Regression with One Variable model Representation 以上篇博文中的房价预测为例,从图中依次来看,m表示训练集的大小,此处即房价样本数量:x ...
- 斯坦福第二课:单变量线性回归(Linear Regression with One Variable)
二.单变量线性回归(Linear Regression with One Variable) 2.1 模型表示 2.2 代价函数 2.3 代价函数的直观理解 I 2.4 代价函数的直观理解 I ...
- 机器学习 (一) 单变量线性回归 Linear Regression with One Variable
文章内容均来自斯坦福大学的Andrew Ng教授讲解的Machine Learning课程,本文是针对该课程的个人学习笔记,如有疏漏,请以原课程所讲述内容为准.感谢博主Rachel Zhang的个人笔 ...
随机推荐
- WTM asp.net core应用程序在Ubuntu上和CentOS上部署
wtm在Ubuntu上和CentOS上部署 项目发布 在Visual Studio中右击Web项目,选择发布,如下图: Ubuntu安装.net core运行时 Ubuntu我是用的Vmware虚拟机 ...
- MTK Android 权限大全
Android权限大全 1.android.permission.WRITE_USER_DICTIONARY允许应用程序向用户词典中写入新词 2.android.permission.WRITE_SY ...
- 2017蓝桥杯兴趣小组(C++C组)
原题:兴趣小组 为丰富同学们的业余文化生活,某高校学生会创办了3个兴趣小组(以下称A组,B组,C组).每个小组的学生名单分别在[A.txt],[B.txt]和[C.txt]中.每个文件中存储的是学生的 ...
- C语言中 sinx cosx 的用法
#include<stdio.h> #include<math.h> int main() { double pi=acos(-1.0); double ang ...
- 30.2 案例:ArrayList本身数据可以重复,写出去重的方法
package day30_HashSet; /* * ArrayList特点(实现List接口) 有序.可以重复.可以使用索引 *使用ArrayList实现数据去重 * */ import java ...
- centos7安装MariaDB以及Failed to start mariadb.service: Unit not found的错误解决
centos7下yum安装MariaDB CentOS 7下mysql下替换成MariaDB了.MariaDB数据库管理系统是MySQL的一个分支,主要由开源社区在维护,采用GPL授权 许可 Mari ...
- [原创] 在C++中实现打字机效果
如题. void pout(string str,int t)//随便取的,不要介意,str是待输出字符串,t是每两个字的间隔时间. { ;i<str.length();i++) { cout& ...
- 006-循环结构(下)-C语言笔记
006-循环结构(下)-C语言笔记 学习目标 1.[掌握]do-while循环结构 2.[掌握]for循环结构 3.[掌握]嵌套循环 一.do-while循环结构 do-while语法: 1 2 ...
- stand up meeting 12/4/2015 -12/6/2015
part 组员 今日工作 工作耗时/h 明日计划 工作耗时/h UI 冯晓云 ------ --- 数据库 朱玉影 等待张葳出关 0 foxit reader 6 ...
- jdbctemplate打印sql
在logback.xml里加入如下配置即可: <include resource="org/springframework/boot/logging/logback/base.xml& ...