LeetCode952三部曲之三：再次优化(122ms -＞ 96ms，超51% -＞ 超91%)

欢迎访问我的GitHub

这里分类和汇总了欣宸的全部原创(含配套源码)：https://github.com/zq2599/blog_demos

本篇概览

• 本文是《LeetCode952三部曲之三》的终篇，先回顾一下前文的成果，看看我们之前已经优化到什么程度：
  
  
• 前文的优化思路是减小并查集数组的规模，带来的结果是节省内存、减少数组相关的执行次数，但从代码上分析，并查集数组处理所占比重并不多，所以造成此处整体优化效果一般
• 所以，除了并查集，还要去寻找其他优化点，这就是本篇的主要内容

优化思路

• 寻找优化点的方向很明确：重点关注时间复杂度高的代码块
• 按照上述思路，很容易就找到了下图中的代码段，位于程序入口位置，计算每个数字的质因数，因为涉及到素数，所以时间复杂度较高，三个耗时操作是嵌套关系
  
  
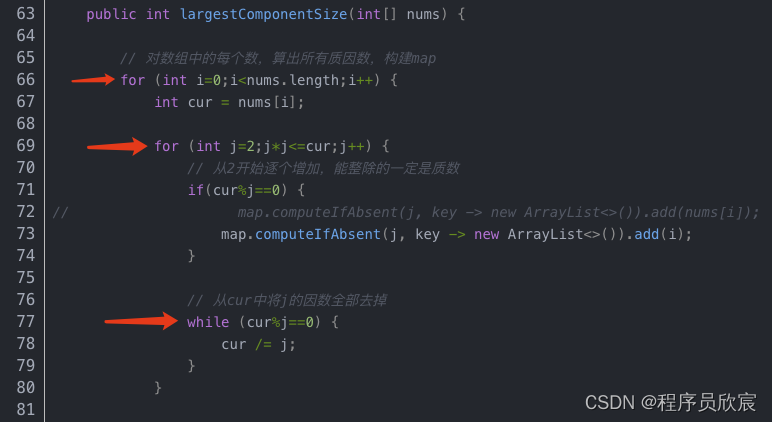
• 上述方法的思路对每个数字做计算，找出质因数，例如找出99的质因数，需要从2开始一次次计算得出
• 但实际上还有一个更简单的思路：99以内的质数是固定的25个，这25个中，其平方小于99的只有四个，既：2，3，5，7，所以寻找99的质即因数，就在这四个中找即可（漏掉的11，在后面的代码中会特别处理找回来）
• 基于以上思路，计算质因数的代码就很简单了：

1. 提前把100000以内的所有素数都找出来，放在名为primes的数组中
2. 对于任意一个数字N，都用primes中的数字去做除法，能整除的就是N的质因数
3. 记得像前面的99漏掉了11那样，把11找回来

编码

• 接下来的代码，在前文的基础上修改
• 首先增加三个静态变量，注释已详细说明其作用：

    // isPrime[3]=0，表示数字3是素数，isPrime[4]=1，表示数字4不是素数
    private static int[] isPrime = new int[100001];

    // 0-100001之间所有的素数都放入这里
    private static int[] primes = new int[100001];

    // 素数的数量，也就是primes中有效数据的长度
    private static int primeNum = 0;

• 然后是一个静态代码块，一次性算处100000范围内所有素数，埃式或者欧拉式都可以，这里用了欧拉式

static {

        // 欧拉筛
        for(int i=2;i<=100000;i++) {
            if(isPrime[i]==0) {
                // i是素数，就放入primes数组中
                // 更新primes中素数的数量
                primes[primeNum++] = i;
            }

            for(int j=0;i*primes[j]<=100000;j++) {
                // primes[j]*i的结果是个乘积，这样的数字显然不是素数，所以在isPrimes数组中标注为1
                isPrime[primes[j]*i] = 1;

                // 如果i是primes中某个素数的倍数，就没有必要再计算了，退出算下一个，
                // 例如i=8的时候，其实在之前i=4时就已经计算出8不是素数了
                if(i%primes[j]==0) {
                    break;
                }
            }
        }

        // 经过以上代码，0-100001之间所有素数都放入了primes中
    }

• 上述代码只会在类加载后执行一次，执行完毕后，1到100000之间的所有素数都计算出来并放入primes中，数量是primeNum，在后面的计算中直接拿来用即可
• 接下来是最关键的地方了，前面截图中对每个数字计算质因数的代码，可以替换掉了，新的代码如下，可见逻辑已经简化了，从数组primes中取出来做除法即可：

        // 对数组中的每个数，算出所有质因数，构建map
        for (int i=0;i<nums.length;i++) {
            int cur = nums[i];

            // cur的质因数一定是primes中的一个
            for (int j=0;j<primeNum && primes[j]*primes[j]<=cur;j++) {
                if (cur%primes[j]==0) {
                    map.computeIfAbsent(primes[j], key -> new ArrayList<>()).add(i);

                    // 要从cur中将primes[j]有关的倍数全部剔除，才能检查下一个素数
                    while (cur%primes[j]==0) {
                        cur /= primes[j];
                    }
                }
            }

            // 能走到这里依然不等于1，是因为for循环中的primes[j]*primes[j]<<=cur导致了部分素数没有检查到，
            // 例如6，执行了for循环第一轮后，被2除过，cur等于3，此时j=1,那么primes[j]=3，因此 3*3无法小于cur的3，于是退出for循环，
            // 此时cur等于3，应该是个素数，所以nums[i]就能被此时的cur整除，那么此时的cur就是nums[i]的质因数，也应该放入map
            if (cur>1) {
                map.computeIfAbsent(cur, key -> new ArrayList<>()).add(i);
            }
        }

• 另外，对于之前99取质因数漏掉了11的问题，上述代码也有详细说明：检查整除结果，大于1的就是漏掉的
• 完整的提交代码如下

package practice;

import java.util.*;

/**
 * @program: leetcode
 * @description:
 * @author: za2599@gmail.com
 * @create: 2022-06-30 22:33
 **/
public class Solution {

    // 并查集的数组， fathers[3]=1的意思是：数字3的父节点是1
//    int[] fathers = new int[100001];
    int[] fathers;

    // 并查集中，每个数字与其子节点的元素数量总和，rootSetSize[5]=10的意思是：数字5与其所有子节点加在一起，一共有10个元素
//    int[] rootSetSize = new int[100001];
    int[] rootSetSize;

    // map的key是质因数，value是以此key作为质因数的数字
    // 例如题目的数组是[4,6,15,35]，对应的map就有四个key：2,3,5,7
    // key等于2时，value是[4,6]，因为4和6的质因数都有2
    // key等于3时，value是[6,15]，因为6和16的质因数都有3
    // key等于5时，value是[15,35]，因为15和35的质因数都有5
    // key等于7时，value是[35]，因为35的质因数有7
    Map<Integer, List<Integer>> map = new HashMap<>();

    // 用来保存并查集中，最大树的元素数量
    int maxRootSetSize = 1;

    // isPrime[3]=0，表示数字3是素数，isPrime[4]=1，表示数字4不是素数
    private static int[] isPrime = new int[100001];

    // 0-100001之间所有的素数都放入这里
    private static int[] primes = new int[100001];

    // 素数的数量，也就是primes中有效数据的长度
    private static int primeNum = 0;

    static {

        // 欧拉筛
        for(int i=2;i<=100000;i++) {
            if(isPrime[i]==0) {
                // i是素数，就放入primes数组中
                // 更新primes中素数的数量
                primes[primeNum++] = i;
                System.out.println(i + "-" + i*i);
            }

            for(int j=0;i*primes[j]<=100000;j++) {
                // primes[j]*i的结果是个乘积，这样的数字显然不是素数，所以在isPrimes数组中标注为1
                isPrime[primes[j]*i] = 1;

                // 如果i是primes中某个素数的倍数，就没有必要再计算了，退出算下一个，
                // 例如i=8的时候，其实在之前i=4时就已经计算出8不是素数了
                if(i%primes[j]==0) {
                    break;
                }
            }
        }

        // 经过以上代码，0-100001之间所有素数都放入了primes中
    }

    /**
     * 带压缩的并查集查找(即寻找指定数字的根节点)
     * @param i
     */
    private int find(int i) {
        // 如果执向的是自己，那就是根节点了
        if(fathers[i]==i) {
            return i;
        }

        // 用递归的方式寻找，并且将整个路径上所有长辈节点的父节点都改成根节点，
        // 例如1的父节点是2，2的父节点是3，3的父节点是4，4就是根节点，在这次查找后，1的父节点变成了4，2的父节点也变成了4，3的父节点还是4
        fathers[i] = find(fathers[i]);
        return fathers[i];
    }

    /**
     * 并查集合并，合并后，child会成为parent的子节点
     * @param parent
     * @param child
     */
    private void union(int parent, int child) {
        int parentRoot = find(parent);
        int childRoot = find(child);

        // 如果有共同根节点，就提前返回
        if (parentRoot==childRoot) {
            return;
        }

        // child元素根节点是childRoot，现在将childRoot的父节点从它自己改成了parentRoot，
        // 这就相当于child所在的整棵树都拿给parent的根节点做子树了
        fathers[childRoot] = fathers[parentRoot];

        // 合并后，这个树变大了，新增元素的数量等于被合并的字数元素数量
        rootSetSize[parentRoot] += rootSetSize[childRoot];

        // 更像最大数量
        maxRootSetSize = Math.max(maxRootSetSize, rootSetSize[parentRoot]);
    }

    public int largestComponentSize(int[] nums) {
        // 对数组中的每个数，算出所有质因数，构建map
        for (int i=0;i<nums.length;i++) {
            int cur = nums[i];

            // cur的质因数一定是primes中的一个
            for (int j=0;j<primeNum && primes[j]*primes[j]<=cur;j++) {
                if (cur%primes[j]==0) {
                    map.computeIfAbsent(primes[j], key -> new ArrayList<>()).add(i);

                    // 要从cur中将primes[j]有关的倍数全部剔除，才能检查下一个素数
                    while (cur%primes[j]==0) {
                        cur /= primes[j];
                    }
                }
            }

            // 能走到这里依然不等于1，是因为for循环中的primes[j]*primes[j]<<=cur导致了部分素数没有检查到，
            // 例如6，执行了for循环第一轮后，被2除过，cur等于3，此时j=1,那么primes[j]=3，因此 3*3无法小于cur的3，于是退出for循环，
            // 此时cur等于3，应该是个素数，所以nums[i]就能被此时的cur整除，那么此时的cur就是nums[i]的质因数，也应该放入map
            if (cur>1) {
                map.computeIfAbsent(cur, key -> new ArrayList<>()).add(i);
            }
        }

        fathers = new int[nums.length];
        rootSetSize = new int[nums.length];

        // 至此，map已经准备好了，接下来是并查集的事情，先要初始化数组
        for(int i=0;i< fathers.length;i++) {
            // 这就表示：数字i的父节点是自己
            fathers[i] = i;
            // 这就表示：数字i加上其下所有子节点的数量等于1（因为每个节点父节点都是自己，所以每个节点都没有子节点）
            rootSetSize[i] = 1;
        }

        // 遍历map
        for (int key : map.keySet()) {
            // 每个key都是一个质因数
            // 每个value都是这个质因数对应的数字
            List<Integer> list = map.get(key);

            int size = list.size();

            // 超过1个元素才有必要合并
            if (size>1) {
                // 取第0个元素作为父节点
                int parent = list.get(0);

                // 将其他节点全部作为地0个元素的子节点
                for(int i=1;i<size;i++) {
                    union(parent, list.get(i));
                }
            }
        }

        return maxRootSetSize;
    }
}

• 改动完成，提交试试，如下图，左边是前文的成绩，右边是本次优化后的成绩，从122ms优化到96ms，从超51%优化到超91%，优化效果明显

• 至此，《LeetCode952三部曲》全部完成，如果您正在刷题，希望此系列能给您一些参考

欢迎访问我的GitHub

这里分类和汇总了欣宸的全部原创(含配套源码)：https://github.com/zq2599/blog_demos

欢迎关注博客园：程序员欣宸

学习路上，你不孤单，欣宸原创一路相伴...05086920)