图是否是树 · Graph Valid Tree

［抄题］：

给出 n 个节点，标号分别从 0 到 n - 1 并且给出一个 无向边的列表 (给出每条边的两个顶点), 写一个函数去判断这张｀无向｀图是否是一棵树。

给出n = 5 并且 edges = [[0, 1], [0, 2], [0, 3], [1, 4]], 返回 true.

给出n = 5 并且 edges = [[0, 1], [1, 2], [2, 3], [1, 3], [1, 4]], 返回 false.

[暴力解法]：

时间分析：

空间分析：

［思维问题］：

［一句话思路］：

树中不能有环，两点+老大哥三角成环。遍历所有边并且缩点，一旦出现公共祖先就退出。

［输入量］：空： 正常情况：特大：特小：程序里处理到的特殊情况：异常情况（不合法不合理的输入）：

［画图］：

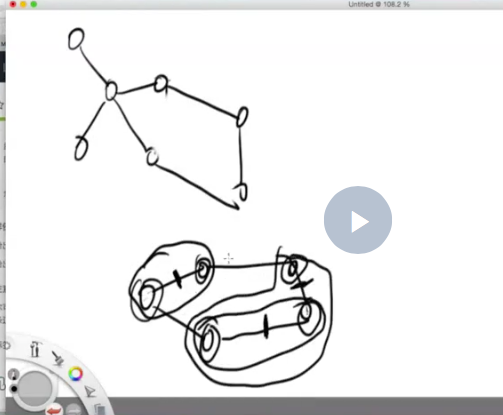
［一刷］：

1. 树的基本性质是: 边= 点数 - 1，若不符合则退出

［二刷］：

［三刷］：

［四刷］：

［五刷］：

[五分钟肉眼debug的结果]：

［总结］：

树中不能有环。

［复杂度］：Time complexity: O(n) Space complexity: O(n)

［英文数据结构或算法，为什么不用别的数据结构或算法］：

两点+老大哥三角成环，union find可以找老大哥。

［关键模板化代码］：

class UnionFind {
        HashMap<Integer, Integer> father = new HashMap<>();

        UnionFind(int n) {
            for (int i = 0; i < n; i++) {
                father.put(i,i);
            }
        }

        int compressed_find(int x) {
            //find ultimate parent
            int parent = x;
            while (parent != father.get(parent)) {
                parent = father.get(parent);
            }
            //change 2 ultimate parent
            int temp = -1;
            int fa = x;
            while (fa != father.get(fa)) {
                temp = father.get(fa);
                father.put(fa,parent);
                fa = temp;
            }
            return parent;
        }

        void union (int x, int y) {
            int fa_x = compressed_find(x);
            int fa_y = compressed_find(y);
            if (fa_x != fa_y) {
                father.put(fa_x,fa_y);
            }
        }
     }

并查集class

［其他解法］：

［Follow Up］：

［LC给出的题目变变变］：

[代码风格] ：

public class Solution {
    /*
     * @param n: An integer
     * @param edges: a list of undirected edges
     * @return: true if it's a valid tree, or false
     */
     //class
     class UnionFind {
        HashMap<Integer, Integer> father = new HashMap<>();

        UnionFind(int n) {
            for (int i = 0; i < n; i++) {
                father.put(i,i);
            }
        }

        int compressed_find(int x) {
            //find ultimate parent
            int parent = x;
            while (parent != father.get(parent)) {
                parent = father.get(parent);
            }
            //change 2 ultimate parent
            int temp = -1;
            int fa = x;
            while (fa != father.get(fa)) {
                temp = father.get(fa);
                father.put(fa,parent);
                fa = temp;
            }
            return parent;
        }

        void union (int x, int y) {
            int fa_x = compressed_find(x);
            int fa_y = compressed_find(y);
            if (fa_x != fa_y) {
                father.put(fa_x,fa_y);
            }
        }
     }

    public boolean validTree(int n, int[][] edges) {
         //corner case is special
        if (edges.length != n - 1) {
            return false;
        }
        UnionFind uf = new UnionFind(n);
        for (int i = 0; i < edges.length; i++) {
            if (uf.compressed_find(edges[i][0]) ==
            uf.compressed_find(edges[i][1])) {
                return false;
            }
            uf.union(edges[i][0], edges[i][1]);
        }
        return true;
    }
}

解法2:

323进化而来

添加每一条边 root1 == root0代表有环，不行

count > 1代表分块，不行

class Solution {
  public boolean validTree(int n, int[][] edges) {
    //use union find
    //ini
    int count = n;
    int[] roots = new int[n];

    //cc
    if (n == 0 || edges == null) return true;

    //initialization the roots as themselves
    for (int i = 0; i < n; i++)
      roots[i] = i;

    //add every edge
    for (int[] edge : edges) {
      int root0 = find(edge[0], roots);
      int root1 = find(edge[1], roots);

        if (root0 == root1) return false;

        //connect but is not merge
        roots[root0] = root1;
        count--;
    }

    //return
    return count == 1;
}

  public int find(int id, int[] roots) {
    while (id != roots[id])
      id = roots[roots[id]];
    return id;
  }
}