Kruscal算法求图的最小生成树

Kruscal算法求图的最小生成树

概述

  和Prim算法求图的最小生成树一样，Kruscal算法求最小生成树也用到了贪心的思想，只不过前者是贪心地选择点，后者是贪心地选择边。而且在算法的实现中，我们还用用到了并查集（也称不相交集的）Union /Find 算法来判断两个节点连通后会不会形成一个环。该算法的思想很简单：将图的所有边按从小到大顺序排序，每次都选取权值最小的边加入最小生成树，如果该边的加入会使生成树形成一个环，则跳过该边。

  这里引入并查集的概念，可以使问题变得简单化。并查集就是利用一个数组sets，如果sets[a]=b，那么我们说a和b在一个生成树（集合）中，且a的双亲是b，如果sets[a]=a,那么我们说a是一个生成树的根。一个图的最小生成树在还没有完全生成前，可能存在多个互不连通的生成树，他们是不相交的集合，我们需要把这些不同的生成树连通起来。

 于是，通过定义一个findroot函数，我们可以找到某顶点的双亲，然后找到该顶点的双亲的双亲，最终找到顶点所在最小生成树的根，例如：如果我们知道sets[a]=b,sets[b]=c,sets[c]=c，那我们可以说a、b、c在同一棵生成树(集合)里，且所在最小生成树的根为c。假设另一个不相交的生成树的根为d，如果我们令sets[c]=d,则将这两个生成树合并为了一个大的生成树，其根为d。

算法图解

1.创建一个9条边，6个顶点的带权无向连通图。



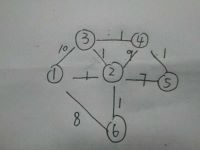
初始状态的并查集如下：



2.将图所有边按权值进行排序。选择权值最小的一条边的两个邻点。为了避免混乱，统一约定该边右边的邻点加入左边的邻点的并查集中，在图中表示为2顶点挂在1顶点下面。





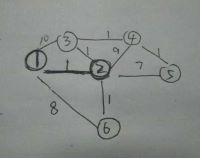
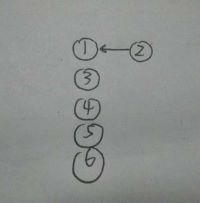
3.就这样，按照权值从小到大不断遍历所有边，都统一把边的大序号的邻点加入小序号的邻点所在的生成树中，3顶点挂在2顶点下面，4顶点挂在3顶点下面，5顶点挂在4顶点下面，6顶点挂在2顶点的下面，最终最小生成树不断长大，且最后所有顶点本质上都挂在1顶点下面，即最小生成树的根为1顶点。





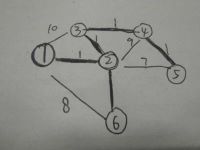
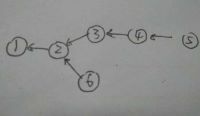
4.最好还剩4条边没有遍历。但我们发现，这4条边的两个邻点都在同一个生成树中了，即他们findroot的结果都是1。如果我们把任意一条边的两个邻点连接起来，都会形成一个环，这是不允许的。故最小生成树的生成就此结束。

代码

1.引入头文件，和之前所讲的的其他图论算法不同的是，这里单独定义一个表示图的边的类，用u，v记录边的邻接点，w记录边的权值。

#include<iostream>
#include<vector>
#include<algorithm>
 //这里同之前我们实现prim算法用的邻接矩阵不同
 //我们用一直特殊的储存方式储存图的边
 using namespace std;

struct edge{
    //边的两个邻点，其中u编号小于v编号
    int u;
    int v;
    //边的权值
    int w;
};

2.定义表示图的类

struct Graph{
    //储存边的容器
    vector<edge> edges;
    //定义并查集,记录各顶点的“根”，确定各顶点是否在同一棵树里
    vector<int> sets;
    //构造函数
    Graph(int vertexnum,int edgenum);
    //析构函数
    ~Graph();
    //kruascal算法的调用接口
    void kruscal();
    //寻根函数，后面会详细讲解其用途
    int findroot(int vertex);
    //按权值给图的边排序的函数
    void sortedges();
};

3.这里自定义一个排序比较函数，后面给储存边的容器排序时会用到。

//排序自定义操作函数
bool cmp(edge a,edge b){
    return a.w<=b.w;
}

4.Graph类的构造函数以及析构函数

Graph::Graph(int vertexnum,int edgenum){
    edges.resize(edgenum+1);
    sets.resize(vertexnum+1);
    //初始化并查集。每个节点相互独立，自己是自己所在生成树的根
    for(int i=1;i<=vertexnum;i++){
        sets[i]=i;
    }
    cout<<"请依次输入各边的两个顶点及其权值"<<endl;
    //注意，为了跟后面寻根函数配合，要保证u定点编号小于v顶点编号
    for(int i=1;i<=edgenum;i++){
        int a,b,w;
        cin>>a>>b>>w;
        if(a>b){
            edges[i].u=a;
            edges[i].v=b;
        }
        else{
            edges[i].v=a;
            edges[i].u=b;
        }
        edges[i].w=w;
    }
}
Graph:: ~Graph(){
    edges.clear();
    sets.clear();
}

5.Kruscal算法的实现。

 //kruascal算法的实现方法
void Graph::kruscal(){
    //调用成员函数对图的所有边进行排序
    sortedges();
    int sum=0;
    for(int i=1;i<=edges.size()-1;i++){
        /*如果该边的两个顶点的根不相同，则让u邻接点成为v邻接点的根的根。
        说形象一点，就是让v邻接点的BOSS归顺于u邻接点的BOSS；
        从而让v归顺于u的BOSS，
        并将该边的权值加入总和中 */
        if(findroot(edges[i].u)!=findroot(edges[i].v)){
            sets[findroot(edges[i].v)]=findroot(edges[i].u);
            //此处非常容易错，读者写代码时一定要仔细
            sum += edges[i].w;
        }
        //否则不进行任何操作
    }
    cout<<"最小生成树的权值和为："<<sum<<endl;
}

6.寻根函数的实现

//利用并查集性质，逐步回溯，找到一个顶点的“根”
 int Graph::findroot(int vertex){
    while(sets[vertex]!=vertex){
        vertex=sets[vertex];
    }
    return vertex;
}

7.对顶点按照权值排序函数的实现

//按权值对顶点进行从小到大排序的函数
void Graph::sortedges(){
    sort(edges.begin(),edges.end(),cmp);
}

8.测试部分。定义一个6个顶点9条边的图，调用接口求该图的最小生成树

int main()
{
    //实例化一个6个顶点，9条边的图对象
    Graph* G=new Graph(6,9);
    //调用接口实现算法
    G->kruscal();
    system("pause");
    return 0;
}

输出

控制台输出结果：