数据挖掘算法——K-means算法

k-means中文称为K均值聚类算法，在1967年就被提出  所谓聚类就是将物理或者抽象对象的集合分组成为由类似的对象组成的多个簇的过程

聚类生成的组成为簇 簇内部任意两个对象之间具有较高的相似度，不同簇的两个对象之间具有较高的相异度

相异度和相似度可以根据描述的对象的属性值来计算  对象间的距离是最常采用的相异度度量指标

常用的距离方法有

k-means是基于划分的方法 就是通过迭代将数据对象划分为k个组每个组为一个簇

每个分组至少包含一个对象

每个对象属于且仅属于某个分组

---

输入：簇的数目K和包含n个对象的数据集D

输出：K个簇的集合

方法：

1.从D中任意选择K个对象作为初始簇的质心；

2.计算每个对象与各簇质心的距离，并且将对象划分到距离其更近的簇

3.更新每个新簇的质心

4.重复2.3步骤，直到簇中的对象不再变化

对K-means算法的几点说明

1.簇的质心就是簇中所有对象在每一维属性的举止组合成的虚拟点 并非实际存在的数据点

2.对噪声和离群（孤立）点数据是敏感，因为它们的存在会对均值的计算产生极大的影响

3.对象到质心的距离通常使用欧式距离来计算

4.要求用户实现给出生成的数目，要求K值已直

5.算法收敛的速度和结果容易受初始质心的影响

来个例子：

数据集：

n = 8, k = 2;取1和3为初始点

序号	属性1	属性2
1	1	1
2	2	1
3	1	2
4	2	2
5	4	3
6	5	3
7	4	4
8	5	4

 #include<bits/stdc++.h>
 using namespace std;
 struct Node
 {
     int id;
     double a, b;
 }node[];
 vector<int>beginn[],endd[];
 int flag = ;
 double distance(pair<double,double>a, Node b){
     return (b.a - a.first) * (b.a - a.first) + (b.b - a.second) * (b.b - a.second);
 }
 bool check(int k )
 {
     if(flag == )
     {
         flag = ;
         return false;
     }
     for(int i =  ; i < k ; i ++)
     {
         if(beginn[i].size() != endd[i].size())
             return false;
         for(int j =  ; j < endd[i].size(); j++)
         {
             if(endd[i][j] != beginn[i][j])
                 return false;
         }
     }
     return true;
 }
 int main()
 {
     int n, k;
     cin >> n >> k;
     for(int i = ; i <= n; i ++)
         cin >> node[i].id >> node[i].a >> node[i].b;
     vector<double>vec[];
     vector< pair<double, double> > gg;
     for(int i = ; i <= k; i ++)
     {
         int x;
         cin >> x;
         gg.push_back(make_pair(node[x].a,node[x].b));
     }//只要把这些点当作是初始点就可以  与其他的点无关即可
     while(true)
     {
         for(int i =  ; i < k; i++)
         {
             beginn[i].assign(endd[i].begin(), endd[i].end());
             endd[i].clear();
         }
         for(int i = ; i < k; i ++) //表示有k个堆 计算每个堆里面的值
         {
             vec[i].clear();
             for(int j = ; j <= n ; j ++)
                 vec[i].push_back(distance(gg[i] , node[j]));//计算的是每个点到初始点的距离
         }
         for(int i =  ;i < n ; i ++)
         {
             double minn = 0x3f3f3f3f;
             int u = -;
             for(int j = ; j < k; j ++){
                 if(vec[j][i] < minn){
                     minn = vec[j][i];
                     u = j;//表示的是哪个簇的
                 }
             }
             endd[u].push_back(i + );
         }
         cout<<"新计算得到的"<<endl;
         for(int i =  ; i < k ; i ++)
         {
             for(int j =  ; j < endd[i].size(); j ++)
                 printf("%d ",endd[i][j]);
             printf("\n");
         }
         cout<<"原本的"<<endl;
         for(int i =  ; i < k ; i ++)
         {
             for(int j =  ; j < beginn[i].size(); j ++)
                 printf("%d ",beginn[i][j]);
             printf("\n");
         }
         gg.clear();
         for(int i =  ; i < k ; i ++)
         {
             double sum1 = , sum2 = ;
             for(int j =  ; j < endd[i].size(); j ++)
             {
                 sum1 += node[endd[i][j]].a;
                 sum2 += node[endd[i][j]].b;
             }
             sum1 = sum1 / endd[i].size();
             sum2 = sum2 / endd[i].size();
             gg.push_back(make_pair(sum1,sum2));     //得到的新的值
         }
         cout<<"新的平均值:"<<endl;
         for(int i =  ; i < k ;i ++)
             cout<<gg[i].first <<"        " << gg[i].second<<endl;
         cout<<endl;
         if(check(k))
             return ;
     }
     return ;
 }

结果可得

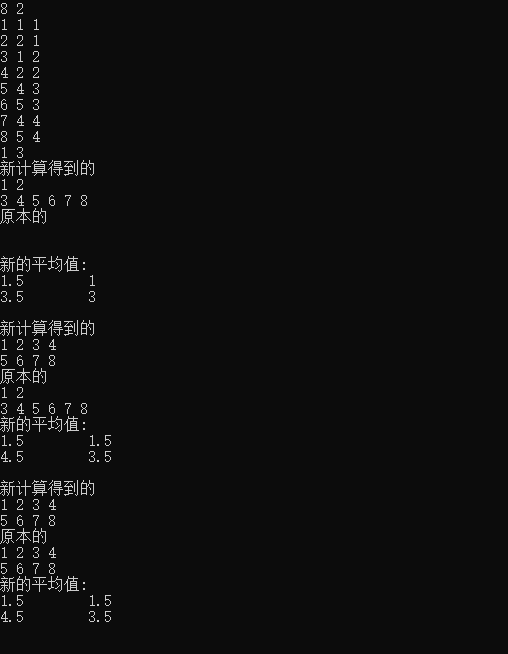
参考来自：

https://www.jianshu.com/p/4f032dccdcef

https://www.icourse163.org/course/CUG-1003556007?utm_campaign=share&utm_medium=androidShare&utm_source=