2019中山纪念中学夏令营-Day20[JZOJ] T1旅游详解

2019中山纪念中学夏令营-Day20[JZOJ]

提高组B组 Team_B组

T1 旅游 Time Limits: 2000 ms  Memory Limits: 262144 KB

Description

ztxz16如愿成为码农之后，整天的生活除了写程序还是写程序，十分苦逼。终于有一天，他意识到自己的生活太过平淡，于是决定外出旅游丰富阅历。

ztxz16生活的城市有N*M个景点，可以描述成一个N*M的矩形，每个景点有一个坐标(x, y) (1 <= x <= N, 1 <= y <= M)以及美观度A[x][y]和观赏所需的时间B[x][y]，从一个景点(x1, y1)走到另一个景点(x2, y2)需要时间为它们之间的曼哈顿距离：|x1 - x2| +|y1 - y2|。

为了防止审美疲劳，ztxz16希望观赏的景点的的美观度是严格上升的，由于不想太早回家码代码，ztxz16希望旅游的总时间尽可能长。

 

Input

第一行输入两个整数N, M；

接下来N行每行M个整数，第x行第y个整数代表A[x][y]；

接下来N行每行M个整数，第x行第y个整数代表B[x][y]；

注意，有一些A[x][y]=B[x][y]=0，说明这个景点已经拆除，不能游览；

Output

输出一行代表最长的总时间。

 

Sample Input

4 5
1 2 6 0 2
1 3 4 0 4
0 0 4 0 3
2 2 0 0 4
1 3 5 0 2
2 8 1 0 2
0 0 3 0 4
0 5 0 0 3

Sample Output

39
【样例说明】
游览顺序为(2,1)->(1,5)->(2,2)->(4,5)->(1,3)
 

 

Data Constraint

对于30%的数据：1<=N<=50 , 1<=M<=50

对于60%的数据：1<=N<=300 , 1<=M<=300

对于100%的数据：1<=N<=1000 , 1<=M<=1000

0<=A[x][y]<=1000000

0<=B[x][y]<=10^9

注意：本题输入数据较大，请注意输入消耗的时间

官方正解：

用f[x][y]表示游览到(x,y)时可能的最长时间，将曼哈顿距离中的绝对值展开后，转移可以表示为四个子矩形中求max的问题，可以使用二维树状数组维护
继续观察发现因为题目要求总长度尽可能长，因此每个点只会在正确的子矩形中贡献最大的答案，因此不需要使用二维树状数组，只需按符号考虑四种情况即可

听说好像要用四边形不等式（反正我也不懂，就瞎搞吧）

我的思路：

先用结构体存矩阵，使其压成一维，然后开始DP乱搞

我们显然可以发现，最优解一定是从上一个观赏度和当前观赏度之差绝对值最小的地方转换过来的

因此可以给DP剪掉一些不可能最优的转移，因为每个点i的bi（即观赏时间）是一定的，我们可以把它从转移式中提出来。

状态转移方程：

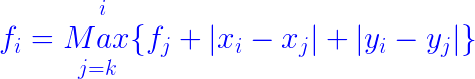
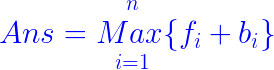
其中：k为上一阶段的观赏度的点排序后的编号（用来剪不必要的转移用的），如果不理解的话可以将j=0，但是会慢很多。

代码实现：

 #include <cstdio>
 #include <algorithm>
 #define rr register
 #define int long long
 using std::sort;
 int n,m,f[*],mark1,mark2,maxn,h[][];
 struct Node{
     int x,y,a,b;
 }node[*];
 bool cmp(Node k,Node l)
 {
     return k.a<l.a;
 }
 int max(int k,int l)
 {
     if(k>l)
         return k;
     return l;
 }
 int abs(int k)
 {
     if(k<)
         return -k;
     return k;
 }
 signed main()
 {
     scanf("%lld %lld",&n,&m);
     int tot=;
     for(rr int i=;i<=n;i++)
         for(rr int j=;j<=m;j++)
         {
             scanf("%lld",&h[i][j]);
         }
         tot=;
     for(rr int i=;i<=n;i++)
         for(rr int j=;j<=m;j++)
         {
             int tmp;
             scanf("%lld",&tmp);
             if(tmp== && h[i][j]==)
                 continue;
             node[tot].a=h[i][j];
             node[tot].b=tmp;
             node[tot].x=i;
             node[tot].y=j;
             tot++;
         }
         tot--;
     sort(node+,node+tot+,cmp);
     for(rr int i=;i<=tot;i++)
     {
         if(node[i].a>node[i-].a)
             {
                 mark2=mark1;
                 mark1=i-;
             }
         if(node[i].a== && node[i].b==)
             continue;

         for(rr int j=max(mark2,);j<i;j++)
         {
             if(node[i].a>node[j].a)
             {
                 if(f[i] < f[j]+abs(node[i].x-node[j].x)+abs(node[i].y-node[j].y))
                     f[i] = f[j]+abs(node[i].x-node[j].x)+abs(node[i].y-node[j].y);
             }
         }
         f[i]+=node[i].b;
         maxn=max(maxn,f[i]);
     }

     printf("%lld",maxn);
 }