SparkMLlib回归算法之决策树

SparkMLlib回归算法之决策树

（一），决策树概念

1，决策树算法（ID3，C4.5 ，CART）之间的比较：

　　1，ID3算法在选择根节点和各内部节点中的分支属性时，采用信息增益作为评价标准。信息增益的缺点是倾向于选择取值较多的属性，在有些情况下这类属性可能不会提供太多有价值的信息。

　　2　ID3算法只能对描述属性为离散型属性的数据集构造决策树，其余两种算法对离散和连续都可以处理

2，C4.5算法实例介绍（参考网址：http://m.blog.csdn.net/article/details?id=44726921）

　　

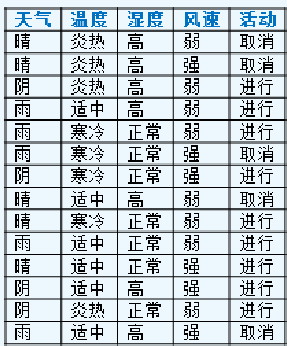
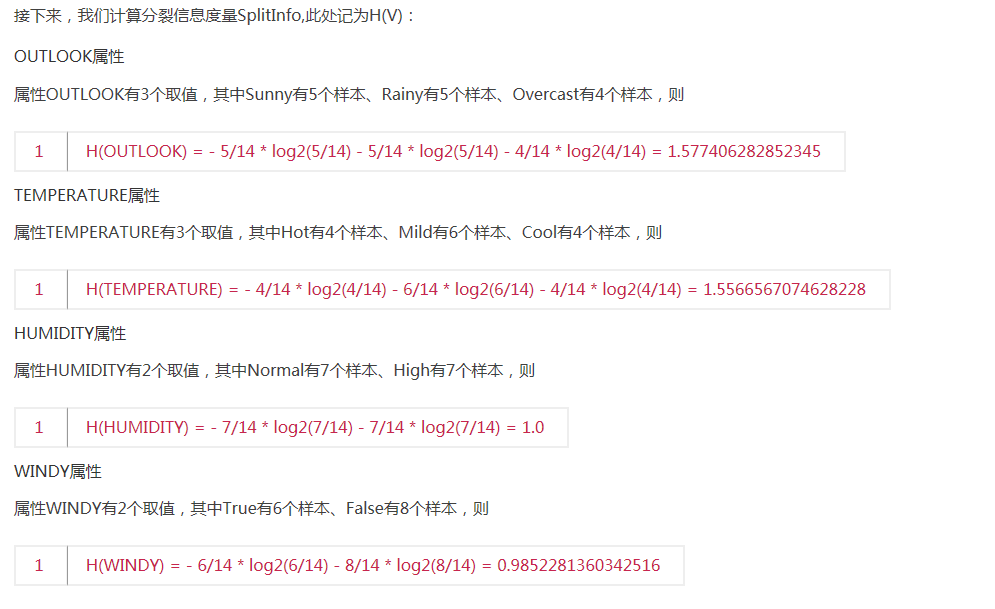
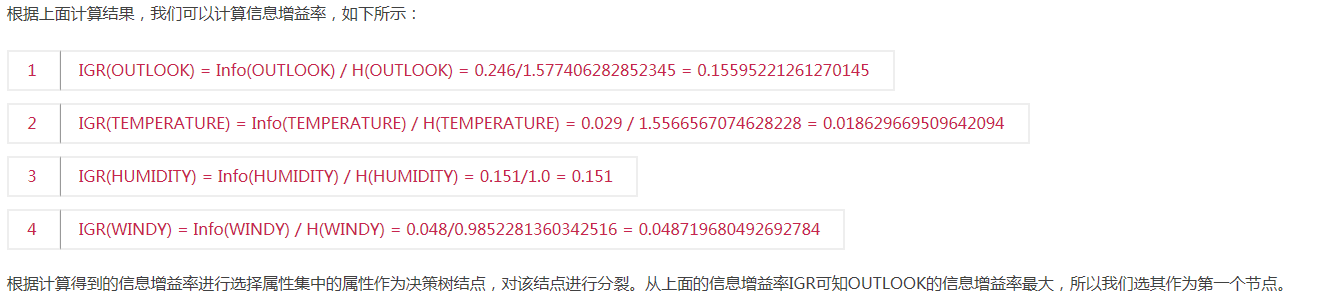
c4.5后剪枝策略：以悲观剪枝为主参考网址：http://www.cnblogs.com/zhangchaoyang/articles/2842490.html

（二） SparkMLlib决策树回归的应用

1，数据集来源及描述：参考http://www.cnblogs.com/ksWorld/p/6891664.html

2，代码实现：

　　2.1 构建输入数据格式：

val file_bike = "hour_nohead.csv"
    val file_tree=sc.textFile(file_bike).map(_.split(",")).map{
      x =>
        val feature=x.slice(2,x.length-3).map(_.toDouble)
        val label=x(x.length-1).toDouble
        LabeledPoint(label,Vectors.dense(feature))
    }
    println(file_tree.first())
   val categoricalFeaturesInfo = Map[Int,Int]()
    val model_DT=DecisionTree.trainRegressor(file_tree,categoricalFeaturesInfo,"variance",5,32)

　　2.2 模型评判标准（mse,mae,rmsle）

val predict_vs_train = file_tree.map {
        point => (model_DT.predict(point.features),point.label)
       /* point => (math.exp(model_DT.predict(point.features)), math.exp(point.label))*/
      }
      predict_vs_train.take(5).foreach(println(_))
      /*MSE是均方误差*/
      val mse = predict_vs_train.map(x => math.pow(x._1 - x._2, 2)).mean()
      /* 平均绝对误差（MAE）*/
      val mae = predict_vs_train.map(x => math.abs(x._1 - x._2)).mean()
      /*均方根对数误差（RMSLE）*/
      val rmsle = math.sqrt(predict_vs_train.map(x => math.pow(math.log(x._1 + 1) - math.log(x._2 + 1), 2)).mean())
      println(s"mse is $mse and mae is $mae and rmsle is $rmsle")
/*
mse is 11611.485999495755 and mae is 71.15018786490428 and rmsle is 0.6251152586960916
*/

（三） 改进模型性能和参数调优

1，改变目标量 （对目标值求根号），修改下面语句

LabeledPoint(math.log(label),Vectors.dense(feature))
和
 val predict_vs_train = file_tree.map {
        /*point => (model_DT.predict(point.features),point.label)*/
        point => (math.exp(model_DT.predict(point.features)), math.exp(point.label))
      }
/*结果
mse is 14781.575988339053 and mae is 76.41310991122032 and rmsle is 0.6405996100717035
*/

决策树在变换后的性能有所下降

2,模型参数调优

　　1,构建训练集和测试集

 val file_tree=sc.textFile(file_bike).map(_.split(",")).map{
      x =>
        val feature=x.slice(2,x.length-3).map(_.toDouble)
        val label=x(x.length-1).toDouble
      LabeledPoint(label,Vectors.dense(feature))
        /*LabeledPoint(math.log(label),Vectors.dense(feature))*/
    }
    val tree_orgin=file_tree.randomSplit(Array(0.8,0.2),11L)
    val tree_train=tree_orgin(0)
    val tree_test=tree_orgin(1)

　　2，调节树的深度参数

val categoricalFeaturesInfo = Map[Int,Int]()
    val model_DT=DecisionTree.trainRegressor(file_tree,categoricalFeaturesInfo,"variance",5,32)
    /*调节树深度次数*/
    val Deep_Results = Seq(1, 2, 3, 4, 5, 10, 20).map { param =>
      val model = DecisionTree.trainRegressor(tree_train, categoricalFeaturesInfo,"variance",param,32)
      val scoreAndLabels = tree_test.map { point =>
        (model.predict(point.features), point.label)
      }
      val rmsle = math.sqrt(scoreAndLabels.map(x => math.pow(math.log(x._1) - math.log(x._2), 2)).mean)
      (s"$param lambda", rmsle)
    }
/*深度的结果输出*/
    Deep_Results.foreach { case (param, rmsl) => println(f"$param, rmsle = ${rmsl}")}
/*
1 lambda, rmsle = 1.0763369409492645
2 lambda, rmsle = 0.9735820606349874
3 lambda, rmsle = 0.8786984993014815
4 lambda, rmsle = 0.8052113493915528
5 lambda, rmsle = 0.7014036913077335
10 lambda, rmsle = 0.44747906135994925
20 lambda, rmsle = 0.4769214752638845
*/

　　深度较大的决策树出现过拟合，从结果来看这个数据集最优的树深度大概在10左右

　　3，调节划分数

/*调节划分数*/
    val ClassNum_Results = Seq(2, 4, 8, 16, 32, 64, 100).map { param =>
      val model = DecisionTree.trainRegressor(tree_train, categoricalFeaturesInfo,"variance",10,param)
      val scoreAndLabels = tree_test.map { point =>
        (model.predict(point.features), point.label)
      }
      val rmsle = math.sqrt(scoreAndLabels.map(x => math.pow(math.log(x._1) - math.log(x._2), 2)).mean)
      (s"$param lambda", rmsle)
    }
    /*划分数的结果输出*/
    ClassNum_Results.foreach { case (param, rmsl) => println(f"$param, rmsle = ${rmsl}")}
/*
2 lambda, rmsle = 1.2995002615220668
4 lambda, rmsle = 0.7682777577495858
8 lambda, rmsle = 0.6615110909041817
16 lambda, rmsle = 0.4981237727958235
32 lambda, rmsle = 0.44747906135994925
64 lambda, rmsle = 0.4487531073836407
100 lambda, rmsle = 0.4487531073836407
*/

　　更多的划分数会使模型变复杂，并且有助于提升特征维度较大的模型性能。划分数到一定程度之后，对性能的提升帮助不大。实际上，由于过拟合的原因会导致测试集的性能变差。可见分类数应在32左右。。