用C实现单隐层神经网络的训练和预测（手写BP算法）
实验要求：
•实现10以内的非负双精度浮点数加法，例如输入4.99和5.70，能够预测输出为10.69
•使用Gprof测试代码热度
代码框架
•随机初始化1000对数值在0~10之间的浮点数，保存在二维数组a[1000][2]中。
•计算各对浮点数的相加结果，保存在数组b[1000]中，即b[0] = a[0][0] + a[0][1]，以此类推。数组a、b即可作为网络的训练样本。
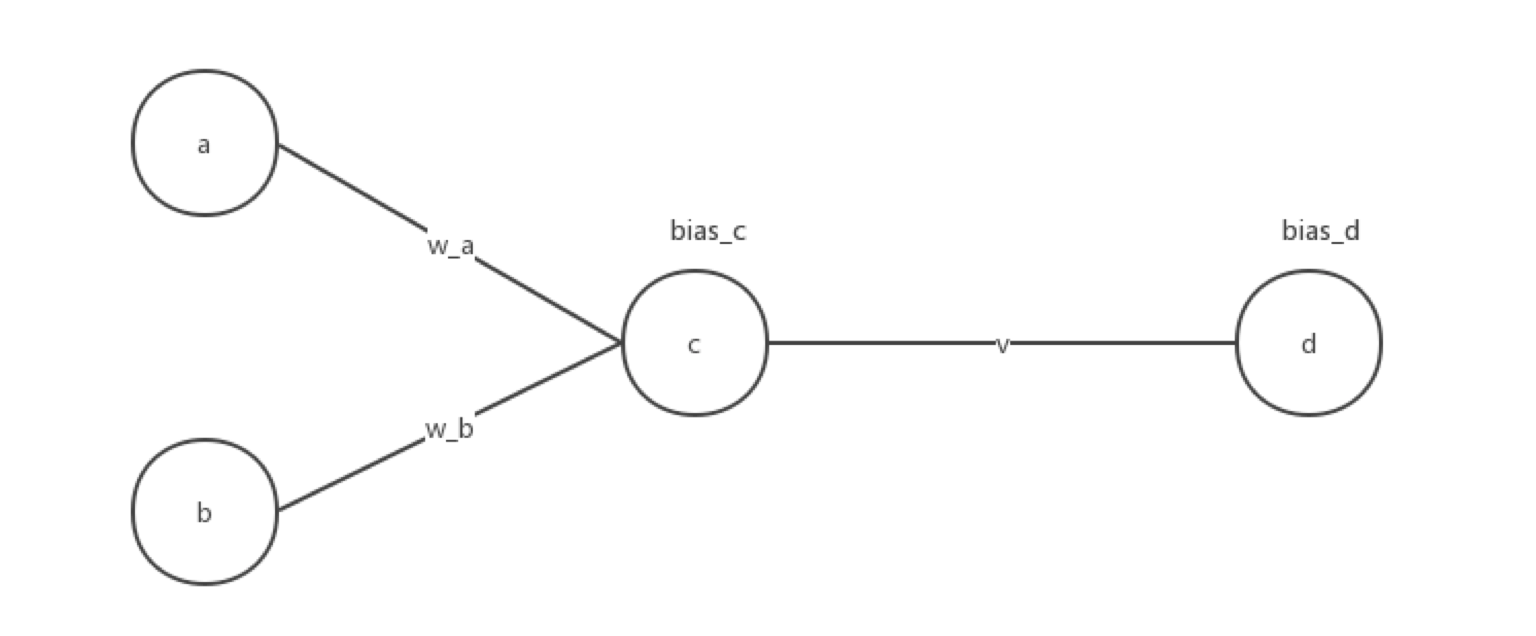
•定义浮点数组w、v分别存放隐层和输出层的权值数据，并随机初始化w、v中元素为-1~1之间的浮点数。
•将1000组输入（a[1000][2]）逐个进行前馈计算，并根据计算的输出结果与b[1000]中对应标签值的差值进行反馈权值更新，调整w、v中各元素的数值。
•1000组输入迭代完成后，随机输入两个浮点数，测试结果。若预测误差较大，则增大训练的迭代次数（训练样本数）。
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
//归一化二维数组
void normalization(float num[][]){
float max1 = 0.0,max2 = 0.0;
float min1 = 0.0,min2 = 0.0;
for(int i = ;i<;i++){
if(num[i][]>max1||num[i][]<min1){
if(num[i][]>max1){
max1 = num[i][];
}
if(num[i][]<min1){
min1 = num[i][];
}
}
if(num[i][]>max2||num[i][]<min2){
if(num[i][]>max2){
max2 = num[i][];
}
if(num[i][]<min2){
min2 = num[i][];
}
}
}
for(int i = ;i<;i++){
num[i][] = (num[i][]-min1+)/(max1-min1+);
num[i][] = (num[i][]-min2+)/(max2-min1+);
}
printf("a[][0]的最大值和最小值分别为：%f\t%f",max1,min1);
printf("\na[][1]的最大值和最小值分别为：%f\t%f",max2,min2);
printf("\n");
}
//归一化一维数组
void normalization_b(float num[]){
float max = 0.0,min = 0.0;
for(int i = ;i<;i++){
if(num[i]>max||num[i]<min){
if(num[i]>max){
max = num[i];
}else{
min = num[i];
}
}
}
for(int i = ;i<;i++){
num[i] = (num[i]-min+)/(max-min+);
}
printf("b数组归一化的最大值和最小值为:%f,%f",max,min);
}
//后向隐藏层公式计算
float compute_hidden(float a,float b,float *w_a,float *w_b,float *bias_c){
float value = 0.0;
value = a*(*w_a)+b*(*w_b)+(*bias_c);
value = /(+exp(-value));
return value;
}
//后向输出层公式计算
float compute_output(float c,float *w_c,float *bias_d){
float value = 0.0;
value = c*(*w_c)+(*bias_d);
value = /(+exp(-value));
return value;
}
//前向输出层公式计算
float pro_output(float predict_num,float real_num){
float error = 0.0;
error = predict_num*(-predict_num)*(real_num-predict_num);
return error;
}
//bp算法
void bp(float a,float b,float real_num,float *w_a,float *w_b,float *v,float *bias_c,float *bias_d){
//前向计算
//隐藏层
float output = compute_hidden(a,b,w_a,w_b,bias_c);
//输出层
float output_final = compute_output(output,v,bias_d);
//反向计算
float error_output = 0.0;
//输出层
error_output = pro_output(output_final,real_num);
//更新权重和偏向！
//定义学习率
double learning_rate = 0.01;
*v = *v + learning_rate*error_output*output;
*bias_d = *bias_d + learning_rate*error_output;
//前向隐藏层
float error_hidden = 0.0;
error_hidden = output*(-output)*(error_output*(*v));
//更新权重和偏向
*w_a = *w_a + learning_rate*(error_hidden*a);
*w_b = *w_b + learning_rate*(error_hidden*b);
*bias_c = *bias_c + learning_rate*error_hidden;
}
int main(int argc, const char * argv[]) {
//随机初始化1000对数值在0-10之间的双精度浮点数，保存在二维数组a[1000][2]中
srand((unsigned) (time(NULL)));
float a[][],b[];
for(int i = ;i<;i++){
for(int j = ;j<;j++){
int rd = rand()%;
a[i][j] = rd/100.0;
}
}
for(int i = ;i<;i++){
b[i] = a[i][] +a[i][];
}
//归一化处理
normalization(a);
normalization_b(b);
//定义浮点数组w,v分别存放隐层和输出层的权值数据，并随机初始化w,v为（-1，1）之间的浮点数
int w_a_rand = rand()%;
int w_b_rand = rand()%;
float w_a = w_a_rand/100000.0-;
float w_b = w_b_rand/100000.0-;
int v_rand = rand()%;
float v = v_rand/100000.0-;
int bias_c_rand = rand()%;
float bias_c = bias_c_rand/100000.0-;
int bias_d_rand = rand()%;
float bias_d = bias_d_rand/100000.0-;
printf("w_a,w_b,v初始随机值分别是:%f %f %f\n",w_a,w_b,v);
//将1000组输入（a[1000][2]）逐个进行前馈计算，并根据计算的输出结果与b[1000]中对应标签值的差值进行反馈权值更新，调整w、v中各元素的数值。
//对于每一个训练实例：执行bp算法
float max1 ,max2 ,min1 ,min2,max,min;
printf("x0的归一化参数（最大最小值):");
scanf("%f,%f",&max1,&min1);
printf("x1的归一化参数（最大最小值):");
scanf("%f,%f",&max2,&min2);
printf("b的归一化参数（最大最小值):");
scanf("%f,%f",&max,&min);
int mark = ;
float trainnig_data_a[][],trainnig_data_b[],test_data_a[][],test_data_b[];
int i = ;
while (i<) {
if(i == mark){
//设置测试集
for(int k = i;k<(i+);k++){
test_data_a[k][] = a[k][];
test_data_a[k][] = a[k][];
test_data_b[k] = b[k];
}
i +=;
}
//设置训练集
if(i<mark){
trainnig_data_a[i][] = a[i][];
trainnig_data_a[i][] = a[i][];
trainnig_data_b[i] = b[i];
i++;
}
if(i>mark){
trainnig_data_a[i-][] = a[i][];
trainnig_data_a[i-][] = a[i][];
trainnig_data_b[i-] = b[i];
i++;
}
}
for(int i = ;i<;i++){
//迭代600次
int times = ;
for(int i= ;i<;i++){
bp(trainnig_data_a[i][],trainnig_data_a[i][],trainnig_data_b[i],&w_a,&w_b,&v,&bias_c,&bias_d);
times++;
}
}
//进行预测
float pre_1,pre_2,predict_value,true_value; float MSE[];
for(int i = ;i<;i++){
pre_1 = test_data_a[i][];
pre_2 = test_data_a[i][];
true_value = test_data_b[i];
//进行计算
float pre_hidden = compute_hidden(pre_1, pre_2, &w_a, &w_b, &bias_c);
predict_value = compute_output(pre_hidden, &v, &bias_d);
//求均方误差
MSE[i] = (predict_value - true_value)*(predict_value-true_value);
predict_value = (predict_value*(max-min+))-+min;
true_value = (true_value*(max-min+))-+min;
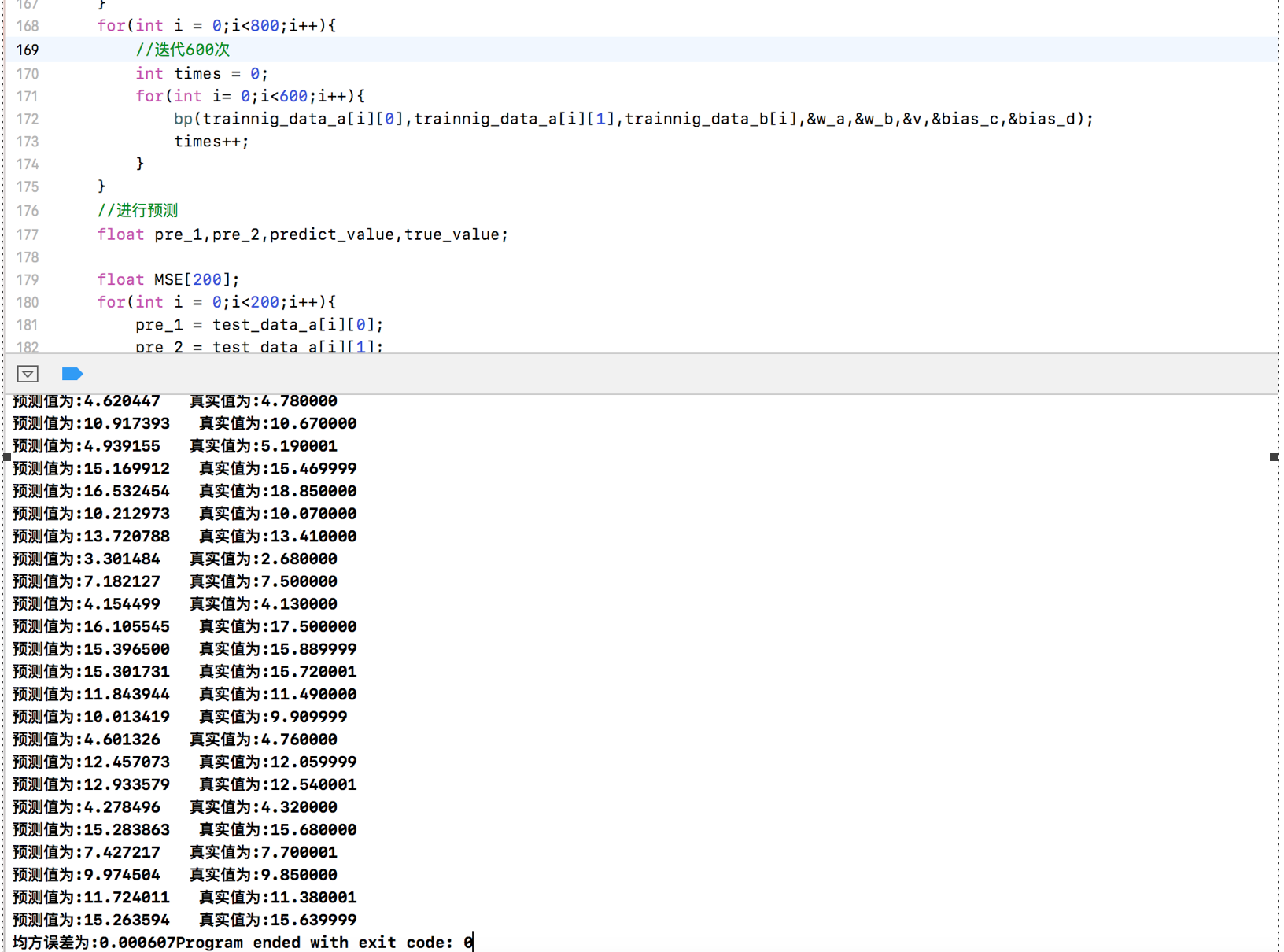
printf("预测值为:%f 真实值为:%f\n",predict_value,true_value);
}
float mean_square_error = ;
for(int i = ;i<;i++){
mean_square_error += MSE[i];
}
mean_square_error = mean_square_error/;
printf("均方误差为:%lf",mean_square_error);
}
运行结果截图：
将隐藏层改为5个神经元
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
struct tag{
float value[];
}x,y;
//归一化二维数组
void normalization(float num[][]){
float max1 = 0.0,max2 = 0.0;
float min1 = 0.0,min2 = 0.0;
for(int i = ;i<;i++){
if(num[i][]>max1||num[i][]<min1){
if(num[i][]>max1){
max1 = num[i][];
}
if(num[i][]<min1){
min1 = num[i][];
}
}
if(num[i][]>max2||num[i][]<min2){
if(num[i][]>max2){
max2 = num[i][];
}
if(num[i][]<min2){
min2 = num[i][];
}
}
}
for(int i = ;i<;i++){
num[i][] = (num[i][]-min1+)/(max1-min1+);
num[i][] = (num[i][]-min2+)/(max2-min1+);
}
printf("a[][0]的最大值和最小值分别为：%f\t%f",max1,min1);
printf("\na[][1]的最大值和最小值分别为：%f\t%f",max2,min2);
printf("\n");
}
//归一化一维数组
void normalization_b(float num[]){
float max = 0.0,min = 0.0;
for(int i = ;i<;i++){
if(num[i]>max||num[i]<min){
if(num[i]>max){
max = num[i];
}else{
min = num[i];
}
}
}
for(int i = ;i<;i++){
num[i] = (num[i]-min+)/(max-min+);
}
printf("b数组归一化的最大值和最小值为:%f,%f",max,min);
}
//后向隐藏层公式计算
struct tag compute_hidden(float a,float b,float *w_a,float *w_b,float *bias_c){
for(int i=;i<;i++){
x.value[i] = a*(w_a[i])+b*(w_b[i])+(bias_c[i]);
x.value[i] = /(+exp(-(x.value[i])));
}
return x;
}
//后向输出层公式计算
float compute_output(struct tag c,float *w_c,float *bias_d){
float value_output = ;
for(int i = ;i<;i++){
c.value[i] = c.value[i]*(w_c[i]);
value_output+=c.value[i];
}
value_output = (value_output+(*bias_d))/;
value_output = /(+exp(-(value_output)));
return value_output;
}
//前向输出层公式计算
float pro_output(float predict_num,float real_num){
float error = 0.0;
error = predict_num*(-predict_num)*(real_num-predict_num);
return error;
}
//bp算法
void bp(float a,float b,float real_num,float *w_a,float *w_b,float *v,float *bias_c,float *bias_d){
//前向计算
//隐藏层
struct tag output = compute_hidden(a,b,w_a,w_b,bias_c);
//输出层
float output_final = compute_output(output,v,bias_d);
//反向计算
float error_output = 0.0;
//输出层
error_output = pro_output(output_final,real_num);
//更新权重和偏向！
//定义学习率
double learning_rate = 0.00003;
for(int i = ;i<;i++){
v[i] = v[i] + learning_rate*error_output*output.value[i];
}
*bias_d = *bias_d + learning_rate*error_output;
//前向隐藏层
float error_hidden[];
for(int i = ;i<;i++){
error_hidden[i] = output.value[i]*(-output.value[i])*(error_output*v[i]);
}
//更新权重和偏向
for(int i = ;i<;i++){
w_a[i] = w_a[i] + learning_rate*(error_hidden[i]*a);
w_b[i] = w_b[i] + learning_rate*(error_hidden[i]*b);
bias_c[i] = bias_c[i] + learning_rate*error_hidden[i];
}
}
int main(int argc, const char * argv[]) {
//随机初始化1000对数值在0-10之间的双精度浮点数，保存在二维数组a[1000][2]中
srand((unsigned) (time(NULL)));
float a[][],b[];
for(int i = ;i<;i++){
for(int j = ;j<;j++){
int rd = rand()%;
a[i][j] = rd/100.0;
}
}
for(int i = ;i<;i++){
b[i] = a[i][] +a[i][];
}
//归一化处理
normalization(a);
normalization_b(b);
//定义浮点数组w,v分别存放隐层和输出层的权值数据，并随机初始化w,v为（-1，1）之间的浮点数
int w_a_rand[];
int w_b_rand[];
for(int i = ;i<;i++){
w_a_rand[i] = rand()%;
}
for(int i = ;i<;i++){
w_b_rand[i] = rand()%;
}
float w_a[];
for(int i = ;i<;i++){
w_a[i] = w_a_rand[i]/100000.0-;
}
float w_b[];
for(int i = ;i<;i++){
w_b[i] = w_b_rand[i]/100000.0-;
}
int v_rand[];
for(int i = ;i<;i++){
v_rand[i] = rand()%;
}
float v[];
for(int i = ;i<;i++){
v[i] = v_rand[i]/100000.0-;
}
int bias_c_rand[];
for(int i = ;i<;i++){
bias_c_rand[i] = rand()%;
}
float bias_c[];
for(int i = ;i<;i++){
bias_c[i] = bias_c_rand[i]/100000.0-;
}
int bias_d_rand = rand()%;
float bias_d = bias_d_rand/100000.0-;
printf("w_a[1-5],w_b[1-5],v[1-5]初始随机值分别是:");
for(int i = ;i<;i++){
printf("w_a[%d]=%f,w_b[%d]=%f,v[%d]=%f\n",i,w_a[i],i,w_b[i],i,v[i]);
}
//将1000组输入（a[1000][2]）逐个进行前馈计算，并根据计算的输出结果与b[1000]中对应标签值的差值进行反馈权值更新，调整w、v中各元素的数值。
//对于每一个训练实例：执行bp算法
float max1 ,max2 ,min1 ,min2,max,min;
printf("x0的归一化参数（最大最小值):");
scanf("%f,%f",&max1,&min1);
printf("x1的归一化参数（最大最小值):");
scanf("%f,%f",&max2,&min2);
printf("b的归一化参数（最大最小值):");
scanf("%f,%f",&max,&min);
int mark = ;
float trainnig_data_a[][],trainnig_data_b[],test_data_a[][],test_data_b[];
int i = ;
while (i<) {
if(i == mark){
//设置测试集
for(int k = i;k<(i+);k++){
test_data_a[k][] = a[k][];
test_data_a[k][] = a[k][];
test_data_b[k] = b[k];
}
i +=;
}
//设置训练集
if(i<mark){
trainnig_data_a[i][] = a[i][];
trainnig_data_a[i][] = a[i][];
trainnig_data_b[i] = b[i];
i++;
}
if(i>mark){
trainnig_data_a[i-][] = a[i][];
trainnig_data_a[i-][] = a[i][];
trainnig_data_b[i-] = b[i];
i++;
}
}
for(int i = ;i<;i++){
//迭代600次
int times = ;
for(int j= ;j<;j++){
bp(trainnig_data_a[i][],trainnig_data_a[i][],trainnig_data_b[i],w_a,w_b,v,bias_c,&bias_d);
times++;
}
}
//进行预测
float pre_1,pre_2,predict_value,true_value; float MSE[];
for(int i = ;i<;i++){
pre_1 = test_data_a[i][];
pre_2 = test_data_a[i][];
true_value = test_data_b[i];
//进行计算
struct tag pre_hidden = compute_hidden(pre_1, pre_2,w_a,w_b,bias_c);
predict_value = compute_output(pre_hidden, v, &bias_d);
//求均方误差
MSE[i] = (predict_value - true_value)*(predict_value-true_value);
predict_value = (predict_value*(max-min+))-+min;
true_value = (true_value*(max-min+))-+min;
printf("预测值为:%f 真实值为:%f\n",predict_value,true_value);
}
float mean_square_error = ;
for(int i = ;i<;i++){
mean_square_error += MSE[i];
}
mean_square_error = mean_square_error/;
printf("均方误差为:%lf",mean_square_error);
}
但结果没什么优化，估计要批量训练可以将结果更优
用C实现单隐层神经网络的训练和预测（手写BP算法）的更多相关文章
- 实现一个单隐层神经网络python
看过首席科学家NG的深度学习公开课很久了,一直没有时间做课后编程题,做完想把思路总结下来,仅仅记录编程主线. 一 引用工具包 import numpy as np import matplotlib. ...
- 吴裕雄 PYTHON 神经网络——TENSORFLOW 单隐藏层自编码器设计处理MNIST手写数字数据集并使用TensorBord描绘神经网络数据
import os import numpy as np import tensorflow as tf import matplotlib.pyplot as plt from tensorflow ...
- Neural Networks and Deep Learning（week3）Planar data classification with one hidden layer(基于单隐藏层神经网络的平面数据分类)
Planar data classification with one hidden layer 你会学习到如何: 用单隐层实现一个二分类神经网络 使用一个非线性激励函数,如 tanh 计算交叉熵的损 ...
- [纯C#实现]基于BP神经网络的中文手写识别算法
效果展示 这不是OCR,有些人可能会觉得这东西会和OCR一样,直接进行整个字的识别就行,然而并不是. OCR是2维像素矩阵的像素数据.而手写识别不一样,手写可以把用户写字的笔画时间顺序,抽象成一个维度 ...
- 可变多隐层神经网络的python实现
说明:这是我对网上代码的改写版本,目的是使它跟前一篇提到的使用方法尽量一致,用起来更直观些. 此神经网络有两个特点: 1.灵活性 非常灵活,隐藏层的数目是可以设置的,隐藏层的激活函数也是可以设置的 2 ...
- python-积卷神经网络全面理解-tensorflow实现手写数字识别
首先,关于神经网络,其实是一个结合很多知识点的一个算法,关于cnn(积卷神经网络)大家需要了解: 下面给出我之前总结的这两个知识点(基于吴恩达的机器学习) 代价函数: 代价函数 代价函数(Cost F ...
- python手写bp神经网络实现人脸性别识别1.0
写在前面:本实验用到的图片均来自google图片,侵删! 实验介绍 用python手写一个简单bp神经网络,实现人脸的性别识别.由于本人的机器配置比较差,所以无法使用网上很红的人脸大数据数据集(如lf ...
- 使用TensorFlow的卷积神经网络识别自己的单个手写数字，填坑总结
折腾了几天,爬了大大小小若干的坑,特记录如下.代码在最后面. 环境: Python3.6.4 + TensorFlow 1.5.1 + Win7 64位 + I5 3570 CPU 方法: 先用MNI ...
- 图片训练：使用卷积神经网络（CNN）识别手写数字
这篇文章中,我们将使用CNN构建一个Tensorflow.js模型来分辨手写的数字.首先,我们通过使之“查看”数以千计的数字图片以及他们对应的标识来训练分辨器.然后我们再通过此模型从未“见到”过的测试 ...
随机推荐
- 将CAGradientLayer用作maskView的遮罩图层
将CAGradientLayer用作maskView的遮罩图层 说明 CAGradientLayer可以用作alpha遮罩,供maskView使用,这两种东西都是非常偏门的东西,但是,偏门不代表功能不 ...
- NSArray排序方法讲解
NSArray排序方法讲解 给数组排序有着多种方式 最麻烦的是sortedArrayUsingSelector:,其次是sortedArrayUsingDescriptors:,最容易使用的就是sor ...
- nodepad++添加新主题
https://www.cnblogs.com/d0main/p/6915460.html
- Linux ip命令详解
ip命令式用来配置网卡ip信息的命令,且是未来的趋势,重启网卡后IP失效 ip常见命令参数 Usage: ip [ OPTIONS ] OBJECT { COMMAND | help } ip [ - ...
- 导出Excel 2007 (NPOI)
今天在导出Excel2007时报了个错,问是否修复,点yes就提示修复正常了,但具体什么原因没说,如图 之前简单的导出代码是这样写的 public static void ExportToWeb(st ...
- CentOS服务器的加固方案
>>>Centos账户安全 对Centos的加固首先要控制用户的权限,用户权限主要涉及到/etc下的/passwd,/shadow和/group三个文件 /passwd文件主要是存储 ...
- Python运算符之三元运算符
三元运算符:也称之为条件表达式 [条件为真的结果] if 条件 else [条件为假的结果] 如: ium01 = 100 if100 > 200 else200 print(num01) #三 ...
- Python 3 实现定义跨模块的全局变量和使用
尽管某些书籍上总是说避免使用全局变量,但是在实际的需求不断变化中,往往定义一个全局变量是最可靠的方法,但是又必须要避免变量名覆盖. Python 中 global 关键字可以定义一个变量为全局变量,但 ...
- Laravel中如何将单个routes.php分割成多个子文件
随着业务逻辑越来越复杂,routes.php文件也会变得越来越庞大,为了便于管理,我们可以像管理配置文件那样将其分割成多个子文件,这实现起来很简单: // app/routes.php ... // ...
- 【洛谷】【st表+模拟】P1311 选择客栈
[题目描述:] 丽江河边有n 家很有特色的客栈,客栈按照其位置顺序从 1 到n 编号.每家客栈都按照某一种色调进行装饰(总共 k 种,用整数 0 ~ k-1 表示),且每家客栈都设有一家咖啡店,每家咖 ...