5.8 NOI 模拟

\(T1\)

比较容易想到的

二分转化为判定,判定是否存在一个子图能保证能一直在\(x\)时间内到达\(n\)

设\(dis(u,v)\)表示\(u->v\)的最短路

先找出候选节点\(i,dis(1,i)+dis(i,n)<=a+x,\)保证一开始出发能到

\(u->v,t+dis(u,v)<=x\)就是说在这个点接到电话能到\(n\)

如果子图有环就合法,否则\(dp,\)只需观察最长时间能否大于等于\(b,\)就是保证这段时间都在子图内

\(T2\)

正解是凸包\(+\)闵可夫斯基和

会吗,不会,我们选择\(KD-Tree\)

#include<bits/stdc++.h>
#define int long long
#define MAXN 110000
using namespace std;
int Ans2=0;
int n,cnt,ls[MAXN],rs[MAXN],col[MAXN],rt;
int Mxx[MAXN],Mxy[MAXN],Mnx[MAXN],Mny[MAXN];
int Mxxcol[MAXN],Mxycol[MAXN],Mnxcol[MAXN],Mnycol[MAXN];
struct node{
    int x,y;
    int col;
}a[MAXN];
void push_up(int now)
{
     if(Mxx[now]<a[cnt].x)
     {
        Mxx[now]=max(Mxx[now],a[cnt].x);
     }
     if(Mxy[now]<a[cnt].y)
     {
        Mxy[now]=max(Mxy[now],a[cnt].y);
     }
     if(Mnx[now]>a[cnt].x)
     {
        Mnx[now]=min(Mnx[now],a[cnt].x);
     }
     if(Mny[now]>a[cnt].y)
     {
        Mny[now]=min(Mny[now],a[cnt].y);
     }
}
int dis(int now)
{
       return (a[cnt].x-a[now].x)*(a[cnt].x-a[now].x)+(a[cnt].y-a[now].y)*(a[cnt].y-a[now].y);
}
int Maxdis(int now)
{
       return max((a[cnt].x-Mxx[now])*(a[cnt].x-Mxx[now]),(Mnx[now]-a[cnt].x)*(Mnx[now]-a[cnt].x))+
              max((a[cnt].y-Mxy[now])*(a[cnt].y-Mxy[now]),(Mny[now]-a[cnt].y)*(Mny[now]-a[cnt].y));
}
bool check(int id,int rt)
{
     if(Mnxcol[rt]==id||Mnycol[rt]==id||Mxxcol[rt]==id||Mxycol[rt]==id) return true;
     return false;
}
void Amax(int now)
{
     if(!now) return ;
     if(a[cnt].col!=col[now]) Ans2=max(Ans2,dis(now));//cout<<cnt<<" "<<col[now]<<"\n";
     int l=Maxdis(ls[now]),r=Maxdis(rs[now]);
     if(l>r)
     {
        if(l>Ans2) Amax(ls[now]);
        if(r>Ans2) Amax(rs[now]);
     }
     else
     {
        if(r>Ans2) Amax(rs[now]);
        if(l>Ans2) Amax(ls[now]);
     }
}
void Ins(int &now,bool opt)
{
     if(!now)
     {
        now=cnt;
        col[now]=a[cnt].col;
        return ;
     }
     if(!opt)
     {
        if(a[cnt].x<=a[now].x)
        {
            Ins(ls[now],1);
        }
        else Ins(rs[now],1);
     }
     else
     {
        if(a[cnt].y<=a[now].y)
        {
            Ins(ls[now],0);
        }
        else Ins(rs[now],0);
     }
     push_up(now);
}
signed main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        scanf("%lld %lld %lld",&a[i].x,&a[i].y,&a[i].col);
    }
    random_shuffle(a+1,a+1+n);
    for(int i=1;i<=n;i++)
    {
        Mxx[i]=Mnx[i]=a[i].x;
        Mxy[i]=Mny[i]=a[i].y;
        col[i]=a[i].col;
        cnt++;
        Amax(rt);
        Ins(rt,0);
    }
    printf("%lld",Ans2);
    return 0;
}

\(T3\)

考场上只得到了一个结论(考场上猜结论这种题一直都不是很会)

\(gcd(s,r)=1\)

打表得到规律得到\(:\)

\(\sum_{i=1}^n\sum_{j=1}^i [gcd(i,j)=1,2\times i<= m,i+j<=n]\)

\(gcd(i,j)=1\)显然

下面证明\(i,j\)的上界我不会证明,可以用运行结果来观察

\(2\times i>m\)会这样

\(n=6,m=6,r=1,s=4\)

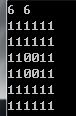
\(i+j>n\)会这样

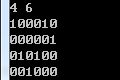
思考一下,我考场上第一个结论(没啥用)想出来,但是第二三个关于上界的,仔细观察一下数据,大胆猜想一下(我想不到),还是说考试时候要多想

题解的做法

令$ a = r + s, b = r − s$

则条件是： \((m<=n,r<=s,a>b)\)

$ gcd(a, b) = 1 $

$ a + b ≤ n$

$ a ≤ m $

$ b < a$

$ a ≡ b(\mod 2)$

和上面那个式子是等价的

令\(ans(n,m)\)表示\((n,m)\)的答案

\(f(n,m)\)表示不考虑\(gcd(a,b)=1\)的答案

\(f'(n,m)\)表示不考虑\(gcd(a,b)=1,a ≡ b(\mod 2)\)的答案