CS229 3.用Normal Equation拟合Liner Regression模型

继续考虑Liner Regression的问题，把它写成如下的矩阵形式，然后即可得到θ的Normal Equation.

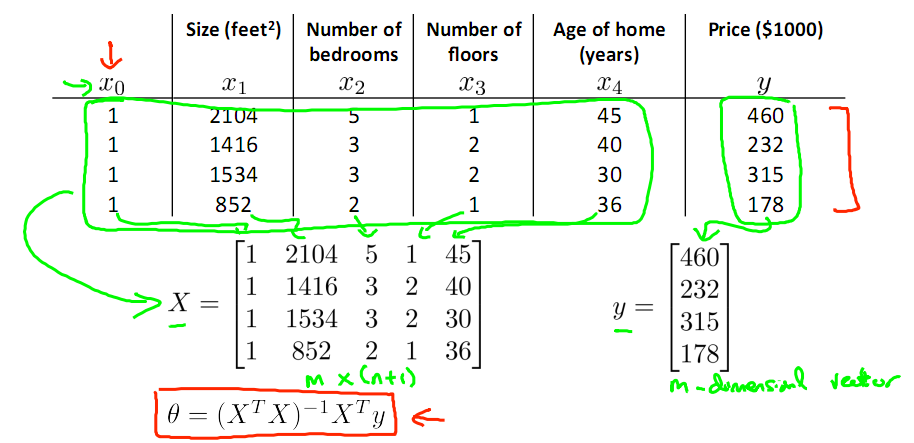
Normal Equation： θ=(X^TX)^-1X^Ty

当X可逆时，(X^TX)^-1X^Ty = X^-1，(X^TX)^-1X^Ty其实就是X的伪逆（Pseudo inverse）。这也对应着Xθ = y ，θ = X^-1y

考虑特殊情况 X^TX 不可逆

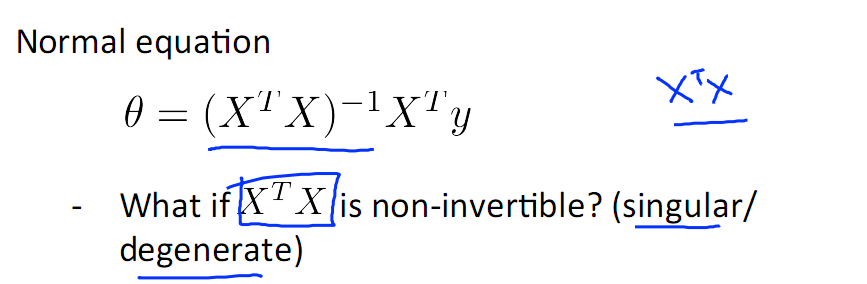
解决办法：

1）考虑是否有冗余的特征，例如特征中有平方米，还有平方厘米，这两个特征就是冗余的，解决办法是去掉冗余

2）再有就是n<<m，其中n 为特征数，m为样本数，比如说用10个样本去学习100个参数的问题，这种情况的解决办法是去feature或者进行Regularization

总结：Gradient descent VS Normal Equation

上图可以看出梯度下降需要选择参数a，并且要多次迭代，有点事特征非常多时，依然正常工作

而Normal Equation 不用选择a，并且不用迭代，只需计算X的伪逆即可，当n很大时，设计到非常大的n×n浮点矩阵运算，当然会很耗时，所以n很大时最好选择Gradient Descent。