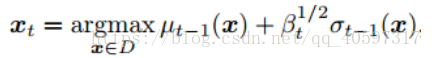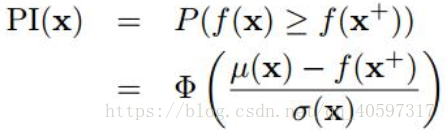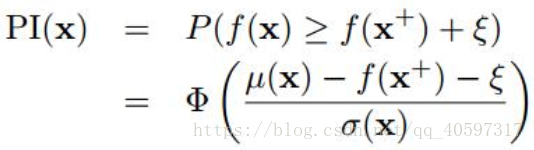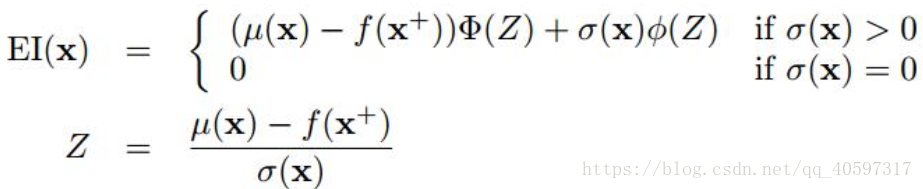贝叶斯优化 Bayesian Optimization
关键字:提取函数aquisition function,熵,响应曲面
简介:所谓优化,实际上就是一个求极值的过程,数据科学的很多时候就是求极值的问题。那么怎么求极值呢?很显然,很容易想到求导数,这是一个好方法,但是求导即基于梯度的优化的条件是函数形式已知才能求出导数,并且函数要是凸函数才可以。然而实际上很多时候是不满足这两个条件的,所以不能用梯度优化,贝叶斯优化应运而生了。
贝叶斯优化常原来解决反演问题,
(反演问题是指由结果及某些一般原理(或模型)出发去确定表征问题特征的参数(或模型参数))
贝叶斯优化的好处在于只需要不断取样,来推测函数的最大值。并且采样的点也不多。
一、贝叶斯优化的适用条件
不知道函数的具体形态即表达式
但是如果给定一个x,可以计算y。这里的计算方法可以使用之前的GPR,如果(x,y)够多了,那么就基本知道函数图像的走势了。
适用于小于20维的空间上优化
二、目的
找出函数的最值,这是最主要的目的。因为很多时候数据科学的一大部分问题都是做非线性函数f(x)的在范围A内的优化,或者简 单的说,求最大值/最小值。比如需要确定拟合的参数,可以求出关于参数的代价函数,求得该代价函数的最小值就可以确定 对应的最优参数了。那么求这个最小值就需要贝叶斯优化了。
大致知道函数长什么样子:与响应曲面相比,贝叶斯只知道最后函数大概什么走向,但是不知道自变量与因变量的关系。可以大致理解为构建响应曲面(虽然响应曲面努力拟合自变量与因变量的关系,下面是关于响应曲面)
响应曲面设计是利用合理的试验设计方法并通过实验得到一定数据,采用多元二次回归方程来拟合与响应值之间的函数关系,通过对回归方程的分析来寻求最优工艺参数,解决多变量问题的一种统计方法。
将响应看作是因素的函数,使用图形技术体现这种函数。一般假设指标和因素之间的关系可以用线性模型表示,即使用多元线性回归的方法。考虑m个因素和n个结果之间的关系,经常使用最小二乘法(就是我们数学上的曲线拟合。注意网页的线性最小二乘法的那一项,很重要。)
对于超定方程组,引入残差平方和函数
三、思路
1.因为GP可以得到在一个新的点x的后验概率P(f(x)|x,D),这里的D为数据集,所以如果想求得极值,可以从GP计算出的x点的均值和方差考虑。可以根据该后验概率的一些指标确定下一个我应该取哪一个点,才有较大的概率尽快的达到极值。
2.如何选取下一个点:求提取函数u达到极值对应的x。这就是上一条的所谓指标。
3.基本算法
可以看出,这里就是不断的求max(AF)对应的点Xt,计算Xt的Yt,即取样,加到数据集。周而复始的循环。
原谅我写的X,Y都是大写,否则x和t一样大了,强迫症发作
关于D,D中的数据周围的方差都较小,也就是我们对他们周围的点了解较多,所以只要有足够多的数据到D里面,那么就会收敛到f(x)
4.Xt的选取
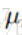
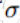
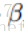
5.优化方向
explore 探索未知的空间,尽可能的探索未知的空间,这样对f(x)的后验概率才会更接近f(x)
exploit,强化已有的结果,在现有最大值的附近进行探索,保证找到的f(x)会更大
6.常用的AF
6.1 probability of improvement(POI)
目的:新的采样能提升最大值的概率最大
表达式为:MPI(maximum probability of improvement),或P算法
Φ(·) 表示的是正态累计分布函数
改进:这里的参数为trade-off系数,可以控制倾向explore还是exploit
这里倾向于局部搜索
6.2 Expected improvement(EI)
可以在explore和explot之间平衡,explore时选择均值大的点,exploit选择方差大的点
参数通常选0.01
6.3 Upper confidence bound
直接比较置信区间的最大值,效果非常好
参考:http://blog.sina.com.cn/s/blog_76d02ce90102xqs6.html
贝叶斯优化 Bayesian Optimization的更多相关文章
- 贝叶斯优化(Bayesian Optimization)深入理解
目前在研究Automated Machine Learning,其中有一个子领域是实现网络超参数自动化搜索,而常见的搜索方法有Grid Search.Random Search以及贝叶斯优化搜索.前两 ...
- 贝叶斯优化(Bayesian Optimization)只需要看这一篇就够了,算法到python实现
贝叶斯优化 (BayesianOptimization) 1 问题提出 神经网咯是有许多超参数决定的,例如网络深度,学习率,正则等等.如何寻找最好的超参数组合,是一个老人靠经验,新人靠运气的任务. 穷 ...
- 基于贝叶斯优化的超参数tuning
https://arimo.com/data-science/2016/bayesian-optimization-hyperparameter-tuning/ 贝叶斯优化:使用高斯过程作为代理函数, ...
- DeepMind提出新型超参数最优化方法:性能超越手动调参和贝叶斯优化
DeepMind提出新型超参数最优化方法:性能超越手动调参和贝叶斯优化 2017年11月29日 06:40:37 机器之心V 阅读数 2183 版权声明:本文为博主原创文章,遵循CC 4.0 BY ...
- 朴素贝叶斯(Naive Bayesian)
简介 Naive Bayesian算法 也叫朴素贝叶斯算法(或者称为傻瓜式贝叶斯分类) 朴素(傻瓜):特征条件独立假设 贝叶斯:基于贝叶斯定理 这个算法确实十分朴素(傻瓜),属于监督学习,它是一个常用 ...
- 调参贝叶斯优化(BayesianOptimization)
from sklearn.datasets import make_classification from sklearn.model_selection import cross_val_score ...
- (ZT)算法杂货铺——分类算法之贝叶斯网络(Bayesian networks)
https://www.cnblogs.com/leoo2sk/archive/2010/09/18/bayes-network.html 2.1.摘要 在上一篇文章中我们讨论了朴素贝叶斯分类.朴素贝 ...
- 条件独立(conditional independence) 结合贝叶斯网络(Bayesian network) 概率有向图 (PRML8.2总结)
本文会利用到上篇,博客的分解定理,需要的可以查找上篇博客 D-separation对任何用有向图表示的概率模型都成立,无论随机变量是离散还是连续,还是两者的结合. 部分图为手写,由于本人字很丑,望见谅 ...
- 条件独立(conditional independence) 结合贝叶斯网络(Bayesian network) 概率有向图 (PRML8.2总结)
转:http://www.cnblogs.com/Dzhouqi/p/3204481.html本文会利用到上篇,博客的分解定理,需要的可以查找上篇博客 D-separation对任何用有向图表示的概率 ...
随机推荐
- iOS-VideoToolbox硬编码H264
前言 VideoToolBox是iOS8之后,苹果开发的用于硬解码编码H264/H265(iOS11以后支持)的API. 对于H264还不了解的童鞋一定要先看下这边的H264的简介. 编码流程 我们实 ...
- 定位ScheduledExecutorService过了一段时间不执行问题
今天查看生产环境的sentinel控制台,发现某dubbo应用一共5个节点,有3个失联了. 查看失联节点的应用日志,服务没有挂,各dubbo接口的日志正常在打印. 在应用节点ping/telnet s ...
- C11中的Unicode
在C11(ISO/IEC 9899:2011)标准中引入了对UTF8.UTF16以及UTF32字符编码的支持. 其中,UTF8字符直接通过char来定义,字面量前缀使用u8.比如: char c = ...
- 004-jdk-数据结构-ArrayList、LinkedList
一.ArrayList概述 数组集合,无容量限制,非线程安全 ArrayList.Vector是线性表,使用Object数组作为容器去存储数据的,添加了很多方法维护这个数组,使其容量可以动态增长,极大 ...
- php-fpm 重启
查看php-fpm进程数:ps aux | grep -c php-fpm [root@ssy106c14c190c69 etc]# ps -ef | grep php-fpm --- 查看php- ...
- SparkMLLib的简单学习
一. 简介 1. 机器学习中,可以将数据划分为连续数据和离散数据 a. 连续数据:可以取任何值,如房价 b. 离散数据:仅有少量特殊值,如一个房屋有2个或3个房间,但不能为2.75个房间 二. 创建向 ...
- Ubuntu 14.04安装Python3
1.添加源 sudo add-apt-repository ppa:fkrull/deadsnakes 2.更新 & 安装 sudo apt-get update sudo apt- pyth ...
- Flutter中的基础组件之一
一.Text文本组件(单一格式的文本) 是具有单一风格的文本字符串,可以跨多行显示,也可全部显示在同一行中,具体显示样子,取决于布局约束. 常用属性: 1.overflow : TextOverflo ...
- mysql写存储过程根据时间变化增加工龄
在工作中遇到要程序根据时间自动增加工龄的需求. php没办法自己发起请求,又不想在服务器上写计划任务crontab,通过用户请求来更改又不能保证用户会去操作. 用数据库的存储过程和事件来完成. 数据库 ...
- mysql/mariadb数据库在插入表数据时,ID竟然成奇数增加了?看完下面内容就知道怎么处理了。
今天突然被问到一个问题,mysql数据库插入表数据时,设置了ID自增,但是插入数据后,ID却呈奇数增加,不是123456类型,而是13579形式,突然有点懵,研究了一会,发现是auto_increme ...