hdu2588 GCD （欧拉函数）

GCD

题意：输入N,M(2<=N<=1000000000, 1<=M<=N), 设1<=X<=N，求使gcd(X,N)>=M的X的个数。  （文末有题）

知识点:   欧拉函数。http://www.cnblogs.com/shentr/p/5317442.html

题解一：

当M==1时，显然答案为N。

当M!=1。  X是N的因子的倍数是 gcd(X,N)>1 && X<=N 的充要条件。so  先把N素因子分解，

N=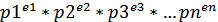          (e1,e2,…en 从0~ei的全排列包含了所有N的因子。)（可能表达不清，看下面。。）

（）中内容相当于：

for(int i=0;i<e1;i++)

for(int j=0;j<e2;j++)

…

for(int k=0;k<en;k++)

x=p1^i*p2^j…pn^k

用dfs解决这个问题，得到所有N的因子。

假设N=p*d,X=q*d.若n与x的最大公约数为d，则能够推出p与q肯定是互质的，因为X<=N所以要求的就是p的欧拉函数值了，那么我们就转化成求满足：N=p*d,并且d>=N的p的欧拉函数值之和了。

如果dfs不是用的很溜的看解法二。

//解法1:

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long LL;
const int N=1e5;

bool vis[N];
int prime[N],cnt;
void is_prime()
{
    cnt=0;
    memset(vis,0,sizeof(vis));
    for(int i=2; i<N; i++)
    {
        if(!vis[i])
        {
            prime[cnt++]=i;
            for(int j=i+i; j<N; j+=i)
                vis[j]=1;
        }
    }
}

int e[100],p[100],cnt2=0;
void fenjie(int n)
{
    cnt2=0;
    memset(e,0,sizeof(e));
    for(int i=0; i<cnt&&prime[i]<=n; i++)
    {
        if(n%prime[i]==0)
        {
            p[cnt2]=prime[i];
            e[cnt2]++;
            n/=prime[i];
            while(n%prime[i]==0)
            {
                n/=prime[i];
                e[cnt2]++;
            }
            cnt2++;
        }
    }
}

int Euler(int n)
{
    int ans=n;
    for(int i=0; i<cnt&&prime[i]<=n; i++)
    {
        if(n%prime[i]==0)
        {
            ans=ans-ans/prime[i];
            while(n%prime[i]==0)
                n/=prime[i];
        }
    }
    if(n==1)
        return ans;
    if(n>1)
        return ans-ans/n;

}

LL dfsans[N],cnt3=0;
void dfs(int cur,LL x)
{
    if(cur==cnt2)
    {
        dfsans[cnt3++]=x;
        return;
    }
    for(int i=0;i<=e[cur];i++)
    {
        LL ans=1;
        for(int j=0;j<i;j++)
            ans*=p[cur];
        dfs(cur+1,x*ans);
    }
}

int main()
{
    int t;
    cin>>t;
    is_prime();
    while(t--)
    {
        LL n,m;
        cin>>n>>m;
        fenjie(n);
        LL ans=0; cnt3=0;
        dfs(0,1);
        for(int i=0;i<cnt3;i++)
        {
            //cout<<dfsans[i]<<endl;
            if(dfsans[i]>=m)
                ans+=Euler(n/dfsans[i]);
        }
        cout<<ans<<endl;
    }
}

题解二：

只是把dfs换了，其他思路和上面一样。

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long LL;
const int N=1e5;

bool vis[N];
int prime[N],cnt;
void is_prime()
{
  	 cnt=0;
   	 memset(vis,0,sizeof(vis));
   	 for(int i=2;i<N;i++)
   	 {
        if(!vis[i])
        {
            prime[cnt++]=i;
            for(int j=i+i;j<N;j+=i)
                vis[j]=1;
       }
    }
}

int e[100],p[100],cnt2=0;
void fenjie(int n)
{
    cnt2=0;
    memset(e,0,sizeof(e));
    for(int i=0;i<cnt&&prime[i]<=n;i++)
    {
        if(n%prime[i]==0)
        {
            p[cnt2]=prime[i];
            e[cnt2]++;
            n/=prime[i];
            while(n%prime[i]==0)
            {
                n/=prime[i];
                e[cnt2]++;
            }
            cnt2++;
        }
    }
}

int Euler(int n)
{
    int ans=n;
    for(int i=0;i<cnt&&prime[i]<=n;i++)
    {
        if(n%prime[i]==0)
        {
            ans=ans-ans/prime[i];
            while(n%prime[i]==0)
                n/=prime[i];
        }
    }
    if(n==1)
        return ans;
    if(n>1)
        return ans-ans/n;

}

/*LL dfsans[N],cnt3=0;
void dfs(int cur,LL x){     if(cur==cnt2)     {         dfsans[cnt3++]=x;          return;     }     for(int i=0;i<=e[cur];i++)    {         LL ans=1;        for(int j=0;j<i;j++)        ans*=p[cur];        dfs(cur+1,x*ans);     } } */

int main()
{
    int t;
    cin>>t;
    is_prime();
    while(t--)
    {
        LL n,m;
        cin>>n>>m;
        fenjie(n);
        LL ans=0;
        /*for(int i=0;i<N;i++)
            dfsans[i]=1;
        cnt3=0;
        dfs(0);
        for(int i=0;i<cnt3;i++)
        {
            cout<<dfsans[i]<<endl;
            if(dfsans[i]>=m)
                ans+=Euler(n/dfsans[i]);
        }*/
        for(int i=1;i*i<=n;i++)
        {
            if(n%i==0)
            {
                if(i>=m)
                ans+=Euler(n/i);
                if((n/i!=i)&&(n/i>=m))
                    ans+=Euler(i);
            }
        }
        cout<<ans<<endl;
    }
}

GCD

Time Limit:1000MS     Memory Limit:32768KB     64bit IO Format:%I64d & %I64u

Submit Status

Description

The greatest common divisor GCD(a,b) of two positive integers a and b,sometimes written (a,b),is the largest divisor common to a and b,For example,(1,2)=1,(12,18)=6.
(a,b) can be easily found by the Euclidean algorithm. Now Carp is considering a little more difficult problem:
Given integers N and M, how many integer X satisfies 1<=X<=N and (X,N)>=M.

Input

The first line of input is an integer T(T<=100) representing the number of test cases. The following T lines each contains two numbers N and M (2<=N<=1000000000, 1<=M<=N), representing a test case.

Output

For each test case,output the answer on a single line.

Sample Input

3
1 1
10 2
10000 72

Sample Output

1
6
260