洛谷P3831 回家的路

题目背景

SHOI2012 D2T1

题目描述

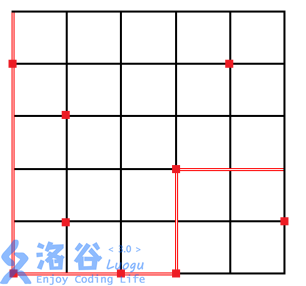
$2046$ 年 $OI$ 城的城市轨道交通建设终于全部竣工，由于前期规划周密，建成后的轨道交通网络由$2n$条地铁线路构成，组成了一个$n$纵$n$横的交通网。如下图所示，这$2n$条线路每条线路都包含$n$个车站，而每个车站都在一组纵横线路的交汇处。

出于建设成本的考虑，并非每个车站都能够进行站内换乘，能够进行站内换乘的地铁站共有$m$个，在下图中，标上方块标记的车站为换乘车站。已知地铁运行 $1$ 站需要 $2$ 分钟，而站内换乘需要步行 $1$ 分钟。$Serenade$ 想要知道，在不中途出站的前提下，他从学校回家最快需要多少时间（等车时间忽略不计）。

输入输出格式

输入格式：

第一行有两个整数$n,m$。

接下去$m$行每行两个整数$x,y$,表示第$x$条横向线路与第$y$条纵向线路的交

汇站是站内换乘站。

接下去一行是四个整数$x_1,y_1,x_2,y_2$。表示 $Serenade$ 从学校回家时，在第 $x_1$条横向线路与第$y_1$条纵向线路的交汇站上车，在第$x_2$条横向线路与第$y_2$条纵向线路的交汇站下车。

输出格式：

输出文件只有一行，即 $Serenade$ 在合理选择线路的情况下，回家所需要的时间。如果 $Serenade$ 无法在不出站换乘的情况下回家，请输出$-1$。

输入输出样例

输入样例#1：

输出样例#1：

输入样例#2：

输出样例#2：

输入样例#3：

输出样例#3：

说明

对于 $30\%$的数据，$n\le 50,m\le 1000$；

对于 $60\%$的数据，$n\le 500,m\le 2000$；

对于 $100\%$的数据，$n\le 20000,m\le 100000$；

思路：

裸的分层最短路，对于这个题目来说，层与层之间的权值为$1$。

而且看数据范围，$n$这么大的一个范围，肯定不能$n^2$存图了，那么我们就枚举每个中转点(换乘点)，横纵分别求两个中转点之间的距离，然后存下来，每层起点和起点的映射及终点和终点的映射都要是0，然后直接上堆优化dijkstra，这个题就做完了。

分层最短路需要注意的问题:

1、数组的大小，这个很重要。

2、确定每层之间的权值是多少。

3、考虑如何建边。

注意了这三个问题之后，分层最短路就跟裸的最短路没什么区别了……

于是我们开开心心的来看代码(代码就不解释了，有了思路就能看懂)：

#include<cstdio>

#include<algorithm>

#include<queue>

#include<cctype>

#include<cstring>

#define maxn 200001

using namespace std;

int num,n,m,head[800001],dis[800001];

inline int qread() {

  char c=getchar();int num=0,f=1;

  for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;

  for(;isdigit(c);c=getchar()) num=num*10+c-'0';return num*f;

}

struct edge {

  int v,w,nxt;

}e[800001];

struct node {

  int x,y;

  bool operator < (const node &a) const {return y>a.y;}

};

struct Edge {

  int x,y,id;

}zrj[maxn];

bool cmp1(Edge a,Edge b){if(a.x==b.x)return a.y<b.y;return a.x<b.x;}

bool cmp2(Edge a,Edge b){if(a.y==b.y)return a.x<b.x;return a.y<b.y;}

inline void ct(int u, int v, int w) {

  e[++num].v=v;

  e[num].w=w;

  e[num].nxt=head[u];

  head[u]=num;

}

priority_queue<node>q;

inline void dijkstra() {

  memset(dis,0x3f,sizeof(dis));

  dis[m+1]=0;q.push((node){m+1,0});

  while(!q.empty()) {

  	int u=q.top().x,d=q.top().y;

  	q.pop();

  	if(d!=dis[u]) continue;

  	for(int i=head[u];i;i=e[i].nxt) {

  	  int v=e[i].v;

	  if(dis[v]>dis[u]+e[i].w) {

	  	dis[v]=dis[u]+e[i].w;

	  	q.push((node){v,dis[v]});

	  }

	}

  }

}

int main() {

  n=qread(),m=qread();

  for(int i=1;i<=m+2;++i) zrj[i].x=qread(),zrj[i].y=qread(),zrj[i].id=i;

  sort(zrj+1,zrj+m+3,cmp1);

  for(int i=1;i<m+2;++i)

  {if(zrj[i].x==zrj[i+1].x) ct(zrj[i].id,zrj[i+1].id,(zrj[i+1].y-zrj[i].y)*2),ct(zrj[i+1].id,zrj[i].id,(zrj[i+1].y-zrj[i].y)*2);}

  sort(zrj+1,zrj+m+3,cmp2);

  for(int i=1;i<m+2;++i)

  {if(zrj[i].y==zrj[i+1].y) ct(zrj[i].id+m+2,zrj[i+1].id+m+2,(zrj[i+1].x-zrj[i].x)*2),ct(zrj[i+1].id+m+2,zrj[i].id+m+2,(zrj[i+1].x-zrj[i].x)*2);}

  for(int i=1;i<=m;++i) ct(i,i+m+2,1),ct(i+m+2,i,1);

  ct(m+1,m*2+3,0),ct(m*2+3,m+1,0);ct(m+2,m*2+4,0),ct(m*2+4,m+2,0);

  dijkstra();

  if(dis[m+2]>1e9) printf("-1\n");

  else printf("%d\n",dis[m+2]);

  return 0;

}

希望这篇题解可以对大家了解分层最短路有些帮助。